Đường tròn có tính đối xứng như thế nào? Giải thích chi tiết kèm ví dụ minh họa Toán 9

Trong chuyên đề Đường tròn lớp 9, một trong những nội dung trọng tâm giúp học sinh hiểu sâu hơn về hình học là tính đối xứng của đường tròn. Hiểu được đường tròn có tính đối xứng như thế nào không chỉ giúp bạn ghi nhớ bản chất của hình tròn mà còn hỗ trợ giải nhanh nhiều bài toán về tiếp tuyến, dây cung, và góc trong đường tròn. Bài viết dưới đây sẽ giải thích chi tiết tính đối xứng của đường tròn, kèm ví dụ minh họa dễ hiểu theo chương trình Toán 9, giúp bạn nắm chắc kiến thức và áp dụng hiệu quả trong học tập.

A. Tính chất đối xứng của đường tròn

Đối xứng tâm

Hai điểm \(H\) và \(K\) gọi là đối xứng với nhau qua điểm \(I\) nếu \(I\) là trung điểm của \(HK\). Điểm \(I\) gọi là tâm đối xứng (Hình 5).

Đối xứng trục

Hai điểm \(H\) và \(K\) gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của \(HK\). Đường thẳng \(d\) gọi là trục đối xứng (Hình 6)

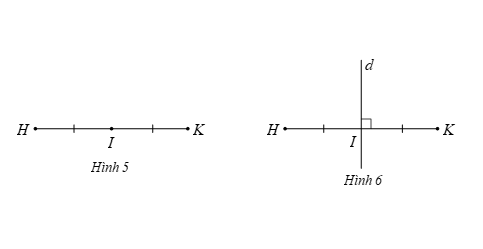
Tâm và trục đối xứng của đường tròn

• Đường tròn là hình có tâm đối xứng, tâm của đường tròn là tâm đối xứng của nó.
• Đường tròn là hình có trục đối xứng, mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó.
• Đường tròn có một tâm đối xứng, nhưng có vô số trục đối xứng.

Ví dụ minh họa về tính chất đối xứng của đường tròn

Ví dụ: Cho đường tròn \((O)\) và hai điểm \(A,\ \ B \in (O)\). Gọi \(d\) là đường trung trực của đoạn \(AB\). Chứng minh rằng \((d)\) là một trục đối xứng của \((O)\).

Hướng dẫn giải

Hình vẽ minh họa:

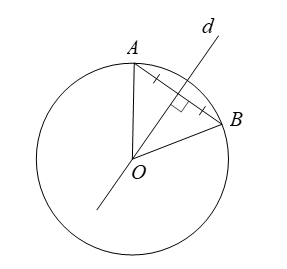
Ta có \(OA = OB = R\) nên \(O\) thuộc đường trung trực của \(AB\)

Mà \(d\) là đường trung trực của \(AB\) nên \(O \in (d)\)

Hay \(d\) đi qua \(O\) nên \(d\) là một trục đối xứng của \((O)\)

Ví dụ: Cho hình vuông \(ABCD\) có \(E\) là giao điểm của hai đường chéo.

a) Chứng minh rằng có một đường tròn đi qua bốn điểm \(A,\ \ B,\ \ C,\ D\). Xác định tâm đối xứng và hai trục đối xứng của đường tròn đó.

b) Tính bán kinh của đường tròn đó nếu hình vuông có cạnh bằng \(3\ cm\).

Hướng dẫn giải

Hình vẽ minh họa:

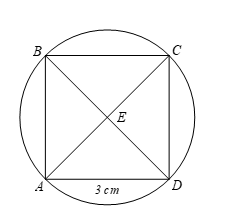
a) Hình vuông \(ABCD\) có \(E\) là giao điểm của hai đường chéo

Nên \(EA = EB = EC = ED\). Vậy bốn điểm \(A,\ \ B,\ \ C,\ \ D\) cùng thuộc đường tròn tâm \(E\), bán kính \(EA\).

\(E\) là tâm đối xứng của đường tròn và \(BD,\ \ AC\) là hai trục đối xứng của đường tròn này.

b) Ta có \(BD^{2} = AB^{2} + AD^{2} = 3^{2} + 3^{2} = 2.\ 3^{2} \Rightarrow BD = 3\sqrt{2}\ cm\)

Như vậy \(BE = \frac{BD}{2} = \frac{3\sqrt{2}}{2} = \frac{3}{\sqrt{2}}\ cm\).

Vậy bán kính của đường tròn tâm \(E\) là \(\frac{3}{\sqrt{2}}\ cm\).

C. Bài tập vận dụng tính chất đối xứng của đường tròn

Bài tập 1: Cho đường tròn \((O)\) và ba điểm \(A,\ \ B,\ \ C\) thuộc đường tròn đó sao cho \(\Delta ABC\) cân tại \(A\).

a) Giả sử \(BC = 6\ cm\), đường cao \(AM\) của \(\Delta ABC\) bằng \(4\ cm\). Tính \(AB\).

b) Gọi \(B'\) là điểm đối xứng với \(B\) qua \(O\). Vẽ \(AH\bot CB'\) tại \(H\). Tứ giác \(AHCM\) là hình gì?

Bài tập 2. Cho hai đường tròn \((O;\ \ R)\) và \((O';\ \ r)\) cắt nhau tại \(A\) và \(B\). Gọi \(M\) là điểm đối xứng với \(A\) qua \(O\), \(N\) là điểm đối xứng với \(A\) qua \(O'\).

a) Chứng minh rằng \(M \in (O)\) và \(N \in (O')\) và ba điểm \(M,\ \ B,\ \ N\) thẳng hàng.

b) Chứng minh rằng đường thẳng \(MN\) tiếp xúc với đường tròn đường kính \(AB\).

Bài tập 3: Cho đường tròn \((O;\ \ R)\) và điểm \(A\) nằm ngoài đường tròn \((O)\). Từ \(A\) kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn \((O)\) ( \(B,\ \ C\) là các tiếp điểm). Gọi \(H\) là giao điểm của \(OA\) và \(BC\).

a) Chứng minh \(A,\ \ B,\ \ C,\ \ O\) cùng thuộc một đường tròn.

b) Chứng minh \(OA\) là đường trung trực của \(BC\).

c) Lấy \(D\) đối xứng với \(B\) qua \(O\). Gọi \(E\) là giao điểm của \(AD\) với đường tròn \((O)\) ( \(E\) không trùng với \(D\)). Chứng minh \(DE.\ BA = BD.\ BE\)

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

------------------------------------------

Qua bài viết trên, bạn đã hiểu rõ đường tròn có tính đối xứng như thế nào và cách vận dụng tính chất đó trong các bài toán Đường tròn Toán 9. Nắm vững tính đối xứng của đường tròn giúp bạn giải nhanh các dạng bài về tiếp tuyến, dây, cung và góc một cách chính xác hơn.