Cách tính diện tích hình vành khăn, hình viên phân
Diện tích hình vành khuyên, diện tích hình viên phân
Hình vành khăn và hình viên phân là hai dạng hình học đặc biệt thường gặp trong chương trình toán học phổ thông, đặc biệt là lớp 9 và các đề thi vào 10. Tuy nhiên, nhiều bạn học sinh vẫn còn nhầm lẫn khi tính diện tích các hình này. Bài viết dưới đây sẽ hướng dẫn bạn cách tính diện tích hình vành khăn, hình viên phân chi tiết, kèm công thức, hình minh họa và ví dụ cụ thể để bạn dễ hiểu và áp dụng chính xác.
A. Công thức tính diện tích hình viên phân
Hình vành khăn là gì?
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là đường tròn đồng tâm)
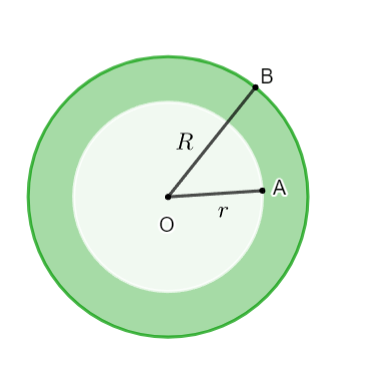
Hình viên phân là gì?
Hình viên phân là phần hình tròn được giới hạn bởi một cung và dây căng cung.
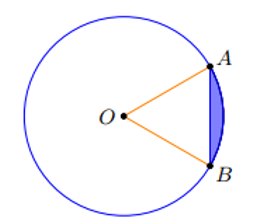
Công thức diện tích hình vành khăn
+ Diện tích ![]() \(S_{q}\) của hình quạt tròn bán kính
\(S_{q}\) của hình quạt tròn bán kính ![]() \(R\) ứng với cung
\(R\) ứng với cung ![]() \(n{^\circ}\) là:
\(n{^\circ}\) là:
![]() \(S_{q} = \frac{n}{360}\pi R^{2} = \frac{l
\cdot R}{2}\) (3)
\(S_{q} = \frac{n}{360}\pi R^{2} = \frac{l
\cdot R}{2}\) (3)
+ Diện tích ![]() \(S_{v}\) của hình vành khuyên được tạo bởi hai đường tròn đồng tâm có bán kính
\(S_{v}\) của hình vành khuyên được tạo bởi hai đường tròn đồng tâm có bán kính ![]() \(R\) và
\(R\) và ![]() \(r\)
\(r\)
![]() \(S_{v} = \pi\left( R^{2} - r^{2}
\right)\) (với
\(S_{v} = \pi\left( R^{2} - r^{2}
\right)\) (với ![]() \(R > r\)) (4)
\(R > r\)) (4)
B. Bài tập tính diện tích hình viên phân, hình vành khăn
Bài 1: Tính diện tích của hình vành khuyên, biết hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là ![]() \(2,5cm\);
\(2,5cm\); ![]() \(2cm\).
\(2cm\).
Hướng dẫn giải
Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính ![]() \(2,5cm\) và
\(2,5cm\) và ![]() \(2cm\) là:
\(2cm\) là:
![]() \(S = \pi\left( R^{2} - r^{2} \right) =
\pi\left( 2,5^{2} - 2^{2} \right) = \frac{9\pi}{4} \approx 7,07\left(
cm^{2} \right)\)
\(S = \pi\left( R^{2} - r^{2} \right) =
\pi\left( 2,5^{2} - 2^{2} \right) = \frac{9\pi}{4} \approx 7,07\left(
cm^{2} \right)\)
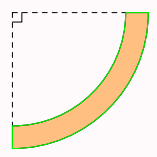
Bài 2: Hình bên mô tả mặt cắt của khúc gỗ có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là ![]() \(4dm\) và
\(4dm\) và ![]() \(3dm\). Diện tích mặt cắt đó là bao nhiêu decimet vuông (làm tròn đến hàng phần mười)?
\(3dm\). Diện tích mặt cắt đó là bao nhiêu decimet vuông (làm tròn đến hàng phần mười)?
Hướng dẫn giải
Hình vẽ minh họa
Diện tích của mặt cắt là: ![]() \(\frac{1}{4}\pi\left( 4^{2} - 3^{2} \right) =
\frac{7\pi}{4} \approx 5,5\left( dm^{2} \right)\)
\(\frac{1}{4}\pi\left( 4^{2} - 3^{2} \right) =
\frac{7\pi}{4} \approx 5,5\left( dm^{2} \right)\)
Bài 3: Cho hình vành khuyên giới hạn bởi hai đường tròn ![]() \((O;r)\) và
\((O;r)\) và ![]() \((O;R)\) với
\((O;R)\) với ![]() \(R
> r\). Trên đường tròn
\(R
> r\). Trên đường tròn ![]() \((O;R)\) lấy hai điểm
\((O;R)\) lấy hai điểm ![]() \(B\),
\(B\), ![]() \(C\) sao cho
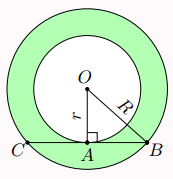
\(C\) sao cho ![]() \(BC\) vừa là dây cung của
\(BC\) vừa là dây cung của ![]() \((O;R)\), vừa vuông góc với bán kính của đường tròn
\((O;R)\), vừa vuông góc với bán kính của đường tròn ![]() \((O;r)\) tại
\((O;r)\) tại ![]() \(A\) (hình vẽ bên)
\(A\) (hình vẽ bên)
a) Tính độ dài đoạn thẳng ![]() \(BC\) theo
\(BC\) theo ![]() \(r\) và
\(r\) và ![]() \(R\).
\(R\).
b) Cho ![]() \(BC = a\sqrt{3}\). Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn
\(BC = a\sqrt{3}\). Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn ![]() \((O;r)\) và
\((O;r)\) và ![]() \((O;R)\) theo
\((O;R)\) theo ![]() \(a\).
\(a\).
Hướng dẫn giải
Hình vẽ minh họa
a) ![]() \(BC = 2AB = 2\sqrt{OB^{2} - OA^{2}} =
2\sqrt{R^{2} - r^{2}}\)
\(BC = 2AB = 2\sqrt{OB^{2} - OA^{2}} =
2\sqrt{R^{2} - r^{2}}\)
b) Diện tích hình vành khuyên giới hạn bởi hai đường tròn ![]() \((O;r)\) và
\((O;r)\) và ![]() \((O;R)\) là:
\((O;R)\) là:
![]() \(S = \pi\left( R^{2} - r^{2} \right) =
\pi\left( \frac{BC}{2} \right)^{2}\)
\(S = \pi\left( R^{2} - r^{2} \right) =
\pi\left( \frac{BC}{2} \right)^{2}\)
![]() \(= \pi\left( \frac{a\sqrt{3}}{2}
\right)^{2} = \frac{3\pi}{4}a^{2}\left( cm^{2} \right)\)
\(= \pi\left( \frac{a\sqrt{3}}{2}
\right)^{2} = \frac{3\pi}{4}a^{2}\left( cm^{2} \right)\)
Bài 4: Phần hình tròn được giới hạn bởi một cung và dây căng cung đó gọi là hình viên phân. Tính diện tích hình viên phân ![]() \(AmB\), biết góc ở tâm
\(AmB\), biết góc ở tâm ![]() \(\widehat{AOB} = 60{^\circ}\) và bán kính đường tròn là
\(\widehat{AOB} = 60{^\circ}\) và bán kính đường tròn là ![]() \(5,1cm\) (hình vẽ bên) (kết quả làm tròn đến hàng phần trăm của
\(5,1cm\) (hình vẽ bên) (kết quả làm tròn đến hàng phần trăm của ![]() \(cm^{2}\)).
\(cm^{2}\)).
Hướng dẫn giải
Hình vẽ minh họa
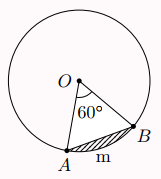
Ta có: ![]() \(OAB\) là tam giác đều cạnh
\(OAB\) là tam giác đều cạnh ![]() \(R\), suy ra:
\(R\), suy ra:
![]() \(S_{OAB} = \frac{R^{2}\sqrt{3}}{4} =
\frac{5,1^{2} \cdot \sqrt{3}}{4} \approx 11,26\left( cm^{2}
\right)\)
\(S_{OAB} = \frac{R^{2}\sqrt{3}}{4} =
\frac{5,1^{2} \cdot \sqrt{3}}{4} \approx 11,26\left( cm^{2}
\right)\)
Bài 5: Cho đường tròn ![]() \((O;R)\) nội tiếp hình vuông
\((O;R)\) nội tiếp hình vuông ![]() \(ABCD\) và ngoại tiếp hình vuông
\(ABCD\) và ngoại tiếp hình vuông ![]() \(MNPQ\). Biết rằng
\(MNPQ\). Biết rằng ![]() \(BD = 12cm\). Tính diện tích phần tô đen.
\(BD = 12cm\). Tính diện tích phần tô đen.
Hướng dẫn giải
Hình vẽ minh họa bài toán:
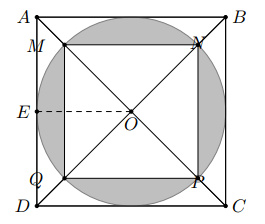
Để tính diện tích phần tô đen, ta chỉ cần tính diện tích hìn viên phân giới hạn bởi cung ![]() \(MQ\) và dây
\(MQ\) và dây ![]() \(MQ\).
\(MQ\).
![]() \(BD = 12cm\) thì
\(BD = 12cm\) thì ![]() \(AB = 6\sqrt{2}cm\);
\(AB = 6\sqrt{2}cm\); ![]() \(OE = 3\sqrt{2}cm\).
\(OE = 3\sqrt{2}cm\).
Diện tích hình quạt ![]() \(OMEQO\) là:
\(OMEQO\) là:
![]() \(S_{1} = \frac{\pi R^{2}n}{360} =
\frac{\pi\left( 3\sqrt{2} \right) \cdot 90}{360} = \frac{9\pi}{2}\left(
cm^{2} \right)\)
\(S_{1} = \frac{\pi R^{2}n}{360} =
\frac{\pi\left( 3\sqrt{2} \right) \cdot 90}{360} = \frac{9\pi}{2}\left(
cm^{2} \right)\)
Diện tích tam giác ![]() \(MOQ\) là:
\(MOQ\) là: ![]() \(S_{2} = \frac{1}{2}OM \cdot OQ = 9\left( cm^{2}
\right)\)
\(S_{2} = \frac{1}{2}OM \cdot OQ = 9\left( cm^{2}
\right)\)
Do đó diện tích hình viên phân giới hạn bởi cung ![]() \(MQ\) và dây
\(MQ\) và dây ![]() \(MQ\) là:
\(MQ\) là:
![]() \(S_{3} = S_{1} - S_{2} = \frac{9\pi}{2} -
9 = \frac{9(\pi - 2)}{2}\left( cm^{2} \right)\)
\(S_{3} = S_{1} - S_{2} = \frac{9\pi}{2} -
9 = \frac{9(\pi - 2)}{2}\left( cm^{2} \right)\)
Vậy diện tích phần tô đen là: ![]() \(S = 4 \cdot
S_{3} = 18(\pi 2)\left( cm^{2} \right)\).
\(S = 4 \cdot
S_{3} = 18(\pi 2)\left( cm^{2} \right)\).
C. Bài tập tự rèn luyện có đáp án hướng dẫn chi tiết
Bài 1: Tính diện tích của hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là ![]() \(3m\) và
\(3m\) và ![]() \(5m\).
\(5m\).
Bài 2: Tính diện tích của hình vành khuyên giới hạn bởi hai đường tròn ![]() \((O;5cm)\) và
\((O;5cm)\) và ![]() \((O;8cm)\) (kết quả làm tròn đến hàng phần trăm).
\((O;8cm)\) (kết quả làm tròn đến hàng phần trăm).
Bài 3: Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn ![]() \((O;10cm)\) và
\((O;10cm)\) và ![]() \((O;20cm)\) (kết quả làm tròn đến hàng phần trăm).
\((O;20cm)\) (kết quả làm tròn đến hàng phần trăm).
Bài 4: Cho lục giác đều ![]() \(ABCDEF\) nội tiếp đường tròn
\(ABCDEF\) nội tiếp đường tròn ![]() \((O;2cm)\). Tính diện tích phần hình tròn nằm bên ngoài hình lục giác.
\((O;2cm)\). Tính diện tích phần hình tròn nằm bên ngoài hình lục giác.
Bài 5: Hình viên phân là hình giới hạn bởi một cung tròn và dây cung (tương ứng) của đường tròn (minh họa bởi phần tô đậm ở hình a). Người ta làm một họa tiết trang trí bằng cách ghép hai hình viên phân bằng nhau (hình b), mỗi hình viên phân đó có góc ở tâm tương ứng là ![]() \(90{^\circ}\) và bán kính đường tròn tương ứng là
\(90{^\circ}\) và bán kính đường tròn tương ứng là ![]() \(2dm\). Tính diện tích của họa tiết trang trí đó (theo đơn vị centimét vuông và làm tròn kết quả đến hàng phần trăm)
\(2dm\). Tính diện tích của họa tiết trang trí đó (theo đơn vị centimét vuông và làm tròn kết quả đến hàng phần trăm)
Bài 6: Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính ![]() \(5cm\),
\(5cm\), ![]() \(10cm\),
\(10cm\), ![]() \(15cm\),
\(15cm\), ![]() \(20cm\) và
\(20cm\) và ![]() \(30cm\). Giả thiết rằng người chơi ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba). Biết rằng xác suất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
\(30cm\). Giả thiết rằng người chơi ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba). Biết rằng xác suất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
--------------------------------------
Hy vọng sau khi đọc bài viết, bạn đã hiểu rõ cách tính diện tích hình vành khăn và hình viên phân, cũng như biết cách vận dụng công thức vào bài tập một cách linh hoạt. Đây là phần kiến thức quan trọng trong hình học lớp 9, vì vậy đừng quên luyện tập thường xuyên để thành thạo hơn. Hãy lưu lại bài viết để tiện ôn tập khi cần thiết nhé!








