VnDoc.com

Cách tính xác suất của biến cố Toán 9

Chuyên đề Toán 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Xác suất của biến cố liên quan đến phép thử

A. Xác suất của biến cố liên quan đến phép thử
B. Bài tập tính xác suất của biến cố
C. Bài tập tự rèn luyện tính xác suất của biến cố

Bài viết dưới đây sẽ giúp bạn nắm vững cách tính xác suất của phép thử Toán 9 một cách đơn giản, dễ hiểu và chính xác. Cùng tìm hiểu các công thức, ví dụ minh họa và mẹo làm bài hiệu quả nhé!

A. Xác suất của biến cố liên quan đến phép thử

1. Phép thử ngẫu nhiên và không gian mẫu

Một hoặc một số hành động thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê được tất cả các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.

Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập hợp tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.

Không gian mẫu của phép thử được kí hiệu là: $\Omega$ $Ω$

2. Kết quả thuận lợi cho biến cố

Cho phép thử T. Xét biến cố E, ở đó việc xảy ra hoặc không xảy ra của E tùy thuộc vào kết quả của phép thử T. Kết quả của phép thử T làm cho biến cố E xảy ra gọi là kết quả thuận lợi cho E.

3. Công thức xác suất của biến cố liên quan đến phép thử

Giả sử rằng các kết quả có thể của phép thử T là đồng khả năng. Khi đó xác suất P(E) của biến cố E bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và số phần tử của tập $\Omega$ $Ω$ :

$P(E) = \frac{n(E)}{n(\Omega)}$ $P (E) = \frac{n (E)}{n (Ω)}$

Trong đó $\Omega$ $Ω$ là không gian mẫu của T, $n (E)$ là số kết quả thuận lợi cho biến cố E và $n(\Omega)$ $n (Ω)$ là số phần tử của không gian mẫu.

4. Cách tính xác suất của một biến cố

Để tính xác suất của một biến cố E ta thực hiện theo các bước sau:

Bước 1: Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu $\Omega$ $Ω$ .
Bước 2: Chứng tỏ các kết quả có thể xảy ra của phép thử là đồng khả năng.
Bước 3: Mô tả các kết quả thuận lợi cho biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4: Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu $\Omega$ $Ω$ .

B. Bài tập tính xác suất của biến cố

Bài 1. Trên mặt phẳng cho năm điểm phân biệt $A, B, C, D, E$ trong đó không có 3 điểm nào thẳng hàng. Hai điểm $A, B$ được tô màu đỏ; ba điểm $C, D, E$ được tô màu xanh. Bạn Châu chọn ra ngẫu nhiên một điểm tô màu đỏ, sau đó chọn ngẫu nhiên một điểm tô màu xanh để nối thành một đoạn thẳng. Tính xác suất của mỗi biến cố $X$ :“ Trong hai điểm được chọn ra có điểm $A$ ”.

Hướng dẫn giải

Không gian mẫu của phép thử là: $\Omega = \left\{ AC;AD;AE;BC;BD;BE \right\}$ $Ω = {A C; A D; A E; B C; B D; B E}$

Không gian mẫu có 6 phần tử.

Các kết quả của phép thử là đồng khả năng.

+ Có 3 kết quả thuận lợi cho biến cố X là $A C; A D; A E$ .

Xác suất của biến cố X là $P(X) = \frac{3}{6} = \frac{1}{2}$ $P (X) = \frac{3}{6} = \frac{1}{2}$ .

Bài 2. Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số 1, 2, 3, ..., 20; hai viên bi khác nhau thì viết hai số khác nhau. Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”. Tính xác suất biến cố: “Số xuất hiện trên viên bi được lấy ra chia 7 dư 1”.

Hướng dẫn giải

Tập hợp các kết quả có thể xảy ra là: $\Omega\ = \ \left\{ 1,\ 2,\ldots,\ 20 \right\}.$ $Ω = {1, 2, \dots, 20} .$

Gọi T: “Số xuất hiện trên viên bi được lấy ra chia 7 dư 1”.

Có 3 kết quả thuận lợi là: 1, 8, 15.

Bài 3. Một túi đựng 5 viên bi có cùng khối lượng và kích thước như nhau, được đánh số $1; 2; 3; 4; 5.$ Xét phép thử: “Lấy ngẫu nhiên hai viên bi từ trong túi” và biến cố A: “Tích của hai số ghi trên hai viên bi lớn hơn 10” Tính xác xuất của biến cố A?

Hướng dẫn giải

Không gian mẫu của phép thử là:

$\Omega = \left\{ (1;2);(1;3);(1;4);(1;5);(2;3);(2;4);(2;5);(3;4);(3;5);(4;5) \right\}$ $Ω = {(1; 2); (1; 3); (1; 4); (1; 5); (2; 3); (2; 4); (2; 5); (3; 4); (3; 5); (4; 5)}$

Không gian mẫu có 11 phần tử.

Có 3 kết quả thuận lợi cho biến cố A là $(3; 4); (3; 5); (4; 5)$ .

Vậy $P(A) = \frac{3}{11}$ $P (A) = \frac{3}{11}$ .

Bài 5. Một hộp có $20$ viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số $1,\ \ 2,\ \ 3....,20$ $1, 2, 3. . . ., 20$ ; hai viên bi khác nhau thì viết hai số khác nhau. Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”. Tính xác suất biến cố: “Số xuất hiện trên viên bi được lấy ra chia $7$ dư $1$ ”.

Hướng dẫn giải

Không gian mẫu của phép thử là:

$\Omega$ $Ω$ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.

Có 3 kết quả thuận lợi là: 1, 8, 15

Vậy $P(T) = \frac{3}{20}$ $P (T) = \frac{3}{20}$ .

Bài 6. Trong túi có 6 quả bóng bàn kích thước và chất liệu như nhau gồm 2 quả màu đỏ, 2 quả màu trắng, 2 quả màu xanh. Không nhìn vào túi mà lấy ra 2 quả bóng. Tính xác suất của biến cố A lấy được ít nhất một quả bóng màu đỏ.

Hướng dẫn giải

Kí hiệu các quả bóng đỏ trắng xanh là Đ₁, Đ₂, X₁, X₂, T₁, T₂

Không gian mẫu:

Ω = {Đ₁Đ₂, X₁X₂, T₁T₂, Đ₁X_1, Đ₁X₂, Đ₂X₁, Đ₂X₂, Đ₁T₁, Đ₁T₂, Đ₂T₁, Đ₂T₂, X₁T₁, X₁T₂, X₂T₁, X₂T₂}

Có 9 kết quả thuận lợi cho biến cố A là: Đ₁Đ₂, Đ₁X_1, Đ₁X₂, Đ₂X₁, Đ₂X₂, Đ₁T₁, Đ₁T₂, Đ₂T₁, Đ₂T₂

P(A) = $\frac{9}{15} = \frac{3}{5}$ $\frac{9}{15} = \frac{3}{5}$

Bài 12. Một bình đựng $12$ quả cầu được đánh số từ $1$ đến $12$ có kích thước và khối lượng như nhau. Chọn ngẫu nhiên một quả cầu. Tính xác suất biến cố $A$ : “Chọn được quả cầu có số chia hết cho $3$ ” là bao nhiêu?

Hướng dẫn giải

Kí hiệu: Quả cầu được đánh số từ $1$ đến $12$ .

Không gian mẫu là $\Omega = \left\{ 1\ \ ;\ \ 2\ \ ;\ \ 3\ \ ;\ \ ...\ \ ;\ \ 11\ \ ;\ \ 12 \right\}$ $Ω = {1; 2; 3; . . .; 11; 12}$ suy ra $n(\Omega) = 12$ $n (Ω) = 12$

Kết quả thuận lợi của biến cố $A$ : “Chọn được quả cầu có số chia hết cho 3” là $\left\{ 3\ \ ;\ \ 6\ \ ;\ \ 9\ \ ;\ \ 12 \right\}$ ${3; 6; 9; 12}$

suy ra $n (A) = 4$

Xác suất của biến cố $A$ là: $P(A) = \frac{4}{12} = \frac{1}{3}$ $P (A) = \frac{4}{12} = \frac{1}{3}$ .

Bài 13. Một bó hoa gồm $3$ bông hoa màu đỏ và $1$ bông hoa màu vàng. Bạn Trúc Linh chọn ngẫu nhiên $2$ bông hoa từ bó hoa đó.

a) Liệt kê các cách chọn mà bạn Trúc Linh thực hiện.

b) Tính xác suất của mỗi biến cố sau:

$R$ : “Trong $2$ bông hoa được chọn, có đúng $1$ bông hoa màu đỏ”;

$T$ : “Trong $2$ bông hoa được chọn, có ít nhất $1$ bông hoa màu đỏ”.

Hướng dẫn giải

a) Các cách chọn có thể có là: đỏ $1$ và vàng, đỏ $2$ và vàng, đỏ $3$ và vàng, đỏ $1$ và đỏ $2$ , đỏ $2$ và đỏ $3$ , đỏ $1$ và đỏ $3$ .

b) Có $3$ kết quả thuận lợi cho biến cố R là: đỏ $1$ và vàng, đỏ $2$ và vàng, đỏ $3$ và vàng.

Vậy $P(R) = \frac{3}{6} = \frac{1}{2}$ $P (R) = \frac{3}{6} = \frac{1}{2}$ .

Có tất cả $4$ kết quả thuận lợi cho biến cố $T$ .

Vậy $P(T) = \frac{4}{6} = \frac{2}{3}$ $P (T) = \frac{4}{6} = \frac{2}{3}$ .

C. Bài tập tự rèn luyện tính xác suất của biến cố

Bài 1. Hình vẽ dưới đây mô tả một đĩa tròn bằng bìa cứng được chia thành $12$ phần bằng nhau và ghi các số $1; 2; 3; . . .; 12$ . Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

Xét phép thử: “Quay đĩa tròn một lần” và biến cố $A :$ “Chiếc kim chỉ vào hình quạt ghi số là số nguyên tố”. Tính xác suất của biến cố $A$ .

Bài 2. Viết ngẫu nhiên một số tự nhiên lẻ có $2$ chữ số. Xét biến cố $A$ : “Số tự nhiên viết ra là bình phương của một số tự nhiên”. Tính xác suất của biến cố A.

Bài 3. Gieo một con xúc xắc cân đối đồng chất và có 6 mặt. Tính xác suất của biến cố gieo được mặt có số chấm là bội của 3.

Bài 4. Hình dưới đây mô tả một đĩa tròn, cân đối bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số $1\ ;\ \ 2\ ;\ \ 3\ ;\ \ 4\ ;\ \ 5\ ;\ \ 6\ ;\ \ 7\ ;\ \ 8$ $1; 2; 3; 4; 5; 6; 7; 8$ . Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.

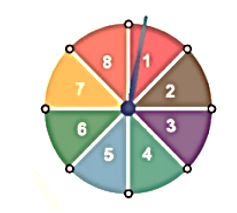
Tính xác suất của các biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của $8$ ”.

Bài 5. Hình bên dưới mô tả một đĩa tròn bằng bìa cứng được chia làm $12$ phần bằng nhau và ghi các số $1, 2, 3, . . ., 12$ ; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

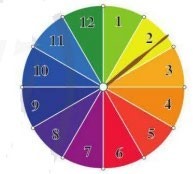
Xét phép thử “Quay đĩa tròn một lần”. Tính xác suất của biến cố D:

a) Chiếc kim chỉ vào hình quạt ghi số nguyên tố.

b) Chiếc kim chỉ vào hình quạt ghi số chia cho 3 dư 1.

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu!

-----------------------------

Trên đây là toàn bộ kiến thức cơ bản và cách tính xác suất của biến cố liên quan đến phép thử Toán lớp 9. Hy vọng qua bài viết này, bạn đã hiểu rõ về tính xác suất và biết cách áp dụng vào bài tập. Đừng quên luyện tập thường xuyên để nâng cao kỹ năng giải toán nhé! Nếu thấy bài viết hữu ích hãy chia sẻ cho bạn bè cùng học nhé!

Chia sẻ, đánh giá bài viết

1

23

Bài trước

Bài sau

Chia sẻ bởi:
Bơ

Tải về

Chọn file muốn tải về:

Cách tính xác suất của biến cố Toán 9

472,6 KB

File Word

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!