Rút gọn biểu thức tỉ số lượng giác của góc nhọn
Ôn tập Toán 9 rút gọn biểu thức lượng giác có đáp án đầy đủ
Trong chương trình Toán 9, chuyên đề Rút gọn biểu thức tỉ số lượng giác của góc nhọn là một trong những dạng toán quan trọng, giúp học sinh củng cố kiến thức về lượng giác cơ bản và rèn luyện kỹ năng biến đổi, tính toán chính xác. Đây cũng là nền tảng cho việc học các chuyên đề nâng cao ở bậc THPT, đặc biệt là hàm số lượng giác và ứng dụng lượng giác trong hình học.
Bài viết này tổng hợp hệ thống bài tập Toán 9 Rút gọn biểu thức có đáp án chi tiết, được biên soạn theo từng mức độ từ cơ bản đến nâng cao. Thông qua đó, học sinh có thể luyện tập nhiều dạng bài khác nhau, nắm chắc phương pháp rút gọn, hạn chế sai sót và nâng cao tư duy logic. Với cách trình bày rõ ràng, lời giải từng bước cụ thể, tài liệu không chỉ giúp học sinh tự học hiệu quả mà còn là nguồn tham khảo hữu ích cho giáo viên khi xây dựng bài giảng và đề kiểm tra.
A. Tỉ số lượng giác của hai góc phụ nhau
Hình vẽ minh họa
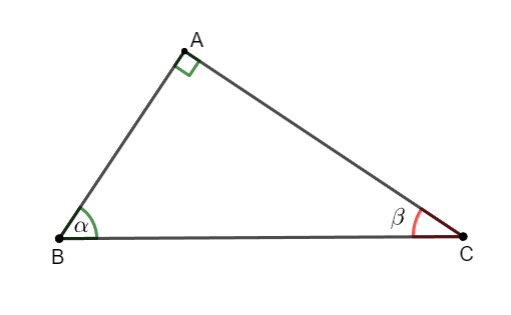
Ta có: 
\(\alpha + \beta =
90^{0}\)
\(\sin\alpha = \cos\beta;cos\alpha =
\sin\beta\)
\(\tan\alpha = \cot\beta;cot\alpha =
\tan\beta\)
B. Bài tập ví dụ minh họa Rút gọn biểu thức tỉ số lượng giác
Bài tập 1. Cho góc nhọn \(\alpha\) thỏa mãn \(0^{\circ} < \alpha <
70^{\circ}\) và biểu thức:
\(A = \tan\alpha \cdot \tan\left( \alpha +
10^{\circ} \right) \cdot \tan\left( \alpha + 20^{\circ} \right) \cdot
\tan\left( 70^{\circ} - \alpha \right) \cdot \tan\left( 80^{\circ} -
\alpha \right) \cdot \tan\left( 90^{\circ} - \alpha \right)\)
Giá trị của biểu thức \(A\) là:
A. 0 B. 1 C. 2 D. 3
Hướng dẫn giải
Ta có:
\(A = \tan\alpha \cdot \tan\left( \alpha +
10^{\circ} \right) \cdot \tan\left( \alpha + 20^{\circ} \right) \cdot
\tan\left( 70^{\circ} - \alpha \right) \cdot \tan\left( 80^{\circ} -
\alpha \right) \cdot \tan\left( 90^{\circ} - \alpha \right)\)
\(A = \left\lbrack
\tan\alpha.tan(90{^\circ} - \alpha) \right\rbrack.\left\lbrack
\tan\left( \alpha + 10^{\circ} \right).tan\left( 80^{\circ} - \alpha
\right) \right\rbrack.\left\lbrack \tan\left( \alpha + 20^{\circ}
\right) \cdot \tan\left( 70^{\circ} - \alpha \right)
\right\rbrack\)
\(A = \left\lbrack \tan\alpha.cot\alpha
\right\rbrack.\left\lbrack \cot(80{^\circ} - \alpha).tan\left(
80^{\circ} - \alpha \right) \right\rbrack.\left\lbrack \tan(70{^\circ} -
\alpha) \cdot \tan\left( 70^{\circ} - \alpha \right)
\right\rbrack\)
\(A = 1\)
Chọn B
Bài tập 2. Rút gọn các biểu thức sau:
| a) \(A = sin23^{\circ} -
cos67^{\circ}\). |
b) \(B = tan18^{\circ}
- cot72^{\circ}\). |
| c) \(C = \frac{sin60^{\circ} \cdot
cos30^{\circ}}{2cot45^{\circ}}\) . |
d) \(D
= cot44^{\circ} \cdot cot45^{\circ} \cdot cot46^{\circ}\). |
| e) \(E = sin10^{\circ} + sin40^{\circ} -
cos50^{\circ} - cos80^{\circ}\). |
f) \(F
= 12 \cdot tan32^{\circ} \cdot tan58^{\circ} - \frac{8 \cdot
cot35^{\circ}}{tan55^{\circ}}\). |
Hướng dẫn giải
a) \(A = sin23^{\circ} -
cos67^{\circ}\)
\(= sin23{^\circ} - \sin(90{^\circ} -
67{^\circ}) = sin23{^\circ} - sin23{^\circ} = 0\).
b) \(B = tan18^{\circ} - cot72^{\circ} =
0\)
c) \(C = \dfrac{\sin60^{\circ} \cdot \cos30^0}{2cot45^{\circ}} =\dfrac{\dfrac{\sqrt{3}}{2}.\dfrac{\sqrt{3}}{2}}{2.1} =\dfrac{3}{8}\)
d) \(D = cot44^{\circ} \cdot cot45^{\circ}
\cdot cot46^{\circ}\)
\(= cot44{^\circ}.1.tan(90{^\circ} -
46{^\circ}) = tan44{^\circ}.cot44{^\circ} = 1\)
e) \(E = sin10^{\circ} + sin40^{\circ} -
cos50^{\circ} - cos80^{\circ}\)
\(= (sin10{^\circ} - cos80{^\circ}) +
(sin40{^\circ} - cos50{^\circ}) = 0\).
f) \(F = 12 \cdot tan32^{\circ} \cdot
tan58^{\circ} - \frac{8 \cdot cot35^{\circ}}{tan55^{\circ}}\)
\(= 12.tan32{^\circ}.cot32{^\circ} -
\frac{8.tan55{^\circ}}{tan55{^\circ}} = 12 - 8 = 4\).
-------------------------------------------
FAQ chuẩn SEO – Rút gọn biểu thức tỉ số lượng giác của góc nhọn
1. Rút gọn biểu thức tỉ số lượng giác của góc nhọn là dạng toán gì?
Đây là dạng toán yêu cầu sử dụng các tỉ số lượng giác của góc nhọn cùng các hệ thức lượng giác để biến đổi biểu thức về dạng đơn giản hơn. Dạng toán này giúp học sinh rèn luyện kỹ năng biến đổi đại số và vận dụng linh hoạt các công thức lượng giác trong tam giác vuông.
2. Muốn rút gọn biểu thức lượng giác của góc nhọn cần ghi nhớ những công thức nào?
3. Những dạng bài rút gọn biểu thức tỉ số lượng giác thường gặp trong Toán 9 là gì?
Một số dạng bài phổ biến gồm:
- Rút gọn biểu thức chỉ chứa sin và cos.
- Rút gọn biểu thức chứa tan và cot.
- Chứng minh hai biểu thức bằng nhau.
- Tính giá trị biểu thức khi biết một tỉ số lượng giác.
- Bài toán kết hợp hệ thức lượng trong tam giác vuông.
4. Khi rút gọn biểu thức lượng giác cần lưu ý điều gì?
Học sinh cần:
- Xác định điều kiện của biểu thức (nếu có).
- Chỉ sử dụng các công thức lượng giác đã được chứng minh.
- Biến đổi từng bước hợp lý, tránh rút gọn tùy ý.
- Giữ nguyên giá trị của biểu thức trong suốt quá trình biến đổi.
--------------------------------------------
Có thể thấy, việc rút gọn biểu thức tỉ số lượng giác của góc nhọn không chỉ là dạng toán thường gặp trong chương trình Toán 9 mà còn là nền tảng quan trọng để học sinh bước vào các chuyên đề lượng giác ở bậc THPT. Thông qua hệ thống bài tập Toán 9 có đáp án chi tiết trong bài viết, các em hoàn toàn có thể tự ôn tập, rèn luyện kỹ năng tính toán nhanh và chính xác, từ đó tự tin hơn trong các kỳ thi.
Hy vọng rằng tài liệu này sẽ là trợ thủ đắc lực giúp học sinh nâng cao năng lực giải toán, đồng thời hỗ trợ giáo viên trong quá trình giảng dạy. Đừng quên luyện tập thường xuyên để nắm chắc phương pháp và đạt kết quả cao trong học tập môn Toán.
