Cách tính diện tích hình tròn, diện tích hình quạt tròn
Diện tích hình tròn, Diện tích hình quạt tròn
Bạn đang tìm cách tính diện tích hình tròn hoặc diện tích hình quạt tròn nhanh chóng và chính xác? Đây là kiến thức cơ bản trong hình học phẳng, thường xuất hiện trong chương trình toán lớp 8, lớp 9 và cả các đề thi. Bài viết sau sẽ hướng dẫn chi tiết công thức, cách áp dụng thực tế kèm ví dụ minh họa dễ hiểu. Cùng khám phá nhé!
A. Công thức tính diện tích hình tròn
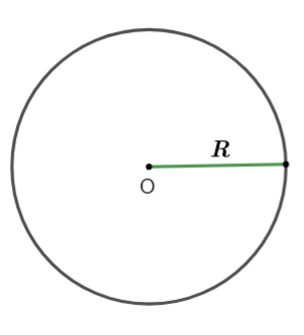
Diện tích hình tròn bán kính 
\(R\) được xác định bằng công thức:
\(S = \pi R^{2}\)
B. Công thức tính diện tích hình quạt tròn
Hình quạt tròn là gì?
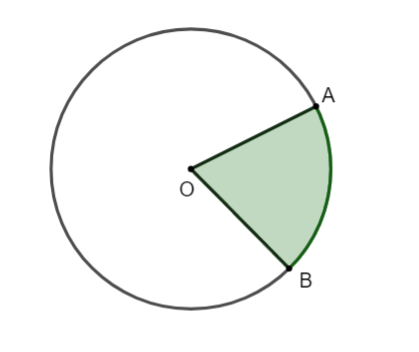
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó.
Công thúc diện tích hình quạt tròn
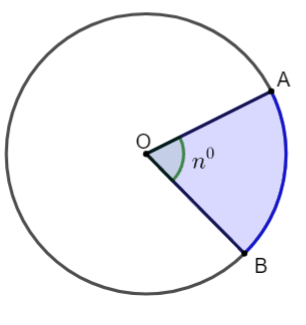
Diện tích \(S_{q}\) của hình quạt tròn bán kính \(R\) ứng với cung \(n{^\circ}\) là:
\(S_{q} = \frac{n}{360}\pi R^{2} = \frac{l
\cdot R}{2}\)
C. Bài tập tính diện tích hình tròn, diện tích hình quạt tròn
Bài 1: a) Tính diện tích hình quạt tròn bán kính \(5(cm)\)
b) Tính diện tích hình quạt tròn bán kính \(6cm\) có số đo cung là \(60{^\circ}\)
Hướng dẫn giải
a) Diện tích hình tòn bán kính \(5\
cm\) là: \(S = \pi R^{2} = 25\pi\left(
cm^{2} \right)\)
b) Diện tích hình quạt tròn là: \(S_{q} =
\frac{\pi R^{2}n}{360} = \frac{\pi \cdot 6^{2} \cdot 60}{360} =
6\pi\left( cm^{2} \right)\)
Bài 2: Bề mặt phía trên của một chiếc trống có dạng hình tròn bán kính \(8cm\). Diện tích bề mặt phía trên của trống đó bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?
Hướng dẫn giải
Diện tích bề mặt phía trên của chiếc trống đó là:
\(S = \pi \cdot 8^{2} = 64\pi \approx 201\
\left( cm^{2} \right)\)
Bài 3: Tính diện tích hình quạt tròn bán kính \(5cm\) và có độ dài cung tương ứng với nó bằng \(4\pi cm\).
Hướng dẫn giải
Theo đề bài, hình quạt tròn có độ dài cung tương ứng với nó là \(l = 4\pi\ (cm)\), bán kính \(R = 5cm\).
Do đó, diện tích \(S\) của nó là:
\(S = \frac{l \cdot R}{2} = \frac{4\pi
\cdot 5}{2} = 10\pi\ \left( cm^{2} \right)\)
D. Bài tập tự rèn luyện tính diện tích hình tròn, hình quạt tròn
Bài 1: Tính diện tích hình quạt tròn bán kính \(R = 10cm\), ứng với cung \(60{^\circ}\) (kết quả làm tròn đến hàng phần trăm của \(cm^{2}\)).
Bài 2: Tính diện tích hình quạt tròn bán kính \(R = 20cm\), ứng với cung \(72{^\circ}\).
Bài 3: Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong hình bên. Biết \(OA = 5cm\) và \(\widehat{AOB} = 55{^\circ}\).
Bài 4: Cho hình quạt tròn \(AOB\) giới hạn bởi hai bán kính \(OA\), \(OB\) và cung \(AmB\) sao cho \(OA = OB\). Hãy tìm số đo cung \(AmB\) ứng với hình quạt tròn đó.
Bài 5: Cho hình quạt tròn \(COD\) giới hạn bởi hai bán kính \(OC\), \(OD\) và cung \(CmD\) sao cho \(OC = OD\). Hãy tìm số đo cung \(CmD\) ứng với hình quạt đó.
Bài 6: Một họa tiết trang trí có dạng hình tròn bán kính \(4dm\) được chia thành nhiều hình quạt tròn, mỗi hình quạt tròn có góc ở tâm là \(7,5{^\circ}\). Diện tích của mỗi hình quạt đó là bao nhiêu \(dm^{2}\) (làm tròn kết quả đến hàng phần trăm)?
Bài 7: Hình quạt ở hình bên có bán kính bằng \(2dm\) và góc ở tâm bằng \(150{^\circ}\)
a) Tính diện tích của hình quạt đó theo đơn vị decimét vuông (làm tròn kết quả đến hàng phần trăm).
b) Tính chiều dài cung tương ứng với hình quạt đó.
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
-----------------------------------------------
Như vậy, bạn đã nắm được cách tính diện tích hình tròn và diện tích hình quạt tròn thông qua các công thức đơn giản, dễ nhớ cùng ví dụ cụ thể. Việc hiểu rõ và vận dụng linh hoạt các kiến thức này sẽ giúp bạn tự tin hơn khi làm bài tập hình học. Đừng quên luyện tập thường xuyên để ghi nhớ lâu hơn nhé!
