Cách tính độ dài đường tròn, độ dài cung tròn
Công thức tính độ dài đường tròn, độ dài cung tròn
Bạn đang tìm hiểu cách tính độ dài đường tròn hoặc độ dài cung tròn? Đây là kiến thức cơ bản nhưng cực kỳ quan trọng trong hình học. Bài viết dưới đây sẽ giúp bạn nắm vững công thức, cách áp dụng, và ví dụ minh họa cụ thể để dễ hiểu và dễ nhớ hơn. Dù bạn là học sinh, sinh viên hay người đang ôn thi, đừng bỏ qua hướng dẫn chi tiết này nhé!
A. Công thức tính độ dài đường tròn
Người ta chứng minh được rằng tỉ số giữa chu vi và đường kính của một đường tròn luôn bằng một số vô tỉ không đổi gọi là 
\(\pi\) (đọc là pi).
Ta có thể tìm được giá trị gần đúng của \(\pi\) nhờ máy tính cầm tay. Trong đời sống, ta thường lấy \(\pi \approx 3,14\).
Do đó, ta có công thức tính độ dài \(C\) của đường tròn \((O;R)\), đường kính \(d = 2R\) là:
\(C = \pi d = 2\pi R\) (1)
B. Công thức tính độ dài cung tròn
Ta có công thức tính độ dài \(l\) của cung \(n{^\circ}\) trên đường tròn \((O;R)\) là:
\(l = \frac{\pi Rn}{180}\) (2)
Nhận xét: Từ hai công thức (1) và (2), ta được: \(l = \frac{n}{360}\pi d = \frac{n}{360} \cdot
C\) hay \(\frac{l}{C} =
\frac{n}{360}\)
Nghĩa là tỉ số giữa độ dài cung \(n{^\circ}\) và độ dài đường tròn (cùng bán kính) đúng bằng \(\frac{n}{360}\).
C. Bài tập tính độ dài đường tròn, độ dài trung tròn
Bài 1: a) Tính chu vi đường tròn biết đường kính là \(5\)cm
b) Tính độ dài cung \(120{^\circ}\) của đường tròn bán kính \(4\)cm.
Hướng dẫn giải
Chu vi đường tròn \(C = 2\pi R =
5\pi\) (cm)
b) Độ dài cung \(120{^\circ}\) của đường tròn bán kính \(4\)cm là:
\(l = \frac{\pi Rn}{180} = \frac{4\pi \cdot
120}{180} = \frac{8\pi}{3}\) (cm)
Bài 2: Tính độ dài cung \(40{^\circ}\) của đường tròn bán kính \(9\)cm.
Hướng dẫn giải
Độ dài cung \(40{^\circ}\) của đường tròn bán kính \(9\)cm là:
\(l = \frac{40}{180} \cdot \pi \cdot 9 =
2\)(cm)
Bài 3: Cho đường tròn \((O;R)\) độ dài cung \(\widehat{AB}\) là \(\frac{\pi R}{4}\). Tính số đo cung \(\widehat{AB}\).
Hướng dẫn giải
Gọi \(n\) là số đó cung nhỏ \(\widehat{AB}\).
Ta có \(l = \frac{\pi Rn}{180} \Rightarrow
\frac{\pi R}{4} = \frac{\pi Rn}{180}\)
\(\Rightarrow n = \frac{180}{4} =
45\)
Do đó số đo cung\(\widehat{AB} =
45{^\circ}\).
Bài 4: Một chất điểm chuyển động trên một đường tròn có bán kính \(r = 0,3\)m với tốc độ không đổi. Chất điểm chuyển động hết một vòng quanh đường tròn đó trong \(20\)s. Tính tốc độ của chất điểm (theo đơn vị mét trên giây và làm tròn kết quả đến hàng phần trăm).
Hướng dẫn giải
Chu vi của đường tròn là \(C = 2\pi \cdot
0,3 = 0,6\pi\) (m)
Vậy tốc độ của chất điểm là \(v =
\frac{0,6\pi}{20} \approx 0,09\) (m/s)
Bài 5: Một con lắc di chuyển từ vị trí \(A\) đến vị trí \(B\). Tính độ dài quãng đường \(AB\) mà con lắc đó đã di chuyển, biết rằng sợi dây \(OA\) có độ dài bằng \(l\) và tia \(OA\) tạo với phương thẳng đứng góc \(\alpha\).
Hướng dẫn giải
Hình vẽ minh họa
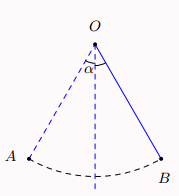
Góc được tạo thành khi con lắc di chuyển từ vị trí \(A\) đến vị trí \(B\) là \(2\alpha\)
Khi đó độ dài quãng đường con lắc đi được là \(AB = \frac{\pi R \cdot 2\alpha}{180} = \frac{\pi
R\alpha}{90}\) (đvđd)
D. Bài tập tự rèn luyện tính độ dài cung tròn, độ dài đường tròn
Bài 1: Tính độ dài cung \(30{^\circ}\) của đường tròn bán kính \(10\)cm.
Bài 2: Tính độ dài cung \(72{^\circ}\) của đường tròn bán kính \(25\)cm. (Lấy \(\pi\) theo máy tính và làm tròn kết quả đến hàng trăm phần trăm)
Bài 3: Cung có số đo \(100{^\circ}\) của đường tròn bán kính \(8\)cm dài bao nhiêu centimét (làm tròn kết quả đến hàng đơn vị)?
Bài 4: Cho \(A\) và \(B\) là hai điểm trên đường tròn \((O;3cm)\) sao cho \(\widehat{AOB} = 120{^\circ}\). Tính số đo và độ dài các cung có hai mút \(A\), \(B\).
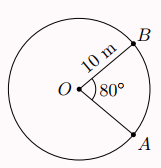
Bài 5: Tính độ dài của đoạn hàng rào từ \(A\) đến \(B\) của sân cỏ trong hình bên, cho biết \(\widehat{AOB} = 80{^\circ}\).
Bài 6: Bánh xe (khi bơm căng) của một chiếc xe đạp có dường kính \(650\ mm\). Biết rằng khi giò đĩa quay một vòng thì bánh xe quay được khoảng \(3,3\) vòng. Hỏi chiếc xe đạp di chuyển được quãng đường dài bao nhiêu mét sau khi người đạp xe đạp \(10\) vòng liên tục?
Hướng dẫn: Khi bánh xe quay \(3,3\) vòng thì mỗi điểm trên bánh xe di chuyển được một độ dài bằng \(3,3\) lần chu vi đường tròn.
Bài 7: Cho nửa đường tròn đường kính \(AB\). Trong đoạn thẳng \(AB\) lấy hai điểm \(M\), \(N\) (\(M\) nằm giữa \(A\) và \(N\)). Vẽ các nửa đường tròn đường kính \(AM\), \(MN\), \(NB\). Chứng minh tổng của ba đường tròn đường kính \(AM\), \(MN\), \(NB\) bằng độ dài nửa đường tròn đường kính \(AB\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
---------------------------------------
Trên đây là toàn bộ kiến thức về cách tính độ dài đường tròn và độ dài cung tròn mà bạn cần biết. Hy vọng với công thức, ví dụ minh họa và cách áp dụng thực tế, bạn sẽ dễ dàng ghi nhớ và vận dụng hiệu quả trong học tập cũng như thi cử. Đừng quên lưu lại bài viết để ôn tập khi cần nhé!
