Dạng Toán tìm điều kiện trong hình học
Chuyên đề luyện thi vào lớp 10: Tìm điều kiện trong hình học
Dạng toán tìm điều kiện trong hình học là một dạng toán nâng cao có trong các đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 và giúp các bạn học sinh đạt được điểm 9, 10 trong đề thi tuyển sinh vào lớp 10. Mời các bạn tham khảo.
- Ôn thi vào lớp 10 chuyên đề 10: Chứng minh các hệ thức hình học
- Các dạng Toán thi vào 10
- Các bài toán Hình học ôn thi vào lớp 10
Tài liệu dưới đây được VnDoc biên soạn gồm hướng dẫn giải chi tiết cho dạng bài Xác định vị trí của một điểm để thỏa mãn yêu cầu đề bài để các bạn học sinh có thể luyện tập thêm. Qua đó sẽ giúp các bạn học sinh ôn tập các kiến thức, chuẩn bị cho các bài thi học kì và ôn thi vào lớp 10 hiệu quả nhất. Sau đây mời các bạn học sinh cùng tham khảo tải về bản đầy đủ chi tiết.
I. Cách giải bài toán tìm điều kiện trong hình học
1. Một số kiến thức cần nhớ
+ Tam giác là tam giác vuông khi tam giác có một góc vuông hoặc tổng hai trong ba góc bằng 900
+ Tam giác là tam giác cân khi tam giác có hai cạnh bên bằng nhau, có hai góc bằng nhau hoặc có đường trung tuyến kẻ từ một đỉnh đồng thời là đường cao, đường phân giác
+ Tam giác đều là tam giác cân có một góc bằng 600 hoặc tam giác có ba cạnh, ba góc bằng nhau
+ Tam giác vuông cân là tam giác vừa là tam giác vuông vừa là tam giác cân
+ Hình thang là tứ giác có một cặp cạnh song song với nhau
+ Một hình là hình thang cân khi hình thang có hai góc ở cùng một đáy bằng nhau, hình thang có có hai đường chéo bằng nhau hoặc hình thang có một trục đối xứng đi qua giao điểm của hai đường chéo và vuông góc với đáy
+ Hình bình hành là tứ giác có các cặp cạnh đối song song, các cặp cạnh đối bằng nhau, có hai cạnh đối song song và bằng nhau, có các góc đối bằng nhau hoặc tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường
+ Các dấu hiệu nhân biết hình thoi, hình chữ nhật và hình vuông
+ Bất đẳng thức tam giác:
Trong tam giác ABC, ta có bất đẳng thức tam giác: |AC – AB| < BC < AC + AB
2. Cách giải chung bài toán tìm điều kiện trong hình học
+ Hình A đã được cho biết trước, ta dựa vào tính chất của hình A cần tìm để tìm điều kiện của hình ban đầu hoặc các yếu tố của hình ban đầu dựa trên bài toán phân tích ngược
II. Bài tập ví dụ cho các bài tập về bài toán tìm điều kiện trong hình học
Bài 1: Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đoạn AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt tại E và F. Tiếp tuyến tại C với nửa đường tròn cắt EF tại M cắt AB tại N
a, Chứng minh M là trung điểm của EF
b, Tìm vị trí của điểm C trên đường tròn (O) sao cho tam giác CAN cân tại C
Lời giải:
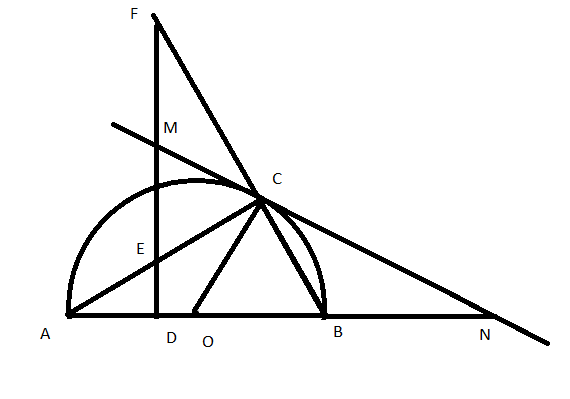
a, + Xét tam giác AED và tam giác FEC có:
![]() \(\widehat {AED} = \widehat {FEC}\)(đối đỉnh)
\(\widehat {AED} = \widehat {FEC}\)(đối đỉnh)
![]() \(\widehat {ADE} = \widehat {FCE}\left( { = {{90}^0}} \right)\)
\(\widehat {ADE} = \widehat {FCE}\left( { = {{90}^0}} \right)\)
Suy ra hai tam giác AED và tam giác FEC đồng dạng với nhau theo trường hợp góc – góc
![]() \(\Rightarrow \widehat {EAD} = \widehat {CFE}\)
\(\Rightarrow \widehat {EAD} = \widehat {CFE}\)
Lại có ![]() \(\widehat {BCN} = \widehat {CAB}\)(góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC)
\(\widehat {BCN} = \widehat {CAB}\)(góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC)
Và ![]() \(\widehat {BCN} = \widehat {FCM}\)(đối đỉnh)
\(\widehat {BCN} = \widehat {FCM}\)(đối đỉnh)
Suy ra ![]() \(\widehat {MFC} = \widehat {MCF} \Rightarrow \Delta MFC\) cân tại M, suy ra MF = MC
\(\widehat {MFC} = \widehat {MCF} \Rightarrow \Delta MFC\) cân tại M, suy ra MF = MC
+ Xét tam giác MEC vuông tại C (MC là tiếp tuyến với đường tròn) có: ME = MC
EF là cạnh huyền
Suy ra MF = MC = ME
Hay M là trung điểm của FE (đpcm)
b, + Tam giác CAN cân tại C khi và chỉ khi ![]() \(\widehat {CAN} = \widehat {CNB}\)
\(\widehat {CAN} = \widehat {CNB}\)
mà ![]() \(\widehat {CAN} = \widehat {BCN}\) (chứng minh trên)
\(\widehat {CAN} = \widehat {BCN}\) (chứng minh trên)
Suy ra ![]() \(\widehat {BCN} = \widehat {CNB}\)
\(\widehat {BCN} = \widehat {CNB}\)
Hay tam giác BCN cân tại B. Suy ra BC = BN
+ Xét tam giác OCN vuông tại có BC = BN, ON là cạnh huyền
Suy tra OB = BC = BN
Lại có OC = OB (điểm B, C thuộc đường tròn (O))
Suy ra OB = OC = BC hay tam giác OBC là tam giác đều
Vậy với điểm C nằm trên đường tròn (O) sao cho tam giác OBC đều thì tam giác CAN cân tại C
Bài 2: Cho đường tròn (O) đường kính AB = 2R. C là trung điểm của OA và dây cung MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ BM (K khác B và M). H là giao điểm của AK và MN
a, Chứng minh BCHK là tứ giác nội tiếp
b, Chứng minh AH.AK = AM2
c, Xác định vị trí của điểm K để KM + KN + KB đạt giá trị lớn nhất và tính giá trị lớn nhất đó
Lời giải:
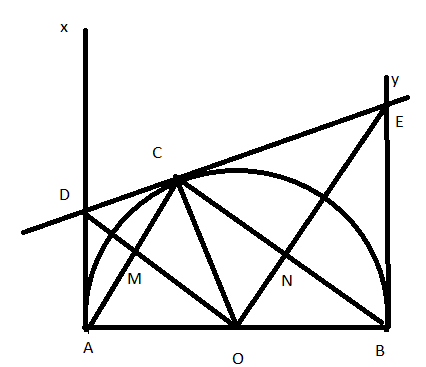
a, + Có ![]() \(\widehat {ACB}\) nhìn đường kính AB
\(\widehat {ACB}\) nhìn đường kính AB ![]() \(\Rightarrow \widehat {ACB} = {90^0}\)
\(\Rightarrow \widehat {ACB} = {90^0}\)
+ Có MN vuông góc với AB ![]() \(\Rightarrow \widehat {MCB} = {90^0}\)
\(\Rightarrow \widehat {MCB} = {90^0}\)
+ Xét tứ giác BCHK có: ![]() \(\widehat {ACB} + \widehat {BCH} = {90^0} + {90^0} = {180^0}\)
\(\widehat {ACB} + \widehat {BCH} = {90^0} + {90^0} = {180^0}\)
Hai góc ở vị trí đối nhau
Suy ra tứ giác BCHK nội tiếp đường tròn
b, + Có ![]() \(\widehat {AMB}\) nhìn đường kính AB
\(\widehat {AMB}\) nhìn đường kính AB ![]() \(\Rightarrow \widehat {AMB} = {90^0}\)
\(\Rightarrow \widehat {AMB} = {90^0}\)
+ Xét tam giác AMB: ![]() \(\widehat {AMB} = {90^0}\), MC vuông góc với AB có:
\(\widehat {AMB} = {90^0}\), MC vuông góc với AB có:
![]() \(A{M^2} = AC.AB\)(1)
\(A{M^2} = AC.AB\)(1)
+ Xét tam giác AHC và tam giác ABK có:
![]() \(\widehat {BAK}\)chung
\(\widehat {BAK}\)chung
![]() \(\widehat {ACH} = \widehat {AKB}\left( { = {{90}^0}} \right)\)
\(\widehat {ACH} = \widehat {AKB}\left( { = {{90}^0}} \right)\)
Suy ra tam giác AHC đồng dạng với tam giác ABK theo trường hợp góc - góc
![]() \(\Rightarrow \frac{{AH}}{{AB}} = \frac{{AC}}{{AK}}\)(cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow \frac{{AH}}{{AB}} = \frac{{AC}}{{AK}}\)(cặp cạnh tương ứng tỉ lệ)
![]() \(\Leftrightarrow AH.AK = AB.AC\)(2)
\(\Leftrightarrow AH.AK = AB.AC\)(2)
+ Từ (1) và (2) suy ra ![]() \(A{M^2} = AH.AK\)
\(A{M^2} = AH.AK\)
c, + Có C là trung điểm của OA ![]() \(\Rightarrow OC = \frac{{OA}}{2}\)
\(\Rightarrow OC = \frac{{OA}}{2}\)
+ Có OA = OM = ON (= R)
Suy ra ![]() \(OC = \frac{{OM}}{2} = \frac{{ON}}{2}\) và OC vuông góc với MN
\(OC = \frac{{OM}}{2} = \frac{{ON}}{2}\) và OC vuông góc với MN
![]() \(\Rightarrow \widehat {NOC} = \widehat {MOC} = {60^0} \Rightarrow \widehat {MBA} = \widehat {NBA} = {30^0} \Rightarrow \widehat {MBN} = {60^0}\)(3)
\(\Rightarrow \widehat {NOC} = \widehat {MOC} = {60^0} \Rightarrow \widehat {MBA} = \widehat {NBA} = {30^0} \Rightarrow \widehat {MBN} = {60^0}\)(3)
Ta lại có OC vuông góc với MN (4) suy ra CM = CN (5)
Từ (4) và (5) suy ra tam giác BMN cân (6)
Từ (3) và () suy ra tam giác BMN đều
+ Trên đoạn KN lấy điểm E sao cho MJ = KE (7)
Ta có ![]() \(\widehat {MKE} = \widehat {MBN} = {60^0}\), suy ra tam giác MKE đều suy ra MK = ME
\(\widehat {MKE} = \widehat {MBN} = {60^0}\), suy ra tam giác MKE đều suy ra MK = ME
+ Ta còn có MN = BM và ![]() \(\widehat {NME} = \widehat {BMK}\)(cùng hợp với
\(\widehat {NME} = \widehat {BMK}\)(cùng hợp với ![]() \(% MathType!MTEF!2!1!+-
% feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaecaaeaaca
% WGfbGaamytaiaadkeaaiaawkWaaaaa!3939!
$\widehat {EMB}\) một góc 600)
\(% MathType!MTEF!2!1!+-
% feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
% 4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9
% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x
% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaecaaeaaca
% WGfbGaamytaiaadkeaaiaawkWaaaaa!3939!
$\widehat {EMB}\) một góc 600)
Suy ra hai tam giác MNE bằng tam giác MBK theo trường hợp cạnh – góc – cạnh
Suy ra EN = KB (8)
Từ (7) và (8) suy ra KM + KN + KB = 2KN
Do đó KM + KN + KB lớn nhất khi và chỉ khi KN lớn nhất, điều đó xảy ra kbhi KN là đường kính của đường tròn tức là KN = 2R
Bài 3 BC là một dây cung của đường tròn (O; R) (BC ![]() \(\neq\) 2R). Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H.
\(\neq\) 2R). Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H.
1. Chứng minh tam giác AEF đồng dạng với tam giác ABC.
2. Gọi A’ là trung điểm của BC, Chứng minh AH = 2OA’.
3. Gọi A1 là trung điểm của EF, Chứng minh R.AA1 = AA’. OA’.
4. Chứng minh R(EF + FD + DE) = 2SABC suy ra vị trí của A để tổng EF + FD + DE đạt giá trị lớn nhất.
Lời giải: (HD)
Hình vẽ minh họa
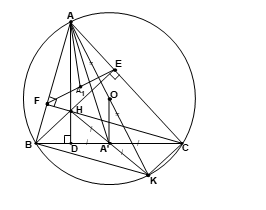
1. Tứ giác BFEC nội tiếp => ![]() \(\widehat{AEF}\ = \widehat{ACB}\) (cùng bù
\(\widehat{AEF}\ = \widehat{ACB}\) (cùng bù![]() \(\widehat{BFE}\))
\(\widehat{BFE}\))
![]() \(\ \widehat{AEF} = \widehat{ABC}\) (cùng bù
\(\ \widehat{AEF} = \widehat{ABC}\) (cùng bù![]() \(\widehat{CEF}\)) => ∆ AEF ∼ ∆ ABC.
\(\widehat{CEF}\)) => ∆ AEF ∼ ∆ ABC.
2. Vẽ đường kính AK => KB // CH ( cùng vuông góc AB); KC // BH (cùng vuông góc AC) => BHKC là hình bình hành => A’ là trung điểm của HK => OK là đường trung bình của ∆AHK => AH = 2OA’
3. Áp dụng tính chất : nếu hai tam giác đồng dạng thì tỉ số giữa hia trung tuyến, tỉ số giữa hai bán kính các đường tròn ngoại tiếp bằng tỉ số đồng dạng. ta có :
∆ AEF ∼ ∆ ABC =>  \(\frac{R}{R'}\ =
\ \frac{AA'}{AA_{1}}\) (1) trong đó R là bán kính đường tròn ngoại tiếp ∆ ABC; R’ là bán kính đường tròn ngoại tiếp ∆ AEF; AA’ là trung tuyến của ∆ ABC; AA1 là trung tuyến của ∆ AEF.
\(\frac{R}{R'}\ =
\ \frac{AA'}{AA_{1}}\) (1) trong đó R là bán kính đường tròn ngoại tiếp ∆ ABC; R’ là bán kính đường tròn ngoại tiếp ∆ AEF; AA’ là trung tuyến của ∆ ABC; AA1 là trung tuyến của ∆ AEF.
Tứ giác AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường tròn ngoại tiếp ∆ AEF
Từ (1)  \(= > \ R.AA_{1} = \ AA'.\
R' = \ AA'.\frac{AH}{2}\ = \ AA'\
.\frac{2A'O}{2}\)
\(= > \ R.AA_{1} = \ AA'.\
R' = \ AA'.\frac{AH}{2}\ = \ AA'\
.\frac{2A'O}{2}\)
Vậy R . AA1 = AA’ . A’O (2)
4. Gọi B’, C’lần lượt là trung điểm của AC, AB, ta có OB’⊥ AC ; OC’⊥ AB (bán kính đi qua trung điểm của một dây không qua tâm) => OA’, OB’, OC’ lần lượt là các đường cao của các tam giác OBC, OCA, OAB.
SABC = SOBC+ SOCA + SOAB =![]() \(\frac{1}{2}\)( OA’ . BC’ + OB’ . AC + OC’ . AB )
\(\frac{1}{2}\)( OA’ . BC’ + OB’ . AC + OC’ . AB )
2SABC = OA’ . BC + OB’ . AC’ + OC’ . AB (3)
Theo (2) => OA’ = R .  \(\frac{AA_{1}}{AA'}\) mà
\(\frac{AA_{1}}{AA'}\) mà  \(\frac{AA_{1}}{AA'}\)là tỉ số giữa 2 trung tuyến của hai tam giác đồng dạng AEF và ABC nên
\(\frac{AA_{1}}{AA'}\)là tỉ số giữa 2 trung tuyến của hai tam giác đồng dạng AEF và ABC nên  \(\frac{AA_{1}}{AA'}\) =
\(\frac{AA_{1}}{AA'}\) = ![]() \(\frac{EF}{BC}\).
\(\frac{EF}{BC}\).
Tương tự ta có : OB’ = R .![]() \(\frac{FD}{AC}\); OC’ = R .
\(\frac{FD}{AC}\); OC’ = R . ![]() \(\frac{ED}{AB}\) Thay vào (3) ta được
\(\frac{ED}{AB}\) Thay vào (3) ta được
2SABC = R (![]() \(\frac{EF}{BC}.BC +
\frac{FD}{AC}.AC + \frac{ED}{AB}.AB\)) 2SABC = R(EF + FD + DE)
\(\frac{EF}{BC}.BC +
\frac{FD}{AC}.AC + \frac{ED}{AB}.AB\)) 2SABC = R(EF + FD + DE)
* R(EF + FD + DE) = 2SABC mà R không đổi nên (EF + FD + DE) đạt gí trị lớn nhất khi SABC.
Ta có SABC = ![]() \(\frac{1}{2}\)AD.BC do BC không đổi nên SABC lớn nhất khi AD lớn nhất, mà AD lớn nhất khi A là điểm chính giữa của cung lớn BC.
\(\frac{1}{2}\)AD.BC do BC không đổi nên SABC lớn nhất khi AD lớn nhất, mà AD lớn nhất khi A là điểm chính giữa của cung lớn BC.
Bài 4 Cho đường tròn (O) đường kính AB. Gọi I là trung điểm của OA . Vẽ đường tròn tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q.
1. Chứng minh rằng các đường tròn (I) và (O) tiếp xúc nhau tại A.
2. Chứng minh IP // OQ.
3. Chứng minh rằng AP = PQ.
4. Xác định vị trí của P để tam giác AQB có diện tích lớn nhất.
Lời giải:
Hình vẽ minh họa
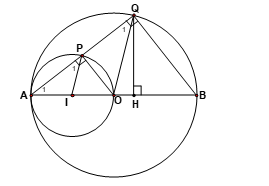
1. Ta có OI = OA – IA mà OA và IA lần lượt là các bán kính của đ/ tròn (O) và đường tròn (I) . Vậy đ/ tròn (O) và đường tròn (I) tiếp xúc nhau tại A .
2. ∆ OAQ cân tại O ( vì OA và OQ cùng là bán kính ) => ![]() \(\widehat{A_{1}} = \widehat{Q_{1}}\)
\(\widehat{A_{1}} = \widehat{Q_{1}}\)
∆ IAP cân tại I ( vì IA và IP cùng là bán kính ) => ![]() \(\widehat{A_{1}} = \widehat{P_{1}}\)
\(\widehat{A_{1}} = \widehat{P_{1}}\)
![]() \(= > \widehat{P_{1}} =
\widehat{Q_{1}}\) mà đây là hai góc đồng vị nên suy ra IP // OQ.
\(= > \widehat{P_{1}} =
\widehat{Q_{1}}\) mà đây là hai góc đồng vị nên suy ra IP // OQ.
3. ![]() \(\widehat{APO}\ = \ 90^{0}\) (nội tiếp chắn nửa đường tròn ) => OP ⊥ AQ => OP là đường cao của ∆OAQ mà ∆OAQ cân tại O nên OP là đường trung tuyến => AP = PQ.
\(\widehat{APO}\ = \ 90^{0}\) (nội tiếp chắn nửa đường tròn ) => OP ⊥ AQ => OP là đường cao của ∆OAQ mà ∆OAQ cân tại O nên OP là đường trung tuyến => AP = PQ.
4. (HD) Kẻ QH ⊥ AB ta có SAQB = ![]() \(\frac{1}{2}\)AB.QH. mà AB là đường kính không đổi nên SAQB lớn nhất khi QH lớn nhất. QH lớn nhất khi Q trùng với trung điểm của cung AB. Để Q trùng với trung điểm của cung AB thì P phải là trung điểm của cung AO.
\(\frac{1}{2}\)AB.QH. mà AB là đường kính không đổi nên SAQB lớn nhất khi QH lớn nhất. QH lớn nhất khi Q trùng với trung điểm của cung AB. Để Q trùng với trung điểm của cung AB thì P phải là trung điểm của cung AO.
Thật vậy P là trung điểm của cung AO => PI ⊥ AO mà theo trên PI // QO => QO ⊥ AB tại O => Q là trung điểm của cung AB và khi đó H trung với O; OQ lớn nhất nên QH lớn nhất.
III. Bài tập tự luyện các bài toán về tìm điều kiện trong hình học
Bài 1: Từ một điểm A bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn. Gọi M là trung điểm của AB. Tia CM cắt đường tròn tại điểm N. Tia AN cắt đường tròn tại điểm D
a, Chứng minh rằng MB2 = MC.MN
b, Chứng minh rằng AB // CD
c, Tìm điều kiện của điểm A để cho tứ giác ABDC là hình thoi. Tính diện tích của hình thoi đó
Bài 2: Cho đường tròn (O; R), đường kính AB, dây cung MN khác đường kính vuông góc với AB tại I (điểm I sao cho IA < IB). Trên đoạn MI lấy điểm E (E khác M và E khác I). Tia AE cắt đường tròn tại điểm thứ hai là K. Chứng minh:
a, IEKB nội tiếp đường tròn
b, AE. AK + BI.BA = R2
c, Giả sử I là trung điểm của OA. Xác định vị trí của K để KM + KN + KB đạt giá trị lớn nhất
Bài 3: Cho AB và CD là hai đường kính vuông góc với nhau của đường tròn (O; R). Qua điểm M thuộc cung nhỏ AC (M khác A và E), kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E, F
a, Chứng minh ![]() \(\widehat {MFO} = 2\widehat {MBO}\)
\(\widehat {MFO} = 2\widehat {MBO}\)
b, Xác định vị trí điểm M trên cung nhỏ AC sao cho . Khi đó tính độ dài đoạn thẳng OE, ME, EF theo R.
Bài 4: Cho tam giác ABC (AB > AC) nội tiếp nửa đường tròn đường kính AB. Gọi H là chân đường vuông góc kẻ từ A đến tiếp tuyến với đường tròn tại C. AH cắt đường tròn tại M. Đường vuông góc với AC kẻ từ M cắt AC tại K và AB tại P
a) Chứng minh tứ giác MKCH nội tiếp
b) AC là phân giác của MAB
c) Tìm điều kiện tam giác ABC để M, K, O thẳng hàng
Bài 5: Cho đường tròn (O;R) có đường kính AB cố định. Vẽ đường kính MN của đường tròn (O) (M khác A, M khác B). Tiếp tuyến của đường tròn (O) tại B cắt các đường thẳng AM, AN lần lượt tại các điểm Q, P.
1) Chứng minh tứ giác AMBN là hình chữ nhật.
2) Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn.
3) Gọi E là trung điểm của BQ. Đường thẳng vuông góc với OE tại O cắt PQ tại điểm F. Chứng minh F là trung điểm của BP và ME // NF.
4) Khi đường kính MN quay quanh tâm O và thỏa mãn điều kiện đề bài, xác định vị trí của đường kính MN để tứ giác MNPQ có diện tích nhỏ nhất.
-------------------
Ngoài các dạng Toán 9 ôn thi vào lớp 10 trên, mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt!









