VnDoc.com

Hình cầu. Công thức tính hình cầu

Chuyên đề Toán 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Công thức hình cầu

A. Công thức hình cầu
- Diện tích mặt cầu
- Thể tích hình cầu
B. Bài tập tính hình cầu
C. Bài tập từ rèn luyện

Hình cầu là một hình khối tròn xoay đặc biệt, thường gặp trong các bài toán hình học không gian lớp 9 và THPT. Để giải nhanh và chính xác các bài toán liên quan, học sinh cần nắm chắc các công thức tính diện tích mặt cầu và thể tích hình cầu. Bài viết này sẽ cung cấp đầy đủ lý thuyết, công thức trọng tâm và ví dụ minh họa giúp bạn học tốt và ứng dụng hiệu quả trong quá trình làm bài.

A. Công thức hình cầu

Hình vẽ minh họa

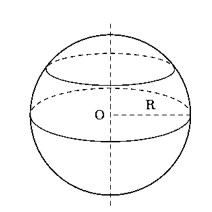
Diện tích mặt cầu

$S = 4\pi R^{2}$ $S = 4 π R^{2}$ hay $S = \pi d^{2}$ $S = π d^{2}$ .

Với $R$ là bán kính và d là đường kính của mặt cầu.

Thể tích hình cầu

$V = \frac{4}{3}\pi R^{3}$ $V = \frac{4}{3} π R^{3}$

B. Bài tập tính hình cầu

Dạng 1: Tính diện tích mặt cầu, thể tích hình cầu và các đại lượng liên quan

Phương pháp:

Áp dụng công thức tính diện tích mặt cầu, thể tích hình cầu để giải bài toán

Bài 1. Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai, đơn vị: mm):

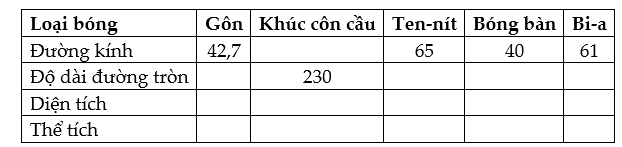
Hướng dẫn giải

Áp dụng công thức ta có kết quả ghi lại như sau:

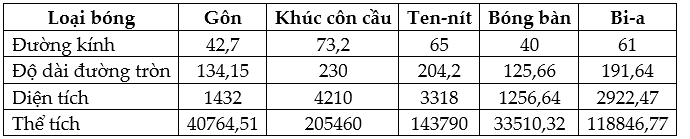
Bài 2. Diện tích của một mặt cầu là $2464$ m² thì đường kính của mặt cầu là bao nhiêu? (Lấy $\pi = \frac{22}{7}$ $π = \frac{22}{7}$ ).

A. $28$ cm. B. $28$ mét. C. $38$ mét. D. $30$ mét.

Hướng dẫn giải

Áp dụng công thức tính diện tích mặt cầu và biến đổi ta được

$S = \pi d^{2} = 2464 \Rightarrow d = \sqrt{\frac{2464}{\pi}} \Rightarrow d = \sqrt{\frac{2464}{\frac{22}{7}}} = 28$ $S = π d^{2} = 2464 \Rightarrow d = \sqrt{\frac{2464}{π}} \Rightarrow d = \sqrt{\frac{2464}{\frac{22}{7}}} = 28$ mét.

(Đơn vị của diện tích mặt cầu là m $\ ^{2}$ $^{2}$ ).

Bài 3. Thể tích của một hình cầu là $\frac{4312}{3}$ $\frac{4312}{3}$ cm². Thì bán kính của hình cầu là bao nhiêu? (Lấy $\pi =\frac{22}{7}$ $π = \frac{22}{7}$ ).

A. $7$ cm. B. $8$ cm. C. $9$ cm. D. $10$ cm.

Hướng dẫn giải

Áp dụng công thức tính thể tích hình cầu và biến đổi ta được

$V = \frac{4}{3}\pi R^{3} = \frac{4312}{3}. \Rightarrow R = \sqrt[3]{\frac{4312 \cdot 3}{3 \cdot 4\pi}} \Rightarrow R = \sqrt[3]{\frac{4312}{4 \cdot \frac{22}{7}}} = 7$ $V = \frac{4}{3} π R^{3} = \frac{4312}{3} . \Rightarrow R = \sqrt[3]{\frac{4312 \cdot 3}{3 \cdot 4 π}} \Rightarrow R = \sqrt[3]{\frac{4312}{4 \cdot \frac{22}{7}}} = 7$ cm.

Dạng 2: Dạng toán tổng hợp

Phương pháp:

Vận dụng linh hoạt các kiến thức đã được học kết hợp với các công thức và lý thuyết về hình cầu để giải bài tập.

Bài 1. Một hình nón có bán kính đáy bằng $3$ cm và có diện tích xung quanh bằng diện tích của mặt cầu có bán kính $3$ cm. Tính chiều cao của hình nón.

Hướng dẫn giải

Áp dụng công thức tính diện tích xung quanh hình nón $S_{xq} = \pi rl = 3\pi l$ $S_{x q} = π r l = 3 π l$ .

Áp dụng công thức tính diện tích mặt cầu $S_{c} = 4\pi R^{2} = 36\pi$ $S_{c} = 4 π R^{2} = 36 π$ .

Từ giả thuyết $S_{xq} = S_{c}$ $S_{x q} = S_{c}$ ta được $3\pi l = 36\pi$ $3 π l = 36 π$ $\Rightarrow l = 12 \Rightarrow h = \sqrt{12^{2} - 3^{2}} = 3\sqrt{15}$ $\Rightarrow l = 12 \Rightarrow h = \sqrt{12^{2} - 3^{2}} = 3 \sqrt{15}$ cm.

Bài 2: Cho đường tròn $(O; R)$ ngoại tiếp tam giác đều $A B C$ . Quay đường tròn này một vòng quanh đường kính $A O D$ ta được một hình cầu ngoại tiếp một hình nón. Tính thể tích phần bên trong hình cầu và bên ngoài hình nón?

Hướng dẫn giải

Hình vẽ minh họa

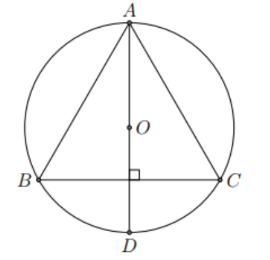
Độ dài cạnh của tam giác đều là: $AB = R\sqrt{3}$ $A B = R \sqrt{3}$

Bán kính đáy hình tròn là: $r = \frac{R\sqrt{3}}{2}$ $r = \frac{R \sqrt{3}}{2}$ .

Chiều cao hình nón là: $h = \frac{R\sqrt{3}.\sqrt{3}}{2} = \frac{3R}{2}$ $h = \frac{R \sqrt{3} . \sqrt{3}}{2} = \frac{3 R}{2}$

Thể tích hình cầu là: $V_{1} = \frac{4}{3}\pi r^{3}$ $V_{1} = \frac{4}{3} π r^{3}$

Thể tích hình nón là: $V_{2} = \frac{1}{3}\pi r^{2}h = \frac{1}{3}\pi\left( \frac{R\sqrt{3}}{2} \right)^{2}.\frac{3}{2}R = \frac{3}{8}\pi R^{3}$ $V_{2} = \frac{1}{3} π r^{2} h = \frac{1}{3} π {(\frac{R \sqrt{3}}{2})}^{2} . \frac{3}{2} R = \frac{3}{8} π R^{3}$

Thể tích phần cần tìm là: $V = V_{1} - V_{2} = \frac{23}{24}.\pi R^{3}$ $V = V_{1} - V_{2} = \frac{23}{24} . π R^{3}$

Bài 3: Một hình nón có đỉnh là tâm một hình cầu và có đáy là hình tròn tạo bởi một mặt phẳng cắt hình cầu. Biết diện tích đáy hình nón là $144\pi{cm}^{2}$ $144 π {c m}^{2}$ và diện tích xung quanh của nó là $180\pi{cm}^{2}$ $180 π {c m}^{2}$ . Tính thể tích phần không gian bên trong hình cầu và bên ngoài hình nón.

Hướng dẫn giải

Hình vẽ minh họa

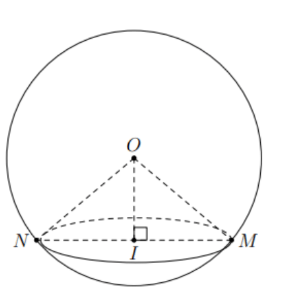
Tính bán kính đáy hình nón là

$\pi \cdot IM^{2} \cdot 144\pi \Leftrightarrow r = IM = 12\text{\ }cm$ $π \cdot I M^{2} \cdot 144 π \Leftrightarrow r = I M = 12 \ c m$

Tính đường sinh hình nón là

$S_{xq} = 180\pi \Leftrightarrow \pi \cdot r \cdot l = 180\pi \Leftrightarrow l = OM = 15cm$ $S_{x q} = 180 π \Leftrightarrow π \cdot r \cdot l = 180 π \Leftrightarrow l = O M = 15 c m$

Chiều cao hình nón là

$h = OI = \sqrt{OM^{2} - IM^{2}} = \sqrt{l^{2} - r^{2}} = 9cm$ $h = O I = \sqrt{O M^{2} - I M^{2}} = \sqrt{l^{2} - r^{2}} = 9 c m$

Tính hiệu thể tích giữa hình cầu và hình nón được

$V = V_{\text{cau~}} - V_{\text{nón~}} = \frac{4}{3}\pi \cdot OM^{3} - \frac{1}{3}\pi \cdot IM^{2} \cdot h = 4068\pi{cm}^{3}$ $V = V_{cau~} - V_{nón~} = \frac{4}{3} π \cdot O M^{3} - \frac{1}{3} π \cdot I M^{2} \cdot h = 4068 π {c m}^{3}$

C. Bài tập từ rèn luyện

Bài 1. Một cái hộp hình trụ được làm ra sao cho một quả bóng hình cầu đặt vừa khít vào hộp đó như hình vẽ. Tỉ số thể tích của hình cầu và hình trụ là

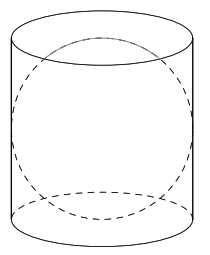
A. $\frac{3}{4}$ $\frac{3}{4}$ . B. $\frac{4}{3}$ $\frac{4}{3}$ . C. $\frac{3}{2}$ $\frac{3}{2}$ . D. $\frac{2}{3}$ $\frac{2}{3}$ .

Bài 2. Chiều cao của một hình trụ gấp 3 lần bán kính đáy của nó. Tỉ số của thể tích hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là

A. $\frac{4}{3}$ $\frac{4}{3}$ . B. $\frac{9}{4}$ $\frac{9}{4}$ . C. $\frac{3}{1}$ $\frac{3}{1}$ . D. $\frac{4}{9}$ $\frac{4}{9}$ .

Bài 3. Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính $r = 12$ cm như hình vẽ.

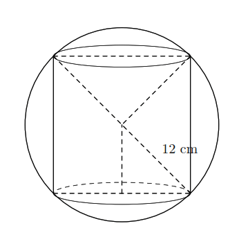
Tính:

a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.

b) Thể tích của hình cầu.

c) Diện tích mặt cầu.

Bài 4. Cho tam giác đều $A B C$ có cạnh $A B = 8$ cm, đường cao $A H$ . Khi đó diện tích mặt cầu được tạo thành khi quay nửa đường tròn nội tiếp $\bigtriangleup ABC$ $△ A B C$ một vòng quanh $A H$ .

------------------------------------------------

Với những kiến thức đã trình bày, bạn chắc chắn đã hiểu rõ về đặc điểm và công thức tính diện tích, thể tích hình cầu. Việc ghi nhớ và vận dụng đúng sẽ giúp bạn tự tin khi gặp dạng toán hình học không gian này trong các bài kiểm tra và kỳ thi. Đừng quên luyện tập thêm nhiều dạng bài khác để củng cố và mở rộng kiến thức nhé!

Chia sẻ, đánh giá bài viết

1

24

Bài trước

Bài sau

Chia sẻ bởi:
Bọ Cạp

Tải về

Chọn file muốn tải về:

Hình cầu. Công thức tính hình cầu

531,5 KB

File Word

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!