VnDoc.com

Hình nón. Công thức hình nón

Chuyên đề Toán 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Công thức tính hình nón

A. Công thức hình nón
B. Bài tập tính hình nón

Hình nón là một hình khối quen thuộc trong hình học không gian, thường xuất hiện trong chương trình Toán THCS và THPT. Việc nắm vững các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích hình nón sẽ giúp bạn giải nhanh các bài toán liên quan. Bài viết này sẽ tổng hợp đầy đủ kiến thức lý thuyết, công thức và ví dụ minh họa về hình nón một cách dễ hiểu và chính xác.

A. Công thức hình nón

Hình vẽ minh họa

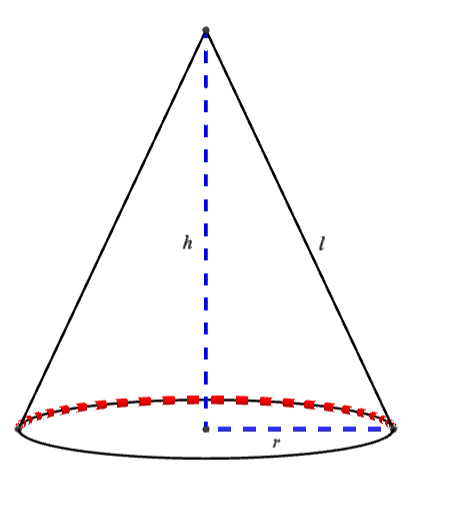
Diện tích xung quanh hình nón

$S_{xq} = \pi.r.l$ $S_{x q} = π . r . l$

Sxq: là diện tích xung quanh hình nón
π: là hằng số Pi = 3,14
r: Bán kính vòng tròn đấy hình nón
l: đường sinh của hình nón

- Diện tích xung quanh hình nón bằng một nửa tích của chu vi đường tròn đáy và độ dài đường sinh.

Diện tích toàn phần hình nón

$S_{tp} = S_{xq} + S_{d} = \pi rl + \pi r^{2}$ $S_{t p} = S_{x q} + S_{d} = π r l + π r^{2}$

Stp: là diện tích toàn phần hình nón
π: là hằng số Pi = 3,14
r: Bán kính vòng tròn
l: đường sinh

- Diện tích toàn phần hình nón bằng diện tích xung quanh cộng với diện tích đáy.

Thể tích hình nón

$V = \frac{1}{3}\pi r^{2}h$ $V = \frac{1}{3} π r^{2} h$

V: là thể tích hình nón
π: là hằng số Pi = 3,14
r: Bán kính vòng tròn
h: là đường cao hạ từ đỉnh xuống đấy hình nón

- Thể tích hình nón bằng một phần ba diện tích đáy nhân với chiều cao.

B. Bài tập tính hình nón

Bài 1. Cho $\Delta ABC$ $Δ A B C$ vuông tại A, có AB = 3 cm, AC = 4cm.

a) Tính chiều cao AH của $\Delta ABC$ $Δ A B C$ .

b) Cho $\Delta ABC$ $Δ A B C$ quay một vòng quanh cạnh BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra.

Hướng dẫn giải

a) Ta có:

$BC = \sqrt{3^{2} + 4^{2}} = 5(cm)$ $B C = \sqrt{3^{2} + 4^{2}} = 5 (c m)$

$\Rightarrow AH = \frac{3.4}{5} = 2,4(cm)$ $\Rightarrow A H = \frac{3.4}{5} = 2, 4 (c m)$

b) Diện tích hình nón do phần dây cung AB tạo ra nhận AB là đường sinh, AH là bán kính đáy: $S_{1} = \pi.AH.AB$ $S_{1} = π . A H . A B$

Diện tích hình nón do phần dây cung AC tạo ra nhận AC là đường sinh, AH là bán kính đáy: $S_{2} = \pi.AH.AC$ $S_{2} = π . A H . A C$

$\Rightarrow \frac{S_{1}}{S_{2}} = \frac{\pi.AH.AB}{\pi.AH.AC} = \frac{3}{4}$ $\Rightarrow \frac{S_{1}}{S_{2}} = \frac{π . A H . A B}{π . A H . A C} = \frac{3}{4}$

Bài 2. Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Cho biết BC = 4 dm, $\widehat{ACB} = 30^{0}$ $\hat{A C B} = 30^{0}$ . Tính diện tích xung quanh và thể tích của hình nón.

Hướng dẫn giải

Hình vẽ minh họa

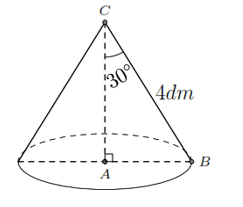
$AB = 4sin30^{0} = 2$ $A B = 4 s i n 30^{0} = 2$ dm, $AC = 4cos30^{0} = 2\sqrt{3}$ $A C = 4 c o s 30^{0} = 2 \sqrt{3}$ dm

$\Rightarrow S_{xq} = \pi.2.4 = 8\pi$ $\Rightarrow S_{x q} = π .2 .4 = 8 π$ dm².

Áp dụng công thức tính thể tích hình chóp nón $V = \frac{1}{3}\pi.2^{2}.2\sqrt{3} = \frac{8\sqrt{3}\pi}{3}$ $V = \frac{1}{3} π {.2}^{2} .2 \sqrt{3} = \frac{8 \sqrt{3} π}{3}$ dm³

Bài 3. Cho hình nón cụt có hai bán kính 9 cm, 14cm. Chiều cao của hình nón là 12 cm. Tính diện tích xung quanh và thể tích của hình nón cụt.

Hướng dẫn giải

Từ giả thuyết ta tính được $l = \sqrt{12^{2} + 5^{2}} = 13$ $l = \sqrt{12^{2} + 5^{2}} = 13$ cm.

Áp dụng công thức tính diện tích xung quanh hình nón cụt:

$S_{tp} = \pi(14 + 9).13 = 299\pi\left( cm^{2} \right)$ $S_{t p} = π (14 + 9) .13 = 299 π (c m^{2})$

Áp dụng công thức tính thể tích hình nón cụt:

$V = \frac{1}{3}\pi h\left( {r_{1}}^{2} + {r_{2}}^{2} + r_{1}.r_{2} \right) = 1612\pi\left( cm^{3} \right)$ $V = \frac{1}{3} π h ({r_{1}}^{2} + {r_{2}}^{2} + r_{1} . r_{2}) = 1612 π (c m^{3})$

Bài 4. Tính thể tích của các hình bên dưới theo các kích thước đã cho.

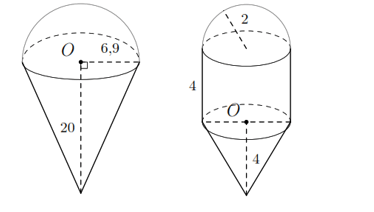
Hướng dẫn giải

Kết hợp công thức tính thể tích hình cầu $V = \frac{4}{3}\pi R^{3}$ $V = \frac{4}{3} π R^{3}$ và thể tích hình trụ $V = \pi r^{2}h$ $V = π r^{2} h$ ta được:

$V = \pi \cdot \left( \frac{12,6}{2} \right)^{2} \cdot 8,4 + \frac{1}{2} \cdot \frac{4}{3}\pi \cdot \left( \frac{12,6}{2} \right)^{3} = 500,094\pi$ $V = π \cdot {(\frac{12, 6}{2})}^{2} \cdot 8, 4 + \frac{1}{2} \cdot \frac{4}{3} π \cdot {(\frac{12, 6}{2})}^{3} = 500, 094 π$

Kết hợp công thức tính thể tích hình cầu $V = \frac{4}{3}\pi R^{3}$ $V = \frac{4}{3} π R^{3}$ và thể tích hình chóp nón $V = \frac{1}{3}\pi r^{2}h$ $V = \frac{1}{3} π r^{2} h$ tađược:

$V = \frac{1}{3}\pi \cdot 6,9^{2} \cdot 20 + \frac{1}{2} \cdot \frac{4}{3}\pi \cdot 6,9^{3} = 536,406\pi$ $V = \frac{1}{3} π \cdot 6, 9^{2} \cdot 20 + \frac{1}{2} \cdot \frac{4}{3} π \cdot 6, 9^{3} = 536, 406 π$

Kết hợp công thức tính thể tích hình cầu $V = \frac{4}{3}\pi R^{3}$ $V = \frac{4}{3} π R^{3}$ , thể tích hình trụ $V = \pi r^{2}h$ $V = π r^{2} h$ và thể tích hình chóp nón $V = \frac{1}{3}\pi r^{2}h$ $V = \frac{1}{3} π r^{2} h$ ta được:

$V = \frac{1}{3}\pi \cdot 2^{2} \cdot 4 + \pi \cdot 2^{2} \cdot 4 + \frac{1}{2} \cdot \frac{4}{3}\pi \cdot 2^{3} = \frac{80\pi}{3}$ $V = \frac{1}{3} π \cdot 2^{2} \cdot 4 + π \cdot 2^{2} \cdot 4 + \frac{1}{2} \cdot \frac{4}{3} π \cdot 2^{3} = \frac{80 π}{3}$

--------------------------------------------

Qua bài viết, bạn đã được trang bị đầy đủ kiến thức về hình nón và các công thức quan trọng liên quan. Hãy áp dụng linh hoạt vào các bài tập thực tế để hiểu sâu hơn và nâng cao kỹ năng giải toán không gian. Đừng quên luyện tập thường xuyên và tham khảo thêm các chuyên đề hình học khác để học tốt hơn mỗi ngày!

Chia sẻ, đánh giá bài viết

1

92

Bài trước

Bài sau

Chia sẻ bởi:
Đen2017

Tải về

Chọn file muốn tải về:

Hình nón. Công thức hình nón

216,9 KB

File Word

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!