Cho hàm số . Xét tính đúng sai của nhận định dưới đây:
a) Đạo hàm của hàm số đã cho là . Đúng||Sai
b) Hàm số đã cho đồng biến trên khoảng và nghịch biến trên các khoảng
. Sai||Đúng
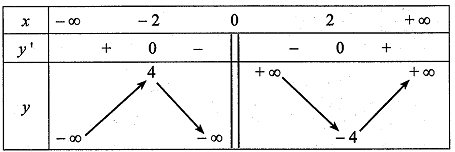
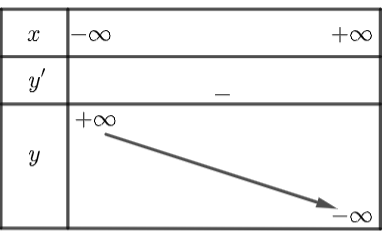
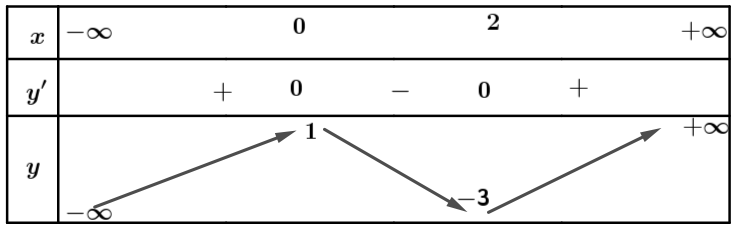
c) Bảng biến thiên của hàm số đã cho là:
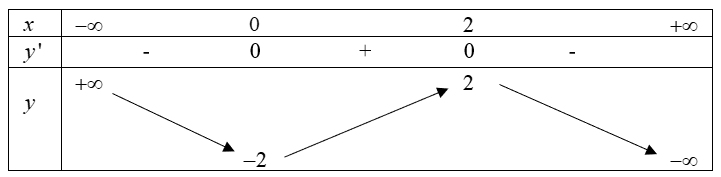
Sai||Đúng
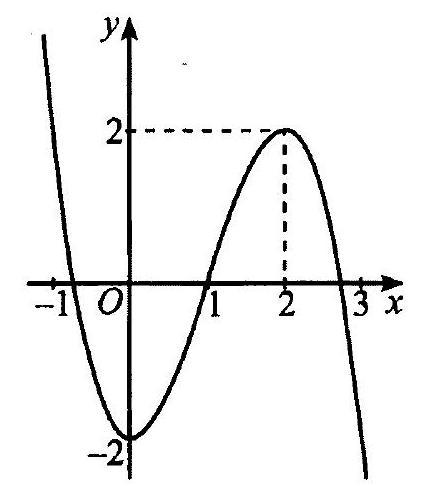
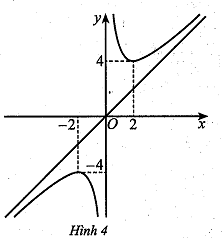
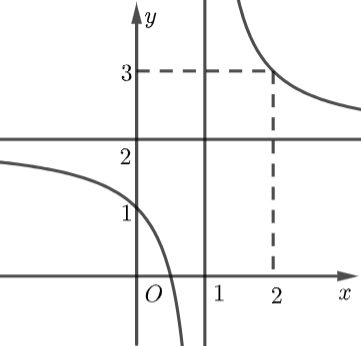
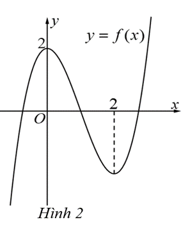
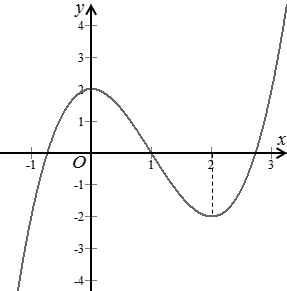
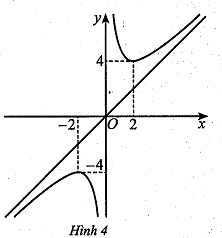
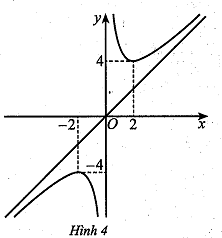
d) Đồ thị hàm số đã cho như ở Hình 4.
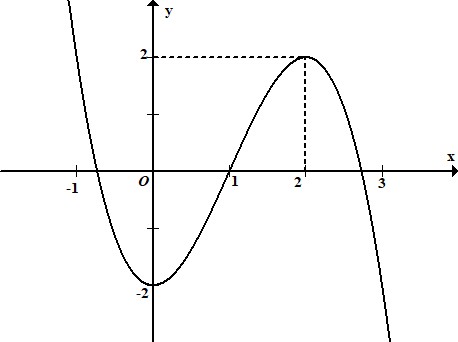
Sai||Đúng
Cho hàm số . Xét tính đúng sai của nhận định dưới đây:
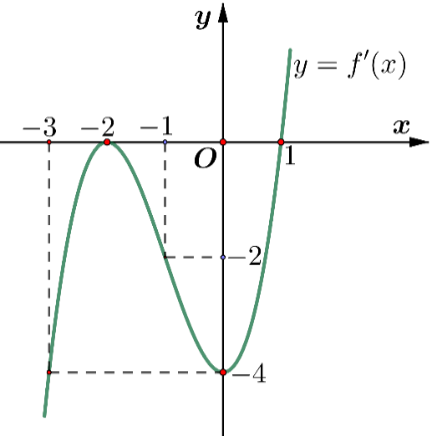
a) Đạo hàm của hàm số đã cho là . Đúng||Sai
b) Hàm số đã cho đồng biến trên khoảng và nghịch biến trên các khoảng
. Sai||Đúng
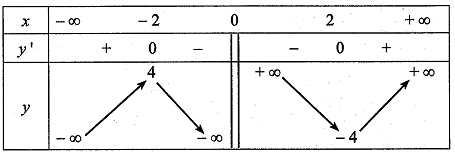
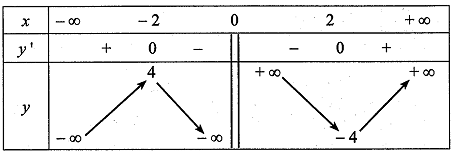
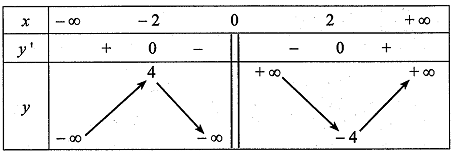
c) Bảng biến thiên của hàm số đã cho là:

Sai||Đúng
d) Đồ thị hàm số đã cho như ở Hình 4.

Sai||Đúng
|
Câu 2 |
a) |
b) |
c) |
d) |
|
ý |
Đúng |
Sai |
Sai |
Sai |
Ta có: ,
hoặc
.
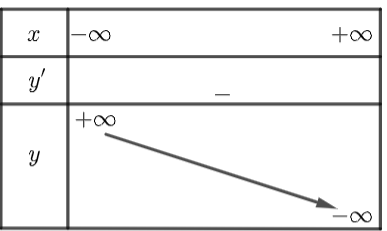
Bảng biến thiên của hàm số đã cho là:
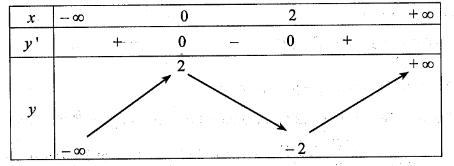
Hàm số đồng biến trên các khoảng và
, hàm số nghịch biến trên khoảng
.
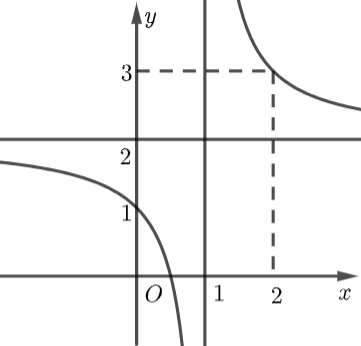
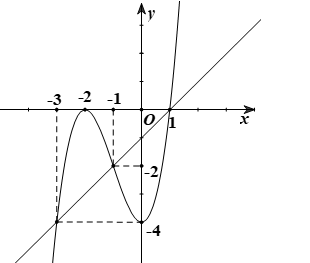
Đồ thị hàm số đã cho là:
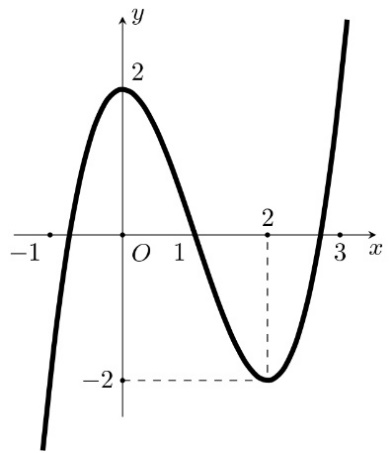
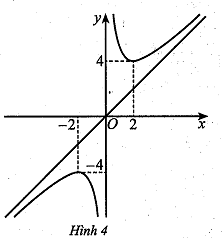 .
.
 .
.
 .
.












 .
.