VnDoc.com

Bài toán quy hoạch tuyến tính hai biến

Ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại: Tài liệu Lẻ

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách giải bài toán quy hoạch tuyến tính hai biến Toán 12

Bài toán quy hoạch tuyến tính hai biến là dạng toán vận dụng – vận dụng cao thường gặp trong chương trình Toán 12, gắn với các bài toán thực tế và xuất hiện trong đề thi THPT Quốc gia môn Toán những năm gần đây.

Bài viết giúp học sinh nắm chắc cách xác định miền nghiệm, điểm tối ưu và giá trị lớn nhất – nhỏ nhất, từ đó giải nhanh và chính xác các bài toán quy hoạch tuyến tính hai biến Toán 12.

A. Bài toán Quy hoạch tuyến tính hai biến

Tìm giá trị lớn nhất (tương ứng, giá trị nhỏ nhất) của biểu thức trên miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

$S:\left\{ \begin{matrix} a_{1}x + b_{1}y \leq c_{1} \\ a_{2}x + b_{2}y \leq c_{2} \\ ... \\ a_{n}x + b_{n}y \leq c_{n} \end{matrix} \right.\ \ \ \ \ (1)$

Ở đó là các số thực cho trước, không đồng thời bằng .

Các bài toán như này được gọi là bài toán quy hoạch tuyến tính hai biến. Biểu thức ở trên được gọi là hàm mục tiêu.

Chú ý:

a) Mỗi bất phương trình trong hệ (1) gọi là một ràng buộc. Nếu $\left( x_{0};y_{0} \right)$ là một nghiệm của hệ bất phương trình (1) thì ta nói $\left( x_{0};y_{0} \right)$ là phương án chấp nhận được hoặc phương án khả thi của bài toán. Tập các phương án chấp nhận được còn được gọi là miền chấp nhận được. Nếu đạt giá trị lớn nhất (tương ứng, giá trị nhỏ nhất) trên miền nghiệm tại $\left( x_{0};y_{0} \right)$ thì cặp $\left( x_{0};y_{0} \right)$ gọi là phương án tối ưu của bai toán và giá trị $F\left( x_{0};y_{0} \right)$ gọi là giá trị tối ưu.

b) Bài toán quy hoạch tuyến tính trên được kí hiệu như sau:

$F(x;y) = Ax + By \rightarrow \max\left( \min \right)$ với các ràng buộc $\left\{ \begin{matrix} a_{1}x + b_{1}y \leq c_{1} \\ a_{2}x + b_{2}y \leq c_{2} \\ ... \\ a_{n}x + b_{n}y \leq c_{n} \end{matrix} \right.$ .

c) Trong hệ (1) một số ràng buộc có thể được viết dưới dạng $ax + by \geq c$ .

Ví dụ: Một cơ sở sản xuất dự định sản xuất hai loại sản phẩm và . Các sản phẩm được chế tạo từ ba loại nguyên liệu . Số lượng dự trữ của từng loại và số lượng từng loại nguyên liệu cần dùng để sản xuất ra một sản phẩm được cho bằng bảng sau:

Loại nguyên liệu	Nguyên liệu dự trữ	Nguyên liệu cần dùng để sản xuất một đơn vị sản phẩm
Loại nguyên liệu	Nguyên liệu dự trữ	A	B
I	18	2	3
II	30	5	4
III	25	1	6

Hãy lập quy hoạch sản xuất để thu được tiền lãi lớn nhất, biết rằng tiền lãi thu được khi bán một sản phẩm A là 3 triệu đồng, một sản phẩm B là 2 triệu đồng.

Hướng dẫn

Gọi lần lượt là số sản phẩm A, B cần sản xuất theo kế hoạch.

Khi đó, tiền lãi thu được là:

(triệu đồng)

Những ràng buộc thuộc về nguyên liệu dự trữ là:

$2x + 3y \leq 18$ (ràng buộc về nguyên liệu I)

$5x + 4y \leq 30$ (ràng buộc về nguyên liệu II)

$x + 6y \leq 25$ (ràng buộc về nguyên liệu III)

Ngoài ra, còn các ràng buộc tự nhiên là: $x;y \geq 0$ . Vì số đơn vị sản phẩm không thể âm. Như vậy bài toán có thể phát biểu như sau:

Tìm sao cho tại đó biểu thức đạt giá trị lớn nhất, với các ràng buộc: $\left\{ \begin{matrix} 2x + 3y \leq 18 \\ 5x + 4y \leq 30 \\ x + 6y \leq 25 \\ x \geq 0;y \geq 0 \end{matrix} \right.\ \ \ \ (*)$

B. Bài tập minh họa bài toán quy hoạch tuyến tính hai biến

Bài tập 1: Một xưởng sản xuất đồ gỗ mỹ nghệ sản suất ra hai loại sản phẩm I và II. Mỗi bộ sản phẩm loại I lãi 5 triệu đồng, mỗi bộ sản phẩm loại II lãi 4 triệu đồng. Để sản suất mỗi bộ sản phẩm loại I cần máy làm việc trong 3 giờ và nhân công làm việc trong 2 giờ. Để sản suất mỗi bộ sản phẩm loại II cần máy làm việc trong 3 giờ và nhân công làm việc trong 1 giờ. Biết rằng chỉ dùng máy hoặc chỉ dùng nhân công, không thể đồng thời làm hai loại sản phẩm cùng lúc, số nhân công luôn ổn định. Một ngày máy làm việc không quá 15 giờ, nhân công làm việc không quá 8 giờ. Hỏi một ngày tiền lãi lớn nhất bằng bao nhiêu?

Hướng dẫn giải

Gọi số bộ sản phẩm loại I sản xuất trong một ngày là: $x\ (x \geq 0)$ .

Số bộ sản phẩm loại II sản xuất trong một ngày là: $y\ (y \geq 0)$ .

Số lãi thu được là: .

Số giờ làm việc của máy là: .

Số giờ làm việc của công nhân là: .

Một ngày máy làm việc không quá 15 giờ, nhân công làm việc không quá 8 giờ nên ta có hệ: $\left\{ \begin{matrix} 3x + 3y \leq 15 \\ 2x + y \leq 8 \\ x \geq 0 \\ y \geq 0 \end{matrix} \right.$ . Bài toán phát biểu như sau:

Tìm sao cho tại đó biểu thức đạt giá trị lớn nhất, với các ràng buộc: $\left\{ \begin{matrix} 3x + 3y \leq 15 \\ 2x + y \leq 8 \\ x \geq 0 \\ y \geq 0 \end{matrix} \right.$ .

Miền nghiệm của hệ bất phương trình là miền tứ giác kể cả các cạnh không bị gạch trong hình bên dưới.

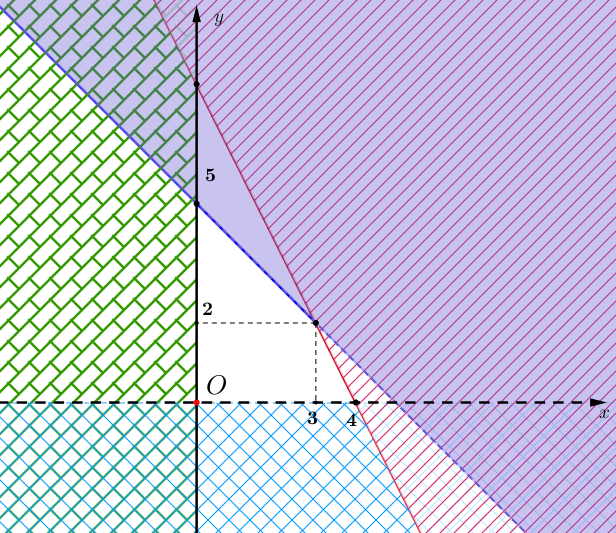
Xét các cặp : $\left\{ \begin{matrix} (x;y) = (0;0) \Rightarrow T = 0 \\ (x;y) = (4;0) \Rightarrow T = 20 \\ (x;y) = (3;2) \Rightarrow T = 23 \\ (x;y) = (0;5) \Rightarrow T = 20 \end{matrix} \right.\ \Rightarrow T_{\max} = 23$ .

Bài tập 2: Một phân xưởng sản xuất hai loại sản phẩm. Thời gian để làm ra một sản phẩm loại I gấp hai lần thời gian làm ra một sản phẩm loại II. Nếu chỉ sản xuất toàn sản phẩm loại II thì trong 1 giờ phân xưởng làm được 60 sản phẩm. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 sản phẩm loại I và 240 sản phẩm loại II. Tiền lãi khi bán một sản phẩm loại I là 24 nghìn đồng, một sản phẩm loại II là 15 nghìn đồng. Khi tiền lãi lớn nhất, tổng số sản phẩm loại I và loại II là bao nhiêu?

Hướng dẫn giải

Gọi số sản phẩm loại I và loại II mà phân xưởng làm được trong một ngày lần lượt là và $x,y \in \mathbb{N}^{*}$ .

Thời gian làm một sản phẩm loại II là $\frac{1}{60}$ .

Thời gian làm một sản phẩm loại I là $\frac{1}{30}$ .

Tổng thời gian làm sản phẩm loại I và sản phẩm loại II là $\frac{x}{30} + \frac{y}{60}$ .

Vì phân xưởng làm 8 tiếng mỗi ngày nên ta có $\frac{x}{30} + \frac{y}{60} \leq 8$ hay $2x + y \leq 480$ .

Tổng số tiền lãi khi bán sản phẩm loại I và sản phẩm loại II là .

Theo giả thiết ta có $0 \leq x \leq 200$ , $0 \leq y \leq 240$ .

Từ , và ta có hệ bất phương trình: $\left\{ \begin{matrix} 2x + y \leq 480 \\ 0 \leq x \leq 200 \\ 0 \leq y \leq 240 \end{matrix} \right.$ và $(x,y) \in \mathbb{N}^{*}$ .

Bài toán được phát biểu như sau:

Tìm sao cho tại đó biểu thức đạt giá trị lớn nhất, với các ràng buộc: $\left\{ \begin{matrix} 2x + y \leq 480 \\ 0 \leq x \leq 200 \\ 0 \leq y \leq 240 \end{matrix} \right.$ và $(x,y) \in \mathbb{N}^{*}$ .

Ta có miền nghiệm của hệ là miền ngũ giác với , , , , .

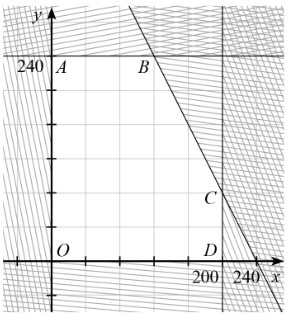
Ta có đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác .

Với ta có .

Vậy khi tiền lãi lớn nhất, số sản phẩm loại I là 120 sản phẩm và số sản phẩm loại II là 240 sản phẩm. Tổng là 360.

Điểm thỏa mãn cả ba bất phương trình , , nên miền nghiệm của hệ bất phương trình là miền được tô màu. Kể cả các đường thẳng $d_{1},\ d_{2},\ d_{3}$ .

Gọi là giao điểm của $d_{2}$ và $d_{3}$ .

là giao điểm của $d_{1}$ và $d_{2}$ .

là giao điểm của $d_{1}$ và $d_{3}$ .

Tại $\Rightarrow M = 2x + y = - 9$ .

Tại $\Rightarrow M = 2x + y = 1$ .

Tại $\Rightarrow M = 2x + y = 6$ .

Vậy $M_{\max} = 6$ .

------------------------------------------------------

Việc thành thạo bài toán quy hoạch tuyến tính hai biến giúp học sinh tăng tốc độ làm bài, hạn chế sai sót và nâng cao khả năng đạt điểm tối đa trong các câu hỏi Toán 12 ôn thi THPT Quốc gia.

Xem thử Tải về

Chọn file muốn tải về: