Xét tính đơn điệu của hàm số
Xét tính đồng biến, nghịch biến của hàm số
Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, VnDoc xin mời các bạn tham khảo tài liệu Xét tính đơn điệu của hàm số. Bộ tài liệu hướng dẫn chi tiết xét sự đồng biến, nghịch biến trên tập xác định bằng nhiều cách như dùng định nghĩa, định lí, giải nhanh bằng máy tính Casio, ... được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và ma trận đề thi THPT Quốc gia. Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.
- Tìm m để hàm số đồng biến, nghịch biến trên R
- 300 câu hỏi trắc nghiệm môn Toán lớp 12 (Có đáp án)
- Bài tập trắc nghiệm cực trị của hàm số và điểm uốn (Có đáp án)
- Bài tập trắc nghiệm tính đơn điệu của hàm số
- Câu hỏi trắc nghiệm môn Toán lớp 12: Cực trị của hàm số
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 12, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 12 sau: Nhóm Tài liệu học tập lớp 12. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Xét tính đơn điệu của hàm số mức độ nhận biết, thông hiểu
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
A. Xét tính đơn điệu của hàm số bằng định nghĩa
Cho hàm số y = f(x) xác định trên một khoảng K
+ Hàm số y = f(x) đồng biến trên K nếu 
\(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
+ Hàm số y = f(x) nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Hàm số đồng biến hoặc nghịch biến trên K được gọi là đơn điệu trên K
B. Xét tính đơn điệu của hàm số cho trước bằng đạo hàm
Bước 1: Tìm tập xác định của hàm số y = f(x)
Bước 2: Tính đạo hàm f’(x)
Bước 3: Tìm các điểm x0 sao cho f’(x0) = 0 hoặc f’(x0) không xác định.
Bước 4: Lập bảng xét dấu và đưa ra kết luận.
C. Xét tính đơn điệu của hàm số bằng máy tính Casio Fx570
Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính, quan sát kết quả nhận được để kết luận khoảng đồng biến, nghịch biến.
D. Bài tập ví dụ minh họa
Bài tập 1: Cho hàm số y = f(x) xác định và liên tục trên khoảng \(\left( { - \infty ; + \infty } \right)\), có bảng biến thiên như hình vẽ dưới đây.
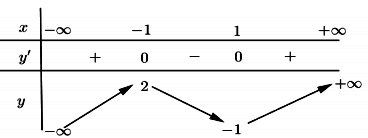
Hàm số đồng biến trên các khoảng nào trong các khoảng dưới đây?
| A. \(\left( { - \infty ;1} \right)\) |
B. \(\left( { - \infty ; - 1} \right)\) |
C. \(\left( { - 1;1} \right)\) |
D. \(\left( { - 1; + \infty } \right)\) |
Hướng dẫn giải
Quan sát bảng biến thiên ta thấy
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right);\left( {1, + \infty } \right)\)
Đáp án B
Bài tập 2: Kết luận nào sau đây đúng về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x + 1}}\)?
A. Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\)
B. Hàm số đồng biến trên \(\mathbb{R}\)
C. Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\)
D. Hàm số nghịch biến trên \(\mathbb{R}\)
Hướng dẫn giải
Công thức tính nhanh đạo hàm của hàm số \(y = \frac{{ax + b}}{{cx + d}} \Rightarrow y' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
Ta có: \(y' = \frac{1}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \ne 1\)
Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\)
Chọn đáp án A
Bài tập 3: Hàm số \(y = \frac{{{x^2} - 6x + 10}}{{x - 3}}\) nghịch biến trên các khoảng nào?
| A. \(\left( { - \infty ;2} \right)\) và \(\left( {4; + \infty } \right)\) |
B. \(\left( { - \infty ;1} \right)\) và \(\left( {5; + \infty } \right)\) |
| C. \(\left( {1;3} \right)\) và \(\left( {3;5} \right)\) |
D. \(\left( {2;3} \right)\) và \(\left( {3;4} \right)\) |
Hướng dẫn giải
Sử dụng phương pháp đạo hàm trên máy tính Casio để tìm đáp án sai, loại đáp án
Bước 1: Nhập Casio: 
Bước 2: CALC với x = 10 và x = 1,5
CALC x = 10 ta được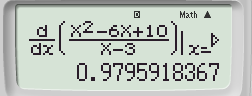 
⇒Loại được hai đáp án A và B
CALC x = 1,5 ta được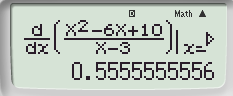 
⇒Loại được hai đáp án C
Đáp án D
Bài tập 4: Cho hàm số \(y = \left( {x - 3} \right)\sqrt {{x^2} + 1}\). Hàm số đồng biến trên các khoảng nào sau đây?
| A. \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\) |
B. \(\left( { - \infty ;\frac{1}{2}} \right)\) và \(\left( {1; + \infty } \right)\) |
| C. \(\left( {\frac{1}{2};1} \right)\) |
D. \(\left( {0;1} \right)\) |
Hướng dẫn giải
Bước 1: Nhập Casio: 
Bước 2: CALC với x = -100 và x = 0
CALC x = -100 ta được 
⇒Loại được hai đáp án C và D
CALC x = 0 ta được 
⇒Loại được hai đáp án A
Đáp án B
E. Bài tập tự rèn luyện
- Để củng cố kiến thức bài học VnDoc mời bạn đọc tham khảo thêm tài liệu:
Bài tập Xét tính đơn điệu của hàm số
--------------------------------------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Tính đơn điệu của hàm số Toán 12. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Thi THPT Quốc gia môn Toán, Thi THPT Quốc gia môn Văn, Thi THPT Quốc gia môn Lịch sử mà VnDoc tổng hợp và đăng tải.
