VnDoc.com

Cách tính khoảng cách từ điểm đến đường thẳng

Khoảng cách trong không gian

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Tính khoảng cách từ điểm đến đường thẳng trong Oxyz

A. Phương trình đường thẳng
B. Khoảng cách từ điểm M đến đường thẳng Δ
- Công thức tính khoảng cách từ điểm đến đường thẳng
C. Bài tập tính khoảng cách từ điểm đến đường thẳng
D. Bài tập tự rèn luyện có đáp án

Trong các bài toán khoảng cách trong không gian, việc nắm vững cách tính khoảng cách từ điểm đến đường thẳng là kỹ năng quan trọng, thường xuyên xuất hiện trong chương trình Toán THPT và các đề kiểm tra – thi cử. Nếu không xác định đúng phương pháp, học sinh rất dễ nhầm lẫn giữa khoảng cách trong mặt phẳng và trong không gian. Bài viết này sẽ giúp bạn tiếp cận cách tính một cách rõ ràng, dễ hiểu và áp dụng hiệu quả vào từng dạng bài cụ thể.

A. Phương trình đường thẳng

Cho đường thẳng $\Delta$ $\Delta$ đi qua điểm $M_{0}\left( x_{0};y_{0};z_{0} \right)$ $M_{0}\left( x_{0};y_{0};z_{0} \right)$ và nhận vectơ $\overrightarrow{a\ } = \left( a_{1};a_{2};a_{3} \right)$ $\overrightarrow{a\ } = \left( a_{1};a_{2};a_{3} \right)$ với ${a_{1}}^{2} + {a_{2}}^{2} + {a_{3}}^{2} \neq 0$ ${a_{1}}^{2} + {a_{2}}^{2} + {a_{3}}^{2} \neq 0$ làm vectơ chỉ phương. Khi đó $\Delta$ $\Delta$ có phương trình tham số là:

$\left\{ \begin{matrix} x = x_{0} + a_{1}t \\ y = y_{0} + a_{2}t \\ z = z_{0} + a_{2}t \\ \end{matrix} \right.\ ;\ \left( t\mathbb{\in R} \right)$ $\left\{ \begin{matrix} x = x_{0} + a_{1}t \\ y = y_{0} + a_{2}t \\ z = z_{0} + a_{2}t \\ \end{matrix} \right.\ ;\ \left( t\mathbb{\in R} \right)$

Cho đường thẳng $\Delta$ $\Delta$ đi qua điểm $M_{0}\left( x_{0};y_{0};z_{0} \right)$ $M_{0}\left( x_{0};y_{0};z_{0} \right)$ và nhận vectơ $\overrightarrow{a\ } = \left( a_{1};a_{2};a_{3} \right)$ $\overrightarrow{a\ } = \left( a_{1};a_{2};a_{3} \right)$ sao cho $a_{1}a_{2}a_{3} \neq 0$ $a_{1}a_{2}a_{3} \neq 0$ làm vectơ chỉ phương. Khi đó $\Delta$ $\Delta$ có phương trình chính tắc là:

$\frac{x - x_{0}}{a_{1}} = \frac{y - y_{0}}{a_{2}} = \frac{z - z_{0}}{a_{3}}$ $\frac{x - x_{0}}{a_{1}} = \frac{y - y_{0}}{a_{2}} = \frac{z - z_{0}}{a_{3}}$

B. Khoảng cách từ điểm M đến đường thẳng Δ

Công thức tính khoảng cách từ điểm đến đường thẳng

$\Delta$ $\Delta$ đi qua điểm $M_{0}$ $M_{0}$ và có vectơ chỉ phương $\overrightarrow{a_{\Delta}}$ $\overrightarrow{a_{\Delta}}$

$\boxed{d(M,\Delta) = \frac{\left| \left\lbrack \overrightarrow{a_{\Delta}},\overrightarrow{M_{0}M} \right\rbrack \right|}{\left| \overrightarrow{a_{\Delta}} \right|}}$ $\boxed{d(M,\Delta) = \frac{\left| \left\lbrack \overrightarrow{a_{\Delta}},\overrightarrow{M_{0}M} \right\rbrack \right|}{\left| \overrightarrow{a_{\Delta}} \right|}}$

C. Bài tập tính khoảng cách từ điểm đến đường thẳng

Ví dụ. a. Trong không gian $Oxyz$, cho điểm $A(2;1;1)$ và đường thẳng $d:\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{- 2}$ $d:\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{- 2}$. Tính khoảng cách từ A đến đường thẳng d.

b. Trong không gian với hệ tọa độ $Oxyz$, khoảng cách từ điểm $M(2; - 4; - 1)$ tới đường thẳng $\Delta:\left\{ \begin{matrix} x = t \\ y = 2 - t \\ z = 3 + t \\ \end{matrix} \right.$ $\Delta:\left\{ \begin{matrix} x = t \\ y = 2 - t \\ z = 3 + t \\ \end{matrix} \right.$ bằng bao nhiêu?

Hướng dẫn giải

a.Gọi $M(1;\ 2;\ 3) \in d$ $M(1;\ 2;\ 3) \in d$

$\Rightarrow AM = ( - 1;1;2) \Rightarrow \left\lbrack \overrightarrow{AM};\overrightarrow{u} \right\rbrack = ( - 6;0; - 3)$ $\Rightarrow AM = ( - 1;1;2) \Rightarrow \left\lbrack \overrightarrow{AM};\overrightarrow{u} \right\rbrack = ( - 6;0; - 3)$

Ta có $d(A;d) = \frac{\left| \left\lbrack \overrightarrow{AM};\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{3\sqrt{5}}{3} = \sqrt{5}$ $d(A;d) = \frac{\left| \left\lbrack \overrightarrow{AM};\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{3\sqrt{5}}{3} = \sqrt{5}$.

b. Đường thẳng $\Delta$ $\Delta$ đi qua $N(0;2;3)$, có véc-tơ chỉ phương $\overrightarrow{u} = (1; - 1;2)$ $\overrightarrow{u} = (1; - 1;2)$.

Ta có $\overrightarrow{MN} = ( - 2;6;4)$ $\overrightarrow{MN} = ( - 2;6;4)$ và $\left\lbrack \overrightarrow{MN},\overrightarrow{u} \right\rbrack = (16;8; - 4)$ $\left\lbrack \overrightarrow{MN},\overrightarrow{u} \right\rbrack = (16;8; - 4)$.

Vậy khoảng cách từ $M$ đến đường thẳng $\Delta$ $\Delta$ là:

$d(M;\Delta) = \frac{\left| \left\lbrack \overrightarrow{MN},\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{\sqrt{336}}{\sqrt{6}} = 2\sqrt{14}$ $d(M;\Delta) = \frac{\left| \left\lbrack \overrightarrow{MN},\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{\sqrt{336}}{\sqrt{6}} = 2\sqrt{14}$

Ví dụ. Trong không gian với hệ toạ độ $Oxyz$, cho $(P):x - 2y + 2z - 5 = 0,$$A( - 3;0;1),B(1; -1;3)$. Viết phương trình đường thẳng $d$ qua $A$, song song với $(P)$ sao cho khoảng cách từ $B$ đến $d$ là lớn nhất.

Hướng dẫn giải

Hình vẽ minh họa

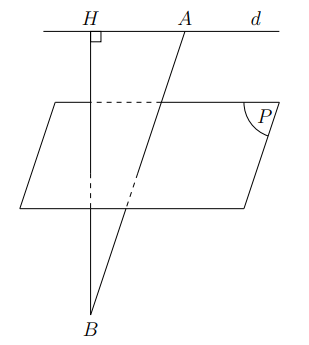
Vì $( - 3 - 2\ .0 + 2\ .1 - 5).\left( 1 - 2.( - 1) + 2.3 - 5 \right) < 0$ $( - 3 - 2\ .0 + 2\ .1 - 5).\left( 1 - 2.( - 1) + 2.3 - 5 \right) < 0$ nên hai điểm A, B khác phía so với (P).

Gọi H là hình chiếu của B lên d.

Ta có: BH ≤ BA nên khoảng cách BH từ B đến d lớn nhất khi và chỉ khi H trùng A.

Khi đó AB ⊥ d.

VTPT của (P) là $\overrightarrow{n} = (1; - 2;2),\overrightarrow{AB} = (4; - 1;2)$ $\overrightarrow{n} = (1; - 2;2),\overrightarrow{AB} = (4; - 1;2)$

VTCP của d là $\overrightarrow{u} = \left\lbrack \overrightarrow{n};\overrightarrow{AB} \right\rbrack = ( - 2;6;7)$ $\overrightarrow{u} = \left\lbrack \overrightarrow{n};\overrightarrow{AB} \right\rbrack = ( - 2;6;7)$

Mà d qua A(−3; 0; 1) nên phương trình đường thẳng d là: $\frac{x + 3}{2} = \frac{y}{- 6} = \frac{z - 1}{- 7}$ $\frac{x + 3}{2} = \frac{y}{- 6} = \frac{z - 1}{- 7}$

Ví dụ. Trong không gian $Oxyz$, cho điểm $A(0;1;1)$ và hai đường thẳng $d_{1}:\left\{ \begin{matrix} x = - 1 \\ y = - 1 + t \\ z = t \\ \end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)$ $d_{1}:\left\{ \begin{matrix} x = - 1 \\ y = - 1 + t \\ z = t \\ \end{matrix} \right.\ ;\left( t\mathbb{\in R} \right)$ và $d_{2}:\frac{x - 1}{3} = \frac{y - 2}{1} = \frac{z}{1}$ $d_{2}:\frac{x - 1}{3} = \frac{y - 2}{1} = \frac{z}{1}$. Gọi $d$ là đường thẳng đi qua điểm $A$, cắt đường thẳng $d_{1}$ $d_{1}$ và vuông góc với đường thẳng $d_{2}$ $d_{2}$. Đường thẳng $d$ đi qua điểm nào trong các điểm dưới đây?

A. $N(2;1; - 5)$	B. $Q(3;2;5)$
C. $P( - 2; - 3;11)$	D. $M(1;0; - 1)$

Hướng dẫn giải

Gọi $\left\{ \begin{matrix} B = d_{1} \cap d \\ B \in d_{1} \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} B( - 1; - 1 + t;t) \\ \overrightarrow{AB} = ( - 1;t - 2;t - 1) \\ \end{matrix} \right.$ $\left\{ \begin{matrix} B = d_{1} \cap d \\ B \in d_{1} \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} B( - 1; - 1 + t;t) \\ \overrightarrow{AB} = ( - 1;t - 2;t - 1) \\ \end{matrix} \right.$

$d_{2}$ $d_{2}$ có một vectơ chỉ phương $\overrightarrow{u} = (3;1;1)$ $\overrightarrow{u} = (3;1;1)$.

Do $d\bot d_{2}$ $d\bot d_{2}$ nên $\overrightarrow{u}.\overrightarrow{AB} = 0 \Leftrightarrow - 3 + t - 2 + t - 1 = 0$ $\overrightarrow{u}.\overrightarrow{AB} = 0 \Leftrightarrow - 3 + t - 2 + t - 1 = 0$

$\Leftrightarrow t = 3 \Rightarrow \overrightarrow{AB} = ( - 1;1;2)$ $\Leftrightarrow t = 3 \Rightarrow \overrightarrow{AB} = ( - 1;1;2)$

Ta có: $\left\{ \begin{matrix} \overrightarrow{AN} = (2;0;6);\overrightarrow{AQ} = (3;1;4) \\ \overrightarrow{AP} = ( - 2; - 4;10);\overrightarrow{AM} = (1; - 1; - 2) \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \overrightarrow{AN} = (2;0;6);\overrightarrow{AQ} = (3;1;4) \\ \overrightarrow{AP} = ( - 2; - 4;10);\overrightarrow{AM} = (1; - 1; - 2) \\ \end{matrix} \right.$

Suy ra đường thẳng $d$ đi qua $M$.

D. Bài tập tự rèn luyện có đáp án

Bài 1. Trong không gian với hệ tọa độ $Oxyz,$ cho đường thẳng $d:\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z}{- 1}$ $d:\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z}{- 1}$. Viết phương trình đường thẳng $\Delta$ $\Delta$ đi qua điểm $A(2;3; - 1)$ cắt $d$ tại $B$ sao cho khoảng cách từ $B$ đến mặt phẳng $(\alpha):x + y + z - 1 = 0$ $(\alpha):x + y + z - 1 = 0$ bằng $2\sqrt{3}$ $2\sqrt{3}$.

Bài 2. Trong không gian với hệ tọa độ $Oxyz,$ cho mặt phẳng $(P):x - 2y + 2z - 5 = 0$ và hai điểm $A( - 3;0;1),\ B(1; - 1;3).$ $A( - 3;0;1),\ B(1; - 1;3).$ Trong các đường thẳng đi qua $A$ và song song với $(P)$, đường thẳng mà khoảng cách từ $B$ đến đường thẳng đó là nhỏ nhất có phương trình là gì?

Bài 3. Trong không gian với hệ tọa độ $\left\{ \begin{matrix} x = 62t \\ y = - 25t \\ z = - 2 + 61t \\ \end{matrix} \right.$ $\left\{ \begin{matrix} x = 62t \\ y = - 25t \\ z = - 2 + 61t \\ \end{matrix} \right.$ cho đường thẳng $d:\frac{x - 3}{2} = \frac{y + 2}{1} = \frac{z + 1}{- 1}$ $d:\frac{x - 3}{2} = \frac{y + 2}{1} = \frac{z + 1}{- 1}$, mặt phẳng $(P):x + y + z + 2 = 0$ . Gọi $M$ là giao điểm của $d$ và $(P)$. Gọi $\Delta$ $\Delta$ là đường thẳng nằm trong $(P)$ vuông góc với $d$ và cách $M$ một khoảng bằng $\sqrt{42}$ $\sqrt{42}$. Viết phương trình đường thẳng $(P)$?

Tài liệu còn dài, mời bạn đọc tải tài liệu tham khảo đầy đủ của chúng tôi!

----------------------------------------------------

Hiểu đúng cách tính khoảng cách từ điểm đến đường thẳng không chỉ giúp giải nhanh các bài toán khoảng cách trong không gian mà còn tạo nền tảng vững chắc cho những chuyên đề hình học nâng cao. Khi áp dụng đúng công thức và phương pháp, việc xử lý các bài toán liên quan sẽ trở nên chính xác và hiệu quả hơn, góp phần nâng cao kết quả học tập và khả năng làm bài thi.

Tải về

Chọn file muốn tải về: