VnDoc.com

Các dạng toán thống kê Toán 9

Chuyên đề Toán 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề Toán 9: Thống kê

A. Bài tập thống kê
B. Bài tập tự rèn luyện

Bạn đang tìm hiểu về các dạng toán thống kê toán 9? Bài viết này sẽ giúp bạn hệ thống hóa kiến thức, phân loại các dạng bài tập thường gặp như: tính số trung bình cộng, tần số, biểu đồ và phân tích dữ liệu. Với ví dụ minh họa rõ ràng và phương pháp giải chi tiết, bạn sẽ dễ dàng làm chủ đề chuyên môn này trong chương trình Toán lớp 9.

A. Bài tập thống kê

Bài 1. Sau khi thống kê độ dài (đơn vị: centimét) của 60 lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:

Nhóm	$\lbrack 10;20)$ $\lbrack 10;20)$	$\lbrack 20;30)$ $\lbrack 20;30)$	$\lbrack 30;40)$ $\lbrack 30;40)$	$\lbrack 40;50)$ $\lbrack 40;50)$	Cộng
Tần số (n)	7	16	27	10	60

Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm $\lbrack 30;40)$ $\lbrack 30;40)$.

Hướng dẫn giải

Tần số ghép nhóm $\lbrack 30;40)$ $\lbrack 30;40)$ là 27

Tần số tương đối ghép nhóm của nhóm $\lbrack 30;40)$ $\lbrack 30;40)$ là: $\frac{27.100}{60}\% = 45\%$ $\frac{27.100}{60}\% = 45\%$

Bài 2. Sau khi điều tra mật độ dân số ( đơn vị: người/km²) của 37 tỉnh, thành phố thuộc các vùng Bắc Trung Bộ và Duyên hải miền Trung, Tây Nguyên, Đông Nam Bộ, Đồng bằng sông Cửu Long (không kể Thành phố Hồ Chí Minh) ở năm 2021, người ta có biểu đồ tần số ghép nhóm dưới đây:

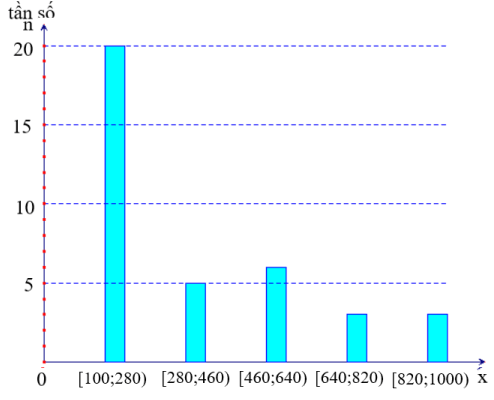
a) Tìm tần số ghép nhóm của nhóm $\lbrack 460;640)$ $\lbrack 460;640)$

b) Tính tần số tương đối ghép nhóm của nhóm $\lbrack 100;280)$ $\lbrack 100;280)$.

Hướng dẫn giải

a) Tần số ghép nhóm của nhóm $\lbrack 460;640)$ $\lbrack 460;640)$là 6.

b) Tần số tương đối ghép nhóm của nhóm $\lbrack 100;280)$ $\lbrack 100;280)$là $f = \frac{20}{37}.100\% \approx 54\%$ $f = \frac{20}{37}.100\% \approx 54\%$.

Bài 3. Đo chiều cao (đơn vị là cm) của học sinh lớp 9A cho kết quả như sau;

156 157 164 166 166 165 157 154 155 158 160

163 163 161 162 159 159 160 160 160 159 158

160 160 158 163 162 162 162 161 162 161 163

161 163 161 164 166 165 165

Hãy lập bảng tần số ghép nhóm với các nhóm [155; 158), [158; 161), [161; 164), [164;167).

Tính tần số tương đối của nhóm [161; 164)

Hướng dẫn giải

Bảng tần số ghép nhóm

Chiều cao (cm)	[155; 158)	[158; 161)	[161; 164)	[164;167)
Số HS	5	12	15	8

Tần số tương đối của nhóm [161; 164) là : $\frac{15}{40}$ $\frac{15}{40}$. 100% = 37,5%

Bài 4. Kết quả đo tốc độ của $25$ xe ô tô (đơn vị: $km/h$) khi đi qua một trạm quan sát đã được thống kê dưới bảng sau

$46$	$55$	$57$	$50$	$45$
$41$	$44$	$46$	$40$	$58$
$50$	$56$	$52$	$59$	$44$
$52$	$40$	$42$	$47$	$54$
$45$	$48$	$58$	$49$	$40$

a) Hãy ghép các số liệu thành bốn nhóm ứng với bốn nửa khoảng có độ dài bằng nhau.

b) Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm ở câu a.

Hướng dẫn giải

a) Trong mẫu số liệu trên, số liệu có giá trị nhỏ nhất là $41$, số liệu có giá trị lớn nhất là $59$. Vì thế, ta có thể chọn nửa khoảng $\lbrack 40;\ \ 60)$ $\lbrack 40;\ \ 60)$ sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng $\lbrack 40;\ \ 60)$ $\lbrack 40;\ \ 60)$. Vì độ dài của nửa khoảng $\lbrack 40;\ \ 60)$ $\lbrack 40;\ \ 60)$ bằng $60 - 40 = 20$ nên ta có thể phân chia nửa khoảng đó thành bốn nửa khoảng có độ dài bằng nhau là: $\lbrack 40;\ \ 45)$ $\lbrack 40;\ \ 45)$, $\lbrack 45;\ \ 50)$ $\lbrack 45;\ \ 50)$, $\ \lbrack 50;\ \ 55)\ \lbrack 55;\ \ 60)$ $\ \lbrack 50;\ \ 55)\ \lbrack 55;\ \ 60)$.

Vậy ta có thể ghép mẫu số liệu đã cho theo bốn nhóm ứng với bốn nửa khoảng đó.

b) Tốc độ của xe đi từ $40$ $km/h$ đến dưới $45$ $km/h$ là $7$ xe;

Tốc độ của xe đi từ $45$ $km/h$ đến dưới $50$ $km/h$ là $7$ xe;

Tốc độ của xe đi từ $50$ $km/h$ đến dưới $55$ $km/h$ là $5$ xe;

Tốc độ của xe đi từ $55$ $km/h$ đến dưới $60$ $km/h$ là $6$ xe.

Do đó ta có bảng tần số ghép nhóm

Tốc độ $(km/h)$	$\lbrack 40;\ 45)$ $\lbrack 40;\ 45)$	$\lbrack 45;\ 50)$ $\lbrack 45;\ 50)$	$\lbrack 50;\ 55)$ $\lbrack 50;\ 55)$	$\lbrack 55;\ 60)$ $\lbrack 55;\ 60)$
Tần số	$7$	$7$	$5$	$6$

Bài 5. Sau khi điều tra cân nặng ( đơn vị: kg) của$200$ học sinh khối lớp 4 của một trường tiểu học, người ta có biểu đồ tần số tương đối ghép nhóm dưới đây:

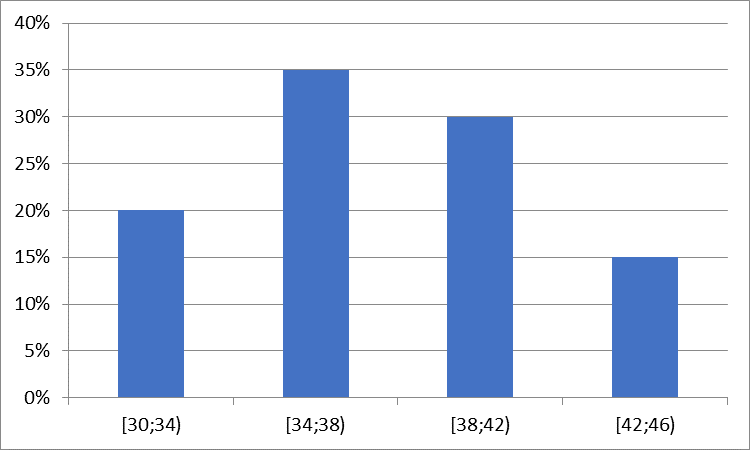
Lập bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ. Tìm tần số ghép nhóm của nhóm $\lbrack 38;42)$ $\lbrack 38;42)$

Hướng dẫn giải

Bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ là :

Cân nặng ( kg)	$\left\lbrack 30 \right.$ $\left\lbrack 30 \right.$; $\left. \ 34 \right)$ $\left. \ 34 \right)$	$\left\lbrack 34 \right.$ $\left\lbrack 34 \right.$; $\left. \ 38 \right)$ $\left. \ 38 \right)$	$\left\lbrack 38 \right.$ $\left\lbrack 38 \right.$; $\left. \ 42 \right)$ $\left. \ 42 \right)$	$\left\lbrack 42 \right.$ $\left\lbrack 42 \right.$; $\left. \ 46 \right)$ $\left. \ 46 \right)$
Tần số tương đối	20%	35%	30%	15%

Tần số ghép nhóm của nhóm $\left\lbrack 38 \right.$ $\left\lbrack 38 \right.$; $\left. \ 42 \right)$ $\left. \ 42 \right)$ là :200. 30% = 60.

Bài 6. Thống kê tuổi thọ của $30$ bóng đèn điện được lắp thử (đơn vị: giờ) được cho trong bảng dưới dây:

$1180$	$1150$	$1190$	$1170$	$1180$	$1170$	$1160$	$1170$	$1160$	$1150$
$1190$	$1180$	$1170$	$1170$	$1170$	$1190$	$1170$	$1170$	$1170$	$1180$
$1170$	$1160$	$1160$	$1160$	$1170$	$1160$	$1180$	$1180$	$1150$	$1170$

a. Lập bảng tần số và tần số tương đối của mẫu số liệu trên.

b. Có người nói: “Có trên $75\%$ $75\%$ bóng đèn có tuổi thọ từ $1160$ đến $1180$”. Theo em nhận định đó đúng hay sai?

2) Bình tung một đồng tiền xu có hai mặt sấp (S) và ngửa (N) liên tiếp ba lần, sau mỗi lần tung Bình đều ghi lại mặt xuất hiện. Tính xác suất của các biến cố A: “Mặt sấp xuất hiện đúng một lần”.

Hướng dẫn giải

1) a) Liệt kê các giá trị khác nhau ta được: $1150;\ 1160;\ 1170;\ 1180;\ 1190$ $1150;\ 1160;\ 1170;\ 1180;\ 1190$

Với mỗi giá trị khác nhau, ta đếm xem giá trị đó xuất hiện bao nhiêu lần trong bảng.

Bảng phân bố tần số:

Tuổi thọ (giờ)	$1150$	$1160$	$1170$	$1180$	$1190$	Tổng
Tần số $n$	$6$	$3$	$12$	$6$	$3$	$N = 30$

Tần số tương đối của các giá trị lần lượt là:

$f_{1} = \frac{3.100}{30} = 10\%$ $f_{1} = \frac{3.100}{30} = 10\%$; $f_{2} = \frac{6.100}{30} = 20\%$ $f_{2} = \frac{6.100}{30} = 20\%$; $f_{3} = \frac{12.100}{30} = 40\%$ $f_{3} = \frac{12.100}{30} = 40\%$;

$f_{4} = \frac{6.100}{30} = 20\%$ $f_{4} = \frac{6.100}{30} = 20\%$; $f_{5} = \frac{3.100}{30} = 10\%$ $f_{5} = \frac{3.100}{30} = 10\%$

Vì vậy, bảng tần số tương đối của mẫu số liệu đã cho được nêu trong Bảng sau.

Tuổi thọ (giờ)	$1150$	$1160$	$1170$	$1180$	$1190$	Tổng
Tần số tương đối $\%$ $\%$	$10$	$20$	$40$	$20$	$10$	$100$

b) Số bóng đèn có tuổi thọ từ $1160$ đến $1180$ chiếm số phần trăm là:

$20\% + 40\% + 20\% = 80\%$ $20\% + 40\% + 20\% = 80\%$

Vậy nhận định “Có trên $75\%$ $75\%$ bóng đèn có tuổi thọ từ $1160$ đến $1180$” là đúng.

2) Xét phép thử “Tung một đồng tiền xu liên tiếp ba lần”. Ta thấy, các kết quả có thể xảy ra của phép thử đó là đồng khả năng.

Có 8 khả năng có thể xảy ra là: SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN.

Có 3 kết quả thuận lợi cho biến cố A là: SNN; NSN; NNS.

Vậy $P(A) = \frac{3}{8}.$ $P(A) = \frac{3}{8}.$

B. Bài tập tự rèn luyện

Bài 1. Khảo sát đánh giá của khách hàng về chất lượng một loại dịch vụ mới, số liệu được biểu diễn trong biểu đồ sau:

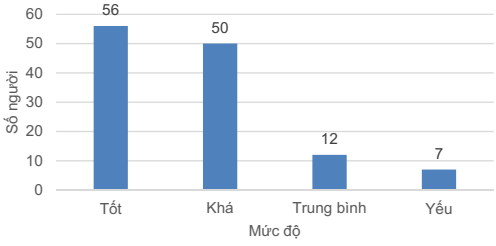
a) Lập bảng tần số tương đối cho mẫu số liệu.

b) Vẽ biểu đồ tần số tương đối dạng biểu đồ hình quạt tròn biểu diễn dữ liệu.

Bài 2. Cân nặng của các bạn học sinh lớp 9A (đơn vị: ki-lo-gam) có kết quả như sau:

$62$	$59$	$68$	$53$	$50$	$57$	$72$	$65$	$62$	$58$
$69$	$53$	$64$	$67$	$72$	$74$	$63$	$56$	$66$	$66$
$62$	$52$	$65$	$69$	$60$	$52$	$65$	$63$	$74$	$68$
$59$	$68$	$64$	$69$	$56$	$72$	$67$	$58$	$62$	$60$

Mẫu số liệu thống kê ở trên đã được ghép thành năm nhóm ứng với năm nửa khoảng: $\lbrack 50\ \ ;\ \ 55)$ $\lbrack 50\ \ ;\ \ 55)$, $\lbrack 55\ \ ;\ \ 60)$ $\lbrack 55\ \ ;\ \ 60)$, $\lbrack 60\ \ ;\ \ 65)$ $\lbrack 60\ \ ;\ \ 65)$, $\lbrack 65\ \ ;\ \ 70)$ $\lbrack 65\ \ ;\ \ 70)$, $\lbrack 70\ \ ;\ \ 75)$ $\lbrack 70\ \ ;\ \ 75)$. Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm ở trên.

Bài 3. Chỉ số phát triển con người (HDI) là chỉ tiêu tổng hợp phản ánh các mặt thu nhập, sức khỏe, giáo dục của người dân trong một quốc gia. Các nước và vùng lãnh thổ trên thế giới được chia thành 4 nhóm theo HDI: Nhóm 1(rất cao) có HDI từ 0,8 trở lên; Nhóm 2(cao) có HDI từ 0,7 đến dưới 0,8; Nhóm 3(trung bình) có HDI từ 0,55 đến dưới 0,7; Nhóm 4(thấp) có HDI dưới 0,55. Năm 2021, chỉ số HDI của 11 quốc gia Đông Nam Á như sau.

0,939 0,829 0,803 0,8 0,705 0,703 0,699 0,607 0,607 0,593 0,585

Dựa vào dữ liệu trên, hãy hoàn thành bảng tần số ghép nhóm sau:

Chỉ số HDI	$\lbrack 0;\ 0,55)$ $\lbrack 0;\ 0,55)$	$\lbrack 0,55;\ 0,7)$ $\lbrack 0,55;\ 0,7)$	$\lbrack 0,7;\ 0,8)$ $\lbrack 0,7;\ 0,8)$	$\lbrack 0,8;\ 1)$ $\lbrack 0,8;\ 1)$	Cộng
Tần số	?	?	?	?	N =

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

----------------------------------------

Trên đây là tổng hợp các thống kê toán học dạng thường gặp trong Toán 9 cùng với các phương pháp giải và ví dụ minh họa cụ thể. Bài thi nắm chắc từng dạng bài sẽ giúp bạn tự tin hơn khi làm bài kiểm tra cũng như ôn thi vào lớp 10. Hãy luyện tập thường xuyên để thành công hơn và đạt kết quả cao nhé!

Tải về

Chọn file muốn tải về: