Bài toán xác định hệ số hàm trùng phương khi biết đồ thị có đáp án chi tiết
Xác định hệ số a, b, c, d của hàm trùng phương
Trong chương trình Toán 12, chuyên đề hàm số trùng phương là phần kiến thức trọng tâm, xuất hiện thường xuyên trong các đề kiểm tra và đề thi THPT Quốc gia. Một trong những dạng bài nâng cao quen thuộc là bài toán xác định hệ số của hàm trùng phương khi biết đồ thị.
Bài viết này sẽ giúp bạn hiểu rõ bản chất của hệ số a, b, c, d trong hàm trùng phương, cách dựa vào đồ thị để suy ra hệ số chính xác, cùng với đáp án chi tiết và lời giải minh họa dễ hiểu. Đây là tài liệu ôn tập hữu ích giúp học sinh rèn kỹ năng nhận diện và xử lý bài toán hàm trùng phương nhanh – chính xác – chuẩn đề thi THPT Quốc gia môn Toán.
A. Cách xác định hệ số hàm trùng phương từ đồ thị
Xác định hệ số 
\(a,\ b,\ c\) của hàm số \(y = ax^{4} + bx^{2} + c\) dựa vào BBT, đồ thị.
Hàm số: \(y = ax^{4} + bx^{2} + c\ \ (a
\neq 0)\).
Xác định hệ số \(a\):
- Hướng đồ thị bên phải đi lên thì \(a >
0\). Hướng đồ thị bên phải đi xuống thì \(a < 0\).
Xác định hệ số \(b\): (Dựa vào hệ số \(a\) để kết luận)
- Đồ thị hàm số có 3 điểm cực trị thì \(a.b
< 0\). Đồ thị hàm số có 1 điểm cực trị thì \(a.b \geq 0\).
Xác định hệ số \(c\): Đồ thị cắt trục \(Oy\) tại điểm \(A(0;c)\).
- Điểm \(A(0;c)\) nằm phía trên trục \(Ox\) thì \(c > 0\). Điểm \(A(0;c)\) nằm phía dưới trục \(Ox\) thì \(c <
0\).
- Điểm \(A(0;c)\) trùng với gốc tọa độ \(O(0;0)\) thì \(c = 0\).
Hình vẽ minh họa
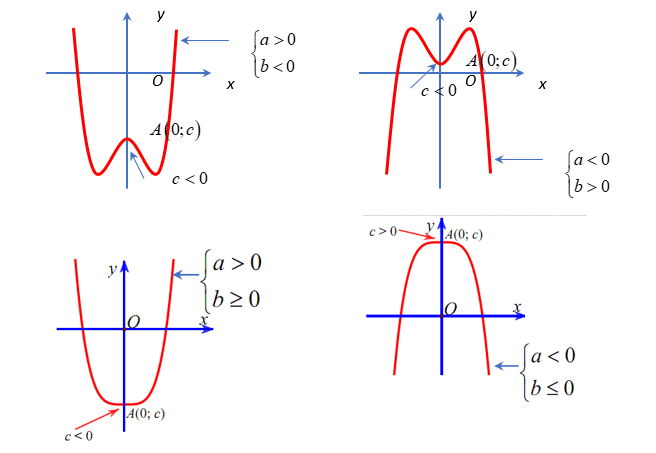
B. Ví dụ minh họa xác định hệ số hàm trùng phương
Ví dụ 1. Để đồ thị hàm số \(y = ax^{4} +
bx^{2} + c\ \ (a \neq 0)\) có bảng biến thiên như hình vẽ sau:
Khẳng định nào sau đây là đúng?
A. \(\left\{ \begin{matrix}
a < 0 \\
b \geq 0
\end{matrix} \right.\). B. \(\left\{
\begin{matrix}
a > 0 \\
b \geq 0
\end{matrix} \right.\). C. \(\left\{ \begin{matrix}
a > 0 \\
b \leq 0
\end{matrix} \right.\). D. \(\left\{
\begin{matrix}
a < 0 \\
b \leq 0
\end{matrix} \right.\).
Hướng dẫn giải
Chọn B
Từ bảng biến thiên ta thấy đồ thị hàm số có nhánh bên phải đi lên và có một cực trị
\(\Rightarrow \left\{ \begin{matrix}
a > 0 \\
ab \geq 0
\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}
a > 0 \\
b \geq 0
\end{matrix} \right.\).
Ví dụ 2. Cho hàm số \(y = ax^{4} + bx^{2} +
c\ \ (a \neq 0)\) có đồ thị như hình vẽ.
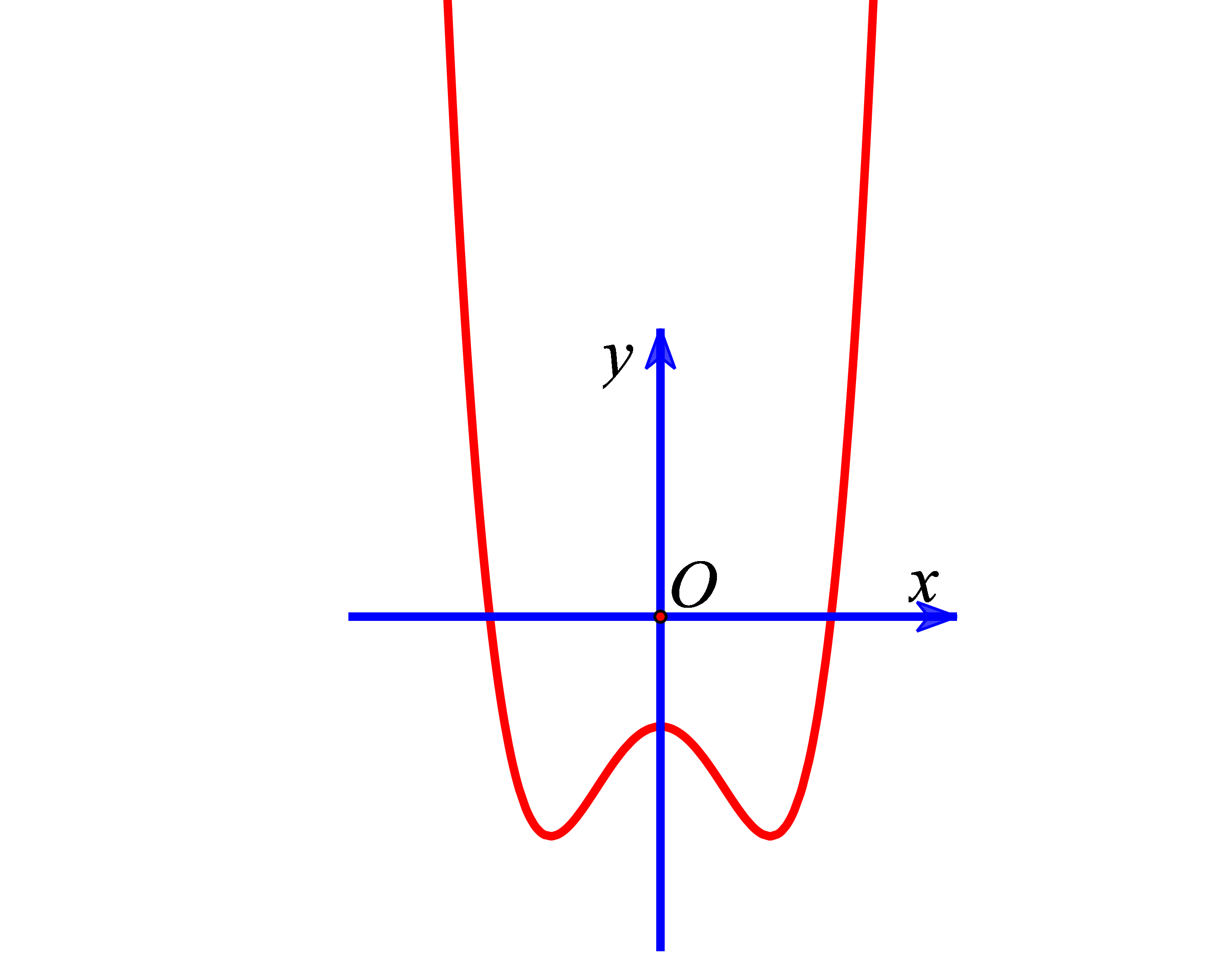
Kết luận nào sau đây là đúng?
A. \(a > 0;b > 0;c < 0\). B. \(a > 0;b < 0;c < 0\).
C. \(a > 0;b < 0;c > 0\). D. \(a < 0;b > 0;c < 0\).
Hướng dẫn giải
Chọn B
Đồ thị hàm số có nhánh bên phải đi lên và có 3 cực trị \(\Rightarrow \left\{ \begin{matrix}
a > 0 \\
b < 0
\end{matrix} \right.\).
Đồ thị cắt \(Oy\) tại điểm \((0;c)\) nằm bên dưới trục \(Ox \Rightarrow c < 0\).
Ví dụ 3. Cho hàm số \(y = ax^{4} + bx^{2} +
c\ \ (a \neq 0)\) có đồ thị như hình vẽ.
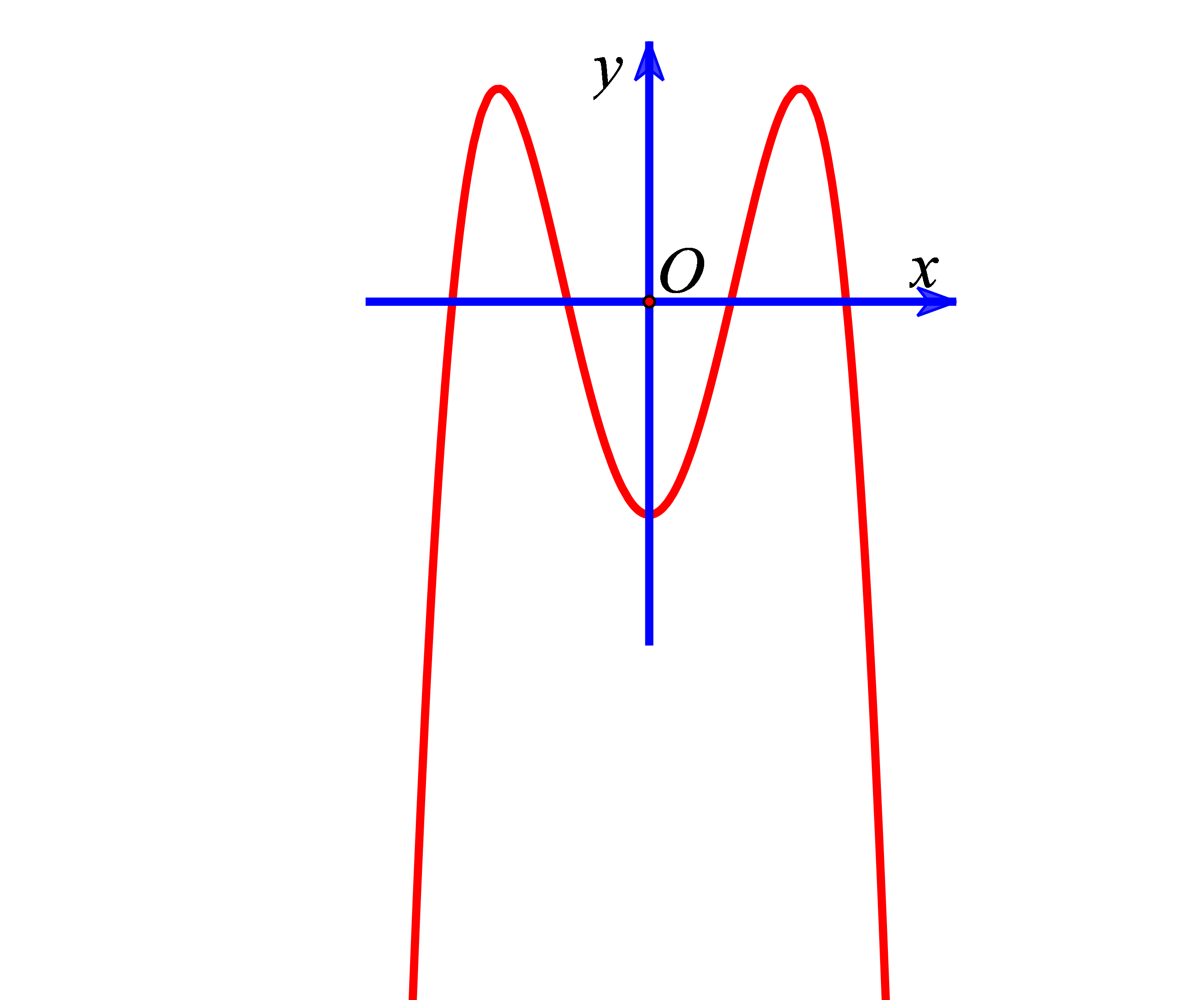
Kết luận nào sau đây là đúng?
A. \(a > 0;b < 0;c > 0\). B. \(a < 0;b > 0;c < 0\).
C. \(a < 0;b < 0;c < 0\). D. \(a > 0;b < 0;c < 0\).
Hướng dẫn giải
Chọn B
Đồ thị hàm số có nhánh bên phải đi xuống và có 3 cực trị \(\Rightarrow \left\{ \begin{matrix}
a < 0 \\
b > 0
\end{matrix} \right.\).
Đồ thị cắt \(Oy\) tại điểm \((0;c)\) nằm bên dưới trục \(Ox \Rightarrow c < 0\).
Ví dụ 4. Cho hàm số \(y = ax^{4} + bx^{2} +
c\ \ (a \neq 0)\) có đồ thị như hình vẽ.
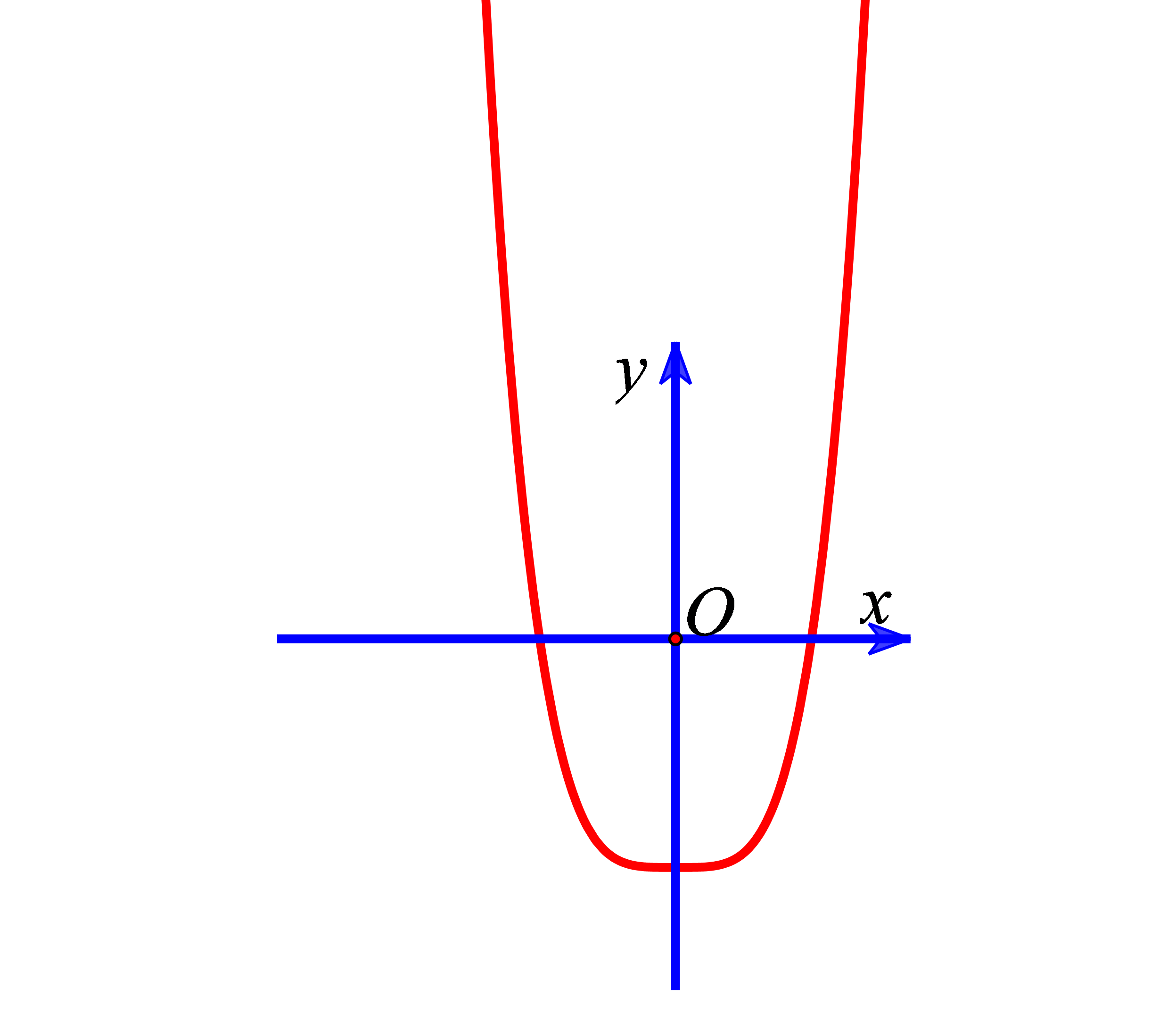
Kết luận nào sau đây là đúng?
A. \(a < 0;b \geq 0;c < 0\). B. \(a > 0;b \geq 0;c < 0\).
C. \(a > 0;b > 0;c < 0\). D. \(a > 0;b \geq 0;c > 0\).
Hướng dẫn giải
Chọn B
Đồ thị hàm số có nhánh bên phải đi lên và có 1 cực trị \(\Rightarrow \left\{ \begin{matrix}
a > 0 \\
b \geq 0
\end{matrix} \right.\).
Đồ thị cắt \(Oy\) tại điểm \((0;c)\) nằm bên dưới trục \(Ox \Rightarrow c < 0\).
Ví dụ 5. Cho hàm số \(y = ax^{4} + bx^{2} +
c\ \ (a \neq 0)\) có đồ thị như hình bên.
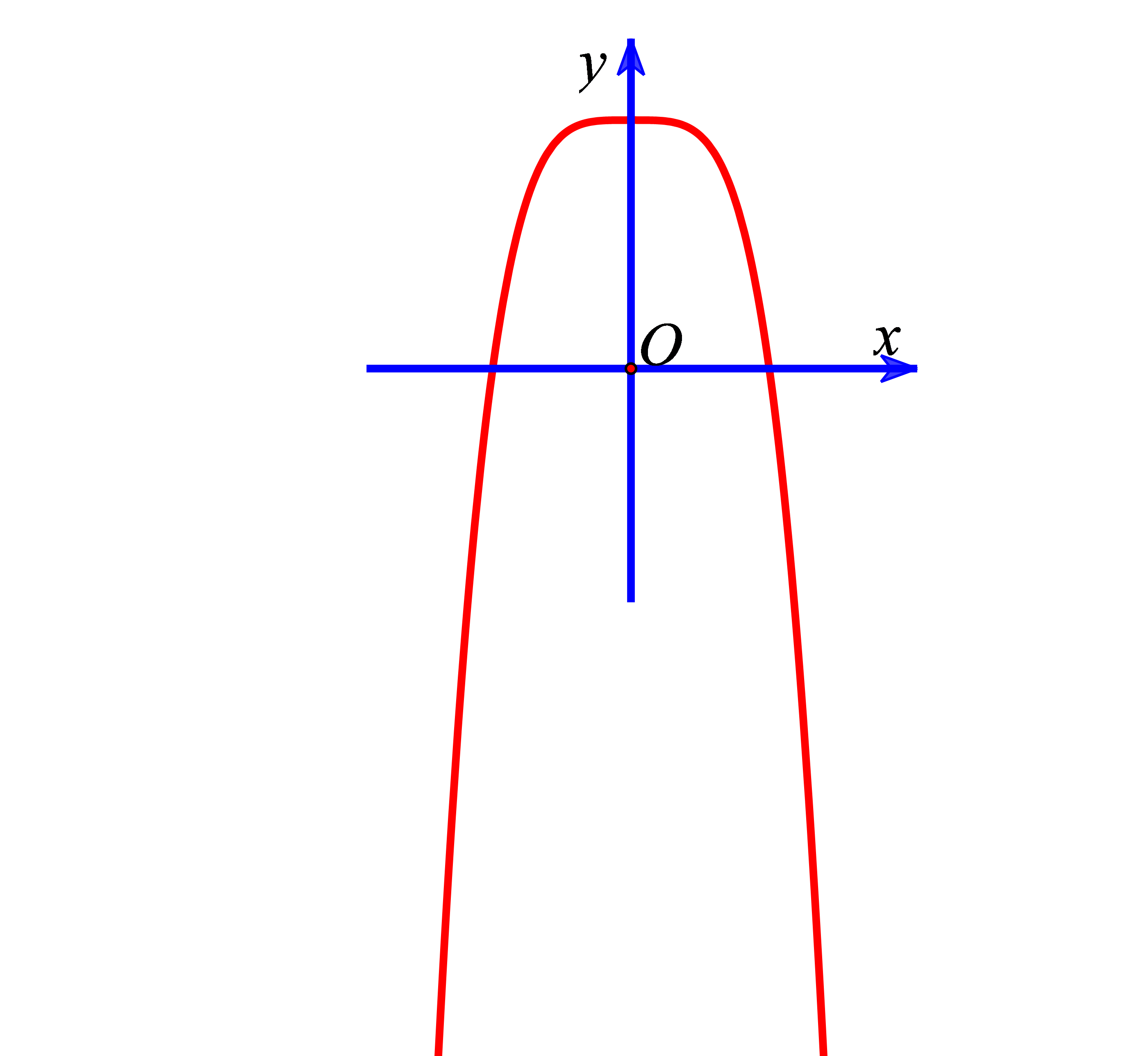
Kết luận nào sau đây là đúng?
A. \(a < 0;b \leq 0;c > 0\). B. \(a < 0;b < 0;c > 0\).
C. \(a > 0;b > 0;c > 0\). D. \(a < 0;b \leq 0;c < 0\).
Hướng dẫn giải
Chọn A
Đồ thị hàm số có nhánh bên phải đi xuống và có 1 cực trị \(\Rightarrow \left\{ \begin{matrix}
a < 0 \\
b \leq 0
\end{matrix} \right.\).
Đồ thị cắt \(Oy\) tại điểm \((0;c)\) nằm trên \(Ox \Rightarrow c > 0\).
C. Bài tập tự rèn luyện khảo sát hàm số trùng phương có đáp án chi tiết
Bài tập 1. Cho hàm số \(y = f(x) = ax^{4} +
bx^{2} + c\) có bảng biến thiên như hình vẽ dưới đây:
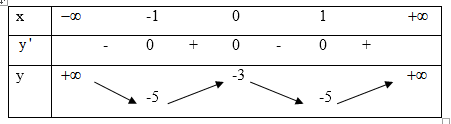
Tính giá trị của biểu thức \(P = a + 2b +
3c\)
A. \(P = - 15\). B. \(P = 8\).
C. \(P = 15\). D. \(P = - 8\).
Bài tập 2. Biết rằng hàm số \(y = f(x) =
ax^{4} + bx^{2} + c\) có đồ thị là đường cong trong hình vẽ bên dưới.
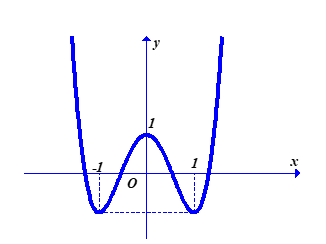
Tính giá trị \(f(a + b + c)\).
A. \(f(a + b + c) = - 2\). B. \(f(a + b + c) = 2\).
C. \(f(a + b + c) = - 1\). D. \(f(a + b + c) = 1\).
Bài tập 3. Đồ thị hàm số \(y = ax^{4} +
bx^{2} + c\) cắt trục hoành tại bốn điểm phân biệt \(A\), \(B\), \(C\), \(D\) như hình vẽ bên. Biết rằng \(AB = BC =
CD\), mệnh đề nào sau dây đúng?
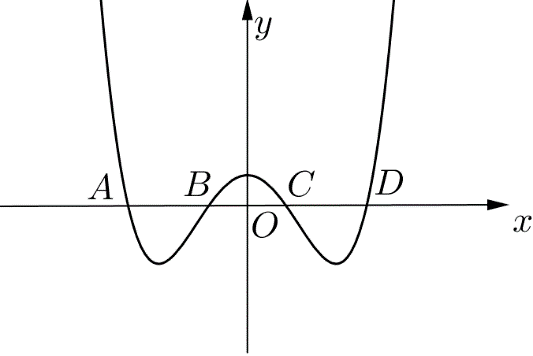
A. \(a > 0,b < 0,c > 0,100b^{2} =
9ac\). B. \(a > 0,b > 0,c > 0,9b^{2} =
100ac\).
C. \(a > 0,b < 0,c > 0,9b^{2} =
100ac\). D. \(a > 0,b > 0,c > 0,100b^{2} =
9ac\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
-----------------------------------------------------------
Qua bài viết Bài toán xác định hệ số hàm trùng phương khi biết đồ thị có đáp án chi tiết, bạn đã nắm được cách sử dụng thông tin từ đồ thị để xác định hệ số của hàm số trùng phương một cách chính xác. Hãy luyện thêm nhiều bài tập hàm trùng phương có đáp án và lời giải chi tiết để củng cố kiến thức, tăng tốc độ làm bài và đạt điểm cao trong kỳ thi THPT Quốc gia môn Toán sắp tới.
