Chuyên đề Toán 9: Đa giác đều

Chuyên đề Toán 9: Đa giác đều là một trong những phần kiến thức hình học quan trọng trong chương trình Toán lớp 9, thường xuyên xuất hiện trong các đề thi học kỳ và đề thi vào lớp 10. Bài viết này sẽ giúp bạn hệ thống lại toàn bộ kiến thức lý thuyết về đa giác đều như: định nghĩa, tính chất, công thức tính góc, cạnh, diện tích, cùng với các dạng bài tập minh họa có lời giải chi tiết. Đây sẽ là tài liệu hữu ích giúp bạn học nhanh – nhớ lâu – vận dụng tốt vào bài thi.

A. Tính chất đa giác đều Toán 9

I. Đa giác là gì?

Trong đa giác \(ABCDE\) ờ hình vẽ:

- Các đỉnh là các điểm \(A,B,C,D,E\);

- Các cạnh là các đoạn thảng \(AB,BC,CD,DE,EA\);

- Các cặp đỉnh kề nhau là: \(A\) và \(B,\) \(B\) và \(C,\) \(C\) và \(D,\) \(D\) và \(E,\) \(E\) và \(A\);

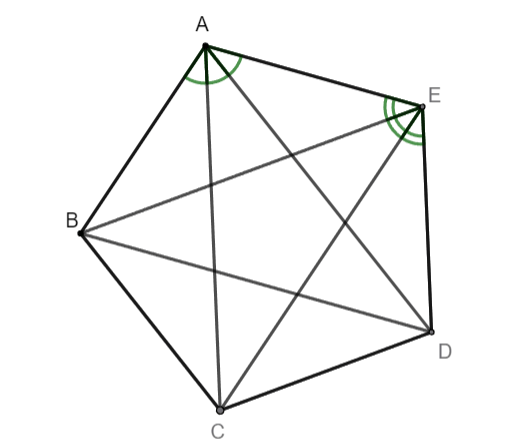
- Các đường chéo là các đoạn thả̉ng nối hai dỉnh không kể nhau: \(AC\), \(AD,BD,BE,CF\);

- Các góc là: \(\widehat{ABC},\ \ \widehat{BCD},\ \ \widehat{CDE},\ \ \widehat{DEA},\ \ \widehat{EAB}\).

Đa giác có \(n\) đỉnh \((n \geq 3)\) được gọi là hình \(n -\) giác hay hình \(n\) cạnh.

Ta thường gọi các đa giác có \(3,4,5,6,8\) đỉnh là tam giác, tứ giác, ngũ giác, lục giác, bát giác.

II. Đa giác đều là gì?

- Đa giác lổi là đa giác luôn nằm vể một phía của đường thẳng chứa một cạnh bất kì của đa giác.

- Đa giác đều là một đa giác lồi có cạnh bằng nhau và các góc bằng nhau.

B. Các dạng bài tập đa giác đều lớp 9

Dạng I. Nhận dạng đa giác đều

Bài toán 1. Tìm các đa giác lồi trong hình vẽ và giải thích.

Hướng dẫn giải

Các đa giác trong hình \(a,c\), e là các đa giác lồi vì đa giác luôn nằm vể một phía của đường thẳng chứa một cạnh bất kì của đa giác.

Đa giác ở hình \(b\) không phải là đa giác lồi vì không cùng nằm về một phía so với đường thẳng \(AD\) hoặc \(BC\).

Hình d cũng không phải là đa giác lồi và không cùng nằm về một phía so với đường thẳng \(BC\) hoặc \(CD\)

Bài toán 2. Tìm và gọi tên các đa giác đều có trong hình vẽ dưới đây.

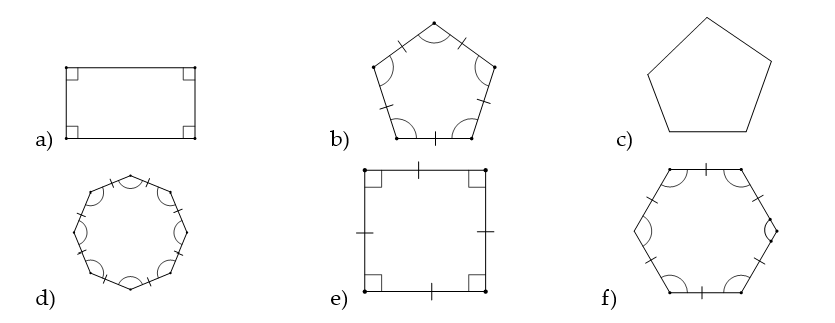
Hướng dẫn giải

Hình \(3\ b\) là ngũ giác đều;

Hình \(3\ d\) là bát giác đều;

Hình \(3e\) là tứ giác đều;

Hình \(3\ g\) là lục giác đều.

Dạng II. Tính toán

Bài toán 3. Cho ngũ giác \(ABCDE\) có các cạnh bằng nhau và \(\widehat{A} = \widehat{B} = \widehat{C} = 108{^\circ}\). Ngũ giác \(ABCDE\) có phải là ngũ giác đều không?

Hướng dẫn: Để chứng minh ngũ giác \(ABCDE\) đều ta phải chứng minh:

• Các cạnh bằng nhau (giả thiết đã cho).
• Các góc bằng nhau: \(\widehat{D} = \widehat{E} = 108{^\circ}\).

Hướng dẫn giải

Ta có: \(AB = BC = CD = DE = EA(gt)\left( \ ^{*} \right)\)

Xét tam giác \(ABE\) có \(AB = AE\) (gt)

nên \(\Delta ABE\) cân tại \(A\) có \(\widehat{A} = 108{^\circ}(gt)\)

\(\Rightarrow \widehat{B_{1}} = \widehat{E_{1}} = \frac{180{^\circ} - \widehat{A}}{2} = \frac{180{^\circ} - 108{^\circ}}{2} = 36{^\circ}\)

Tương tự với tam giác \(BCD\), ta có: \(\widehat{B_{3}} = \widehat{D_{1}} = 36{^\circ}\)

Lại có \(\widehat{ABC} = \widehat{B_{1}} + \widehat{B_{2}} + \widehat{B_{3}} = 108{^\circ}\)

\(\Rightarrow \widehat{B_{2}} = 108{^\circ} - \left( \widehat{B_{1}} + \widehat{B_{3}} \right) = 108{^\circ} - (36{^\circ} + 36{^\circ}) = 36{^\circ}\)

Dễ thấy \(\Delta ABE = \Delta CBD\) (c.g.c)

\(\Rightarrow BE = BD\) hay tam giác \(EBD\) cân tại \(B\) có \(\widehat{B_{2}} = 36{^\circ}\)

\({\widehat{E}}_{2} = {\widehat{D}}_{2} = \frac{180{^\circ} - {\widehat{B}}_{2}}{2} = \frac{180{^\circ} - 36{^\circ}}{2} = 72{^\circ}\)

Khi đó \(\widehat{AED} = \widehat{E_{1}} + \widehat{E_{2}} = 36{^\circ} + 72{^\circ} = 108{^\circ}\)

Tương tự \(\widehat{CDE} = 108{^\circ}\)

Vây \(\widehat{A} = \widehat{B} = \widehat{C} = \widehat{D} = \widehat{E} = 108{^\circ}\left( \ ^{**} \right)\)

Từ \(\left( \ ^{*} \right)\) và \(\left( \ ^{**} \right) \Rightarrow\) ngũ giác \(ABCDE\) là ngũ giác đều (Các cạnh bằng nhau, các góc bằng nhau).

Bài toán 4. Cho hình tròn \((O;R)\).

a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên \((O;R)\).

b) Tính các cạnh của các hình vừa vẽ theo \(R\).

Hướng dẫn giải

a) Vẽ tam giác đều \(ABC\) nội tiếp đường tròn \((O;R)\)

Vẽ đường cao \(AH\), ta có: \(AB = AC;OB = OC = R\)

Nên \(A,O,H\) thuộc đường trung trực của \(BC\) vì \(\Delta ABC\) đều nên \(O\) là trọng tâm của tam giác.

Ta có \(AH = \frac{3}{2}AO = \frac{3}{2}R(1)\) (tính chất trọng tâm)

Lại có \(AH\) là đường cao của tam giác \(ABC\) đều nên \(AH = \frac{AB\sqrt{3}}{2}\)

Từ (1) và (2) \(\Rightarrow \frac{3}{2}R = \frac{AB\sqrt{3}}{2} \Rightarrow AB = \frac{3R}{\sqrt{3}} = \sqrt{3} \cdot R\)

Vậy cạnh của tam giác đều nội tiếp đường tròn \((O;R)\) là \(\sqrt{3}\). R.

-Vẽ hình vuông \(ABCD\) nội tiếp đường tròn \((O;R)\)

Ta có: \(AC\bot BD\) (tính chất hai đường chéo hình vuông)

Xét tam giác \(AOB\) vuông tại \(O\).

Theo định lí Pythgore, ta có: \(AB^{2} = OA^{2} + OB^{2} = R^{2} + R^{2} = 2R^{2}\)

\(\Rightarrow AB = \sqrt{2R^{2}} = R\sqrt{2}.\)

Vậy cạnh của hình vuông nội tiếp đường tròn \((O;R)\) là \(R\sqrt{2}\).

-Vẽ lục giác đều \(ABCDEF\) nội tiếp đường tròn \((O;R)\)

Vì \(ABCDEF\) là lục giác đều \(\Rightarrow AB = BC = CD = DE = EF = FA\)

\(\Rightarrow sd\widehat{AB} = sd\widehat{BC} = sd\widehat{CD} = sd\widehat{DE} = sd\widehat{EF} = sd\widehat{FA}\)

\(\Rightarrow \widehat{AOB} = \widehat{BOC} = \widehat{COD} = \widehat{DOE} = \widehat{EOF} = \widehat{FOA} = \frac{360}{6} = 60{^\circ}\)

Xét tam giác \(AOB\) cân tại \(O\) có \(\widehat{AOB} = 60{^\circ}\) nên \(\Delta AOB\) đều \(\Rightarrow AB = R\).

Chứng minh tương tự, ta có \(BC = CD = DE;EF = FA = AB = R\).

Vậy cạnh của hình lục giác đều nội tiếp đường tròn \((O;R)\) là \(R\).

Ghi nhớ: Bán kính đường tròn ngoại tiếp là \(R\).

- Độ dài cạnh tam giác đều nội tiếp là \(R\sqrt{3}\)

- Độ dài cạnh hình vuông nội tiếp là \(R\sqrt{2}\).

- Độ dài cạnh hình lục giác đều nội tiếp

C. Bài tập vận dụng Đa giác đều có lời giải

Bài toán 1. Cho đường tròn \((O;R)\). Lấy các điểm \(A,B,C,D,E,F\) trên đường tròn \((O;R)\) sao cho số đo các cung \(\widehat{AB},\) \(\widehat{BC},\) \(\widehat{DE},\) \(\widehat{EF},\) \(\widehat{FA}\) bằng nhau. Đa giác \(ABCDEF\) có là đa giác đều không?

Bài toán 2. Cho ngũ giác đều \(ABCDE\) như hình vẽ.

a) Tính tổng các góc trong của tam giác \(ABC,ACD,ADE\), từ đó suy ra các góc trong ngũ giác đều \(ABCED\).

b) Tính số đo góc E.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-----------------------------------------------

Trên đây là toàn bộ nội dung chuyên đề Đa giác đều Toán 9, bao gồm lý thuyết trọng tâm và bài tập điển hình có hướng dẫn giải chi tiết. Mong rằng tài liệu này sẽ hỗ trợ bạn ôn tập hiệu quả và nắm chắc kiến thức về đa giác đều. Đừng quên luyện tập thường xuyên và kết hợp với các chuyên đề hình học khác để nâng cao kỹ năng giải Toán. Chúc bạn học tốt và đạt điểm cao trong kỳ thi sắp tới!