Chuyên đề Toán 9: Góc nội tiếp
Cách giải bài toán góc nội tiếp lớp 9
Chào mừng bạn đến với chuyên đề Toán 9: Góc nội tiếp – một chủ điểm quan trọng và thường xuyên xuất hiện trong các đề kiểm tra, đề thi vào lớp 10. Trong bài viết này, chúng ta sẽ cùng tìm hiểu đầy đủ lý thuyết, các tính chất quan trọng, cách vận dụng vào bài tập, và hệ thống các dạng bài thường gặp về góc nội tiếp. Nội dung được trình bày rõ ràng, dễ hiểu, phù hợp với học sinh lớp 9 đang ôn tập hoặc muốn nâng cao kiến thức hình học.
A. Ôn thi vào 10 với chuyên đề góc nội tiếp Toán 9
1. Góc nội tiếp là gì?
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong gọi là cung bị chắn.

2. Định lí
Trong một đường tròn số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
3. Hệ quả
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng ![]() ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Các dạng bài tập góc nội tiếp lớp 9
Dạng I. Tính số đo góc
Bài toán 1. Cho các điểm như hình vẽ. Tính số đo các góc của tam giác ![]() , biết rằng
, biết rằng ![]()
![]() .
.

Hướng dẫn giải
Xét đường tròn ![]() , ta có:
, ta có:
Vì góc nội tiếp ![]() và góc ở tâm
và góc ở tâm ![]() cùng chắn cung nhỏ
cùng chắn cung nhỏ ![]()
nên ![]()
Vì góc nội tiếp ![]() và góc ở tâm
và góc ở tâm ![]() cùng chắn cung nhỏ
cùng chắn cung nhỏ ![]() nên
nên ![]()
Xét tam giác ![]() , ta có:
, ta có:
![]()
![]()
![]() .
.
Bài toán 2. Cho đường tròn ![]() và hai dây cung
và hai dây cung ![]() cắt nhau tại
cắt nhau tại ![]() (hình vẽ). Tính số đo góc
(hình vẽ). Tính số đo góc ![]() , biết rằng
, biết rằng ![]() và
và ![]() .
.
Hướng dẫn giải
Hình vẽ minh họa:

Do hai góc nội tiếp ![]() và
và ![]() cùng chắn cung
cùng chắn cung ![]() nên
nên ![]() .
.
Tương tự ![]() và
và ![]() cùng chắn cung
cùng chắn cung ![]() nên
nên ![]() .
.
Xét tam giác ![]() có:
có: ![]()
![]()
![]()
![]() .
.
Ta có: ![]() (kề bù)
(kề bù)
![]()
![]()
Bài toán 3. Tính số đo các góc ![]() và cung lớn
và cung lớn ![]() trong hình vẽ.
trong hình vẽ.

Hướng dẫn giải
Xét đường tròn ![]() , ta có:
, ta có:
Do hai góc nội tiếp ![]() và
và ![]() cùng chắn cung nhỏ
cùng chắn cung nhỏ ![]()
nên ![]() .
.
Vì góc nội tiếp ![]() và góc ở tâm
và góc ở tâm ![]() cùng chắn cung nhỏ
cùng chắn cung nhỏ ![]()
Nên ![]()
Sđ cung nhỏ ![]() : sđ
: sđ ![]() nên số đo cung lớn là: sđ
nên số đo cung lớn là: sđ ![]()
Bài toán 4. Ba điểm ![]() thuộc đường tròn
thuộc đường tròn ![]() sao cho
sao cho ![]() . Từ
. Từ ![]() vẽ
vẽ ![]() vuông góc với
vuông góc với ![]() và
và ![]() cắt đường tròn
cắt đường tròn ![]() tại
tại ![]() .
.
a. Tính ![]() ;
;
b. Gọi ![]() là một dây cung song song với dây
là một dây cung song song với dây ![]() . Tính
. Tính ![]() .
.
Hướng dẫn giải
Hình vẽ minh họa:
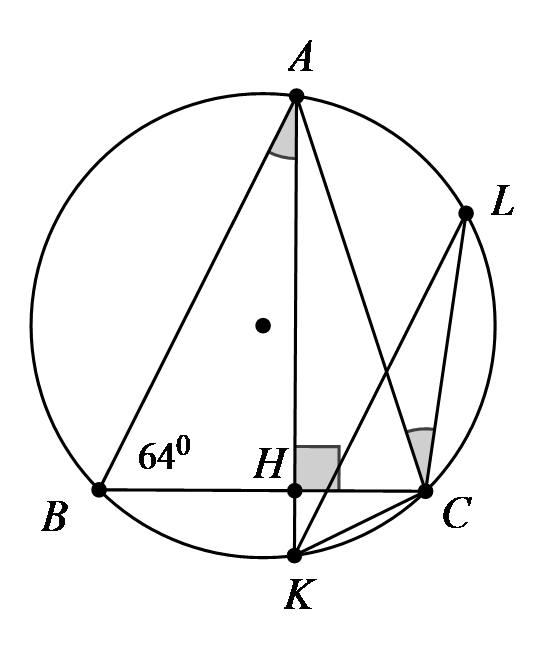
a. Ta có: ![]() (góc nội tiếp cùng chắn cung
(góc nội tiếp cùng chắn cung ![]() ).
).
Tam giác ![]() vuông tại
vuông tại ![]() (gt) có
(gt) có ![]() (gt)
(gt)
![]() (góc nội tiếp cùng chắn cung
(góc nội tiếp cùng chắn cung ![]() ).
).
b. Ta có: ![]() (1) (góc nội tiếp cùng chắn cung
(1) (góc nội tiếp cùng chắn cung ![]() ).
).
mà ![]() (2) (cặp góc so le trong)
(2) (cặp góc so le trong)
Từ (1) và (2) ![]()
Dạng II. Các bài toán chứng minh
Bài toán 5. Cho đường tròn ![]() và hai dây cung
và hai dây cung ![]() cắt nhau tại điểm
cắt nhau tại điểm ![]() nằm trong
nằm trong ![]() (Hình vẽ)
(Hình vẽ)

a. Biết rằng ![]() . Tính số đo của góc
. Tính số đo của góc ![]() .
.
b. Chứng minh rằng ![]()
Hướng dẫn giải
a. (Xem hình vẽ)
Xét đường tròn ![]() . Nối
. Nối ![]() với
với ![]() ta có góc nội tiếp
ta có góc nội tiếp ![]() và góc ở tâm cùng chắn cung nhỏ
và góc ở tâm cùng chắn cung nhỏ ![]() nên
nên ![]() .
.
Tương tự với góc nội tiếp ![]() và góc ở tâm
và góc ở tâm ![]() .
.
Ta có: ![]() .
.
Xét tam giác ![]() , ta có:
, ta có:
![]()
![]()
![]()
![]() (đối đỉnh)
(đối đỉnh)
b) Nối ![]() với
với ![]() với
với ![]() .
.
Xét tam giác ![]() và tam giác
và tam giác ![]() có
có ![]() và
và ![]() là hai góc nội tiếp cùng chắn cung nhỏ
là hai góc nội tiếp cùng chắn cung nhỏ ![]() nên
nên ![]() (*)
(*)
Tương tự ![]() và
và ![]() là hai góc nội tiếp cùng chắn cung nhỏ
là hai góc nội tiếp cùng chắn cung nhỏ ![]() nên
nên ![]()
Từ ![]() và
và ![]() (g.g)
(g.g)
![]()
![]() (đpcm)
(đpcm)
Bài toán 6. Cho đường tròn ![]() , đường kính
, đường kính ![]() và điểm
và điểm ![]() nằm ngoài
nằm ngoài ![]() . Cho hai đường thẳng
. Cho hai đường thẳng ![]() lần lượt cắt
lần lượt cắt ![]() tại
tại ![]() (khác
(khác ![]() ) và
) và ![]() (khác
(khác ![]() ). Gọi
). Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() (hình vē). Chứng minh rằng
(hình vē). Chứng minh rằng ![]() vuông góc với
vuông góc với ![]() .
.
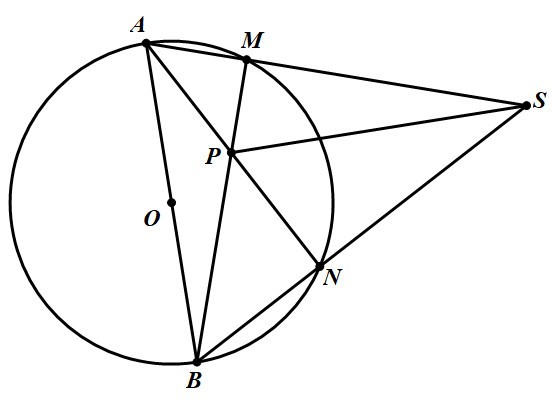
Hướng dẫn giải
a) (Xem hình vẽ).
Nối ![]() với
với ![]() với
với ![]()
Ta có ![]() hay
hay ![]()
Chứng minh tương tự, ta có tam giác ![]() vuông tại
vuông tại ![]()
![]() hay
hay ![]() và
và ![]() là hai đường cao của tam giác
là hai đường cao của tam giác ![]() . Mà
. Mà ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() nên
nên ![]() là trực tâm của tam giác
là trực tâm của tam giác ![]()
![]() . (điều phải chứng minh).
. (điều phải chứng minh).
Bài toán 7. Cho ![]() nội tiếp trong đường tròn (
nội tiếp trong đường tròn ( ![]() . Lấy
. Lấy ![]() trên cạnh
trên cạnh ![]() cắt cung
cắt cung ![]() ở
ở ![]() . Chứng minh rằng.
. Chứng minh rằng.
a) ![]() ;
;
b) ![]()
Hướng dẫn giải
a) Ta có: ![]() (góc nội tiếp cùng chắn
(góc nội tiếp cùng chắn ![]() ) và
) và ![]() (góc nội tiếp cùng chắn
(góc nội tiếp cùng chắn ![]() ) mà
) mà ![]() (vì
(vì ![]() )
)
Do đó ![]()
b) Xét ![]() và
và ![]() có:
có: ![]() (Chứng minh trên)
(Chứng minh trên) ![]() (góc nội tiếp cùng chắn
(góc nội tiếp cùng chắn ![]() )
)
Vậy ![]() (g.g)
(g.g) ![]() (điều phải chứng minh).
(điều phải chứng minh).
Bài toán 8. Cho ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]() , hai đường cao
, hai đường cao ![]() cắt nhau tại
cắt nhau tại ![]() .
. ![]() cắt đường tròn
cắt đường tròn ![]() tại
tại ![]() .
.
a) Chứng minh ![]() là tia phân giác của
là tia phân giác của ![]() .
.
b) Chứng minh ![]() đối xứng với
đối xứng với ![]() qua
qua ![]() .
.
Hướng dẫn giải
Hình vẽ minh họa:
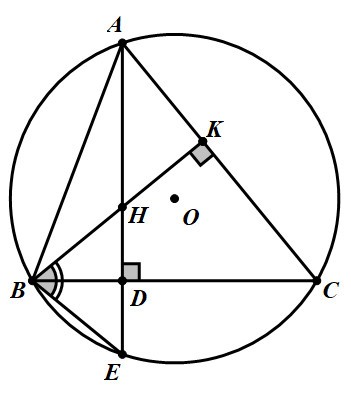
a) Ta có: ![]() (cùng phụ với
(cùng phụ với ![]() )
)
![]() (góc nội tiếp cùng chắn
(góc nội tiếp cùng chắn ![]() )
)
![]()
Chứng tỏ ![]() là phân giác của
là phân giác của ![]() .
.
b) ![]() có đường cao
có đường cao ![]() đồng thời là đường phân giác (chứng minh trên). Do đó
đồng thời là đường phân giác (chứng minh trên). Do đó ![]() cũng là đường trung trực của đoạn
cũng là đường trung trực của đoạn ![]() hay
hay ![]() và
và ![]() đối xứng nhau qua
đối xứng nhau qua ![]() .
.
Bài toán 9. Cho tam giác ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]() . Gọi
. Gọi ![]() là điểm chính giữa của cung nhỏ
là điểm chính giữa của cung nhỏ ![]() và
và ![]() là giao điểm của AJ với
là giao điểm của AJ với ![]() . Chứng minh rằng:
. Chứng minh rằng: ![]() .
.
Hướng dẫn giải
Hình vẽ minh họa:
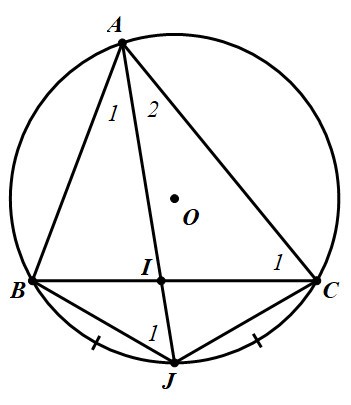
![]() là điểm chính giữa cung
là điểm chính giữa cung ![]()
![]() (g.g)
(g.g)
![]() (1)
(1)
Ta lại co: ![]() (góc nội tiếp cùng chắn cung
(góc nội tiếp cùng chắn cung ![]() ).
).
Do đó ![]() (g.g)
(g.g)
![]()
Từ (1) và (2) ![]()
Dạng III. Toán thực tế
Bài toán 10. Trên sân bóng, khi trái được đặt tại điểm phạt đền thì có góc sút bằng ![]() và trái bóng cách mỗi cọc gôn
và trái bóng cách mỗi cọc gôn ![]() Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền
Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền ![]() thì góc sút bằng bao nhiêu?
thì góc sút bằng bao nhiêu?
Hướng dẫn giải
Hình vẽ minh họa:

Gọi ![]() là chân hai cọc gôn và O là điểm phạt đền.
là chân hai cọc gôn và O là điểm phạt đền.
Ta có ![]()
Vậy ![]() nằm trên đường tròn tâm
nằm trên đường tròn tâm ![]() bán kính
bán kính ![]() và góc ở tâm
và góc ở tâm ![]()
Do đó, góc nội tiếp ![]()
Vậy góc sút bằng ![]()
C. Bài tập vận dụng góc nội tiếp lớp 9 có lời giải
Bài toán 1. Tính số đo của ![]() và
và ![]() trong hình vẽ.
trong hình vẽ.

Bài toán 2. Cho ![]() và
và ![]() là hai đường kính vuông góc của nửa đường tròn
là hai đường kính vuông góc của nửa đường tròn ![]() . Gọi
. Gọi ![]() lần lượt là hai điểm trên hai cung nhỏ
lần lượt là hai điểm trên hai cung nhỏ ![]() và chia mỗi cung đó thành hai cung bằng nhau (hình vẽ).
và chia mỗi cung đó thành hai cung bằng nhau (hình vẽ).

Tìm số đo các góc sau:
a. ![]() ; b.
; b. ![]() .
.
Bài toán 3. Tính số đo góc ![]() (xem hình vẽ).
(xem hình vẽ).
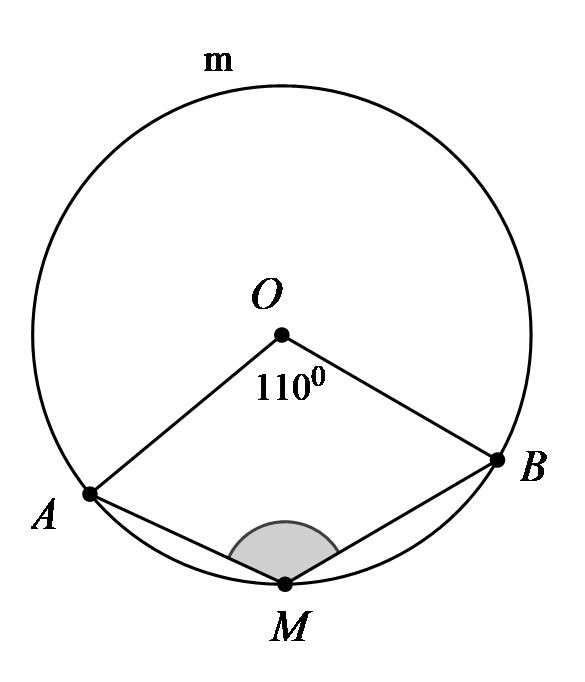
Bài toán 4. Tính số đo ![]() trong mối trường hợp ở hình.
trong mối trường hợp ở hình.

Bài toán 5. ![]() và
và ![]() là hai đường kính vuông góc của đường tròn
là hai đường kính vuông góc của đường tròn ![]() . Kẻ dây
. Kẻ dây ![]() qua trung điểm
qua trung điểm ![]() của
của ![]() .
. ![]() cắt
cắt ![]() ở
ở ![]() .
.
a) Tính độ dài ![]() .
.
b) Kẻ đường cao ![]() của tam giác
của tam giác ![]() . Tính diện tích tam giác
. Tính diện tích tam giác ![]() .
.
Bài toán 6. Cho ![]() nội tiếp trong đường tròn
nội tiếp trong đường tròn ![]() . Tia phân giác của góc
. Tia phân giác của góc ![]() cǎ́t
cǎ́t ![]() ở
ở ![]() và cắt đường tròn ở
và cắt đường tròn ở ![]() . Chứng minh rằng:
. Chứng minh rằng:
a) ![]() ; b)
; b) ![]() .
.
Bài toán 7. Từ điểm ![]() nằm ngoài đường tròn
nằm ngoài đường tròn ![]() , kẻ cát tuyến
, kẻ cát tuyến ![]() . Gọi
. Gọi ![]() là điểm chính giữa của cung
là điểm chính giữa của cung ![]() . Kẻ đường kính
. Kẻ đường kính ![]() cắt
cắt ![]() tại
tại ![]() , ID cắt
, ID cắt ![]() tại
tại ![]() . Chứng minh rằng:
. Chứng minh rằng: ![]() .
.
Bài toán 9. Đỉnh ![]() của tam giác
của tam giác ![]() với các góc nhọn được nối với tâm
với các góc nhọn được nối với tâm ![]() của đường tròn ngoại tiếp. Từ
của đường tròn ngoại tiếp. Từ ![]() vẽ đường cao
vẽ đường cao ![]() . Chứng minh ràng
. Chứng minh ràng ![]() .
.
Bài toán 10. Cho tam giác ![]() cân tại
cân tại ![]() nội tiếp trong đường tròn
nội tiếp trong đường tròn ![]() , qua
, qua ![]() kẻ đường thẳng cắt cạnh
kẻ đường thẳng cắt cạnh ![]() tại
tại ![]() và cắt
và cắt ![]() tại
tại ![]() .
.
a) Chứng minh rằng ![]() .
.
b) Chứng tỏ tích ![]() không đổi (không phụ thuộc vào vị trí điểm
không đổi (không phụ thuộc vào vị trí điểm ![]() ) hãy tính tích
) hãy tính tích ![]() theo
theo ![]() và đường cao
và đường cao ![]() của tam giác kẻ từ
của tam giác kẻ từ ![]() .
.
Bài toán 11. Từ một điểm ![]() nằm ngoài đường tròn
nằm ngoài đường tròn ![]() , kẻ hai tiếp tuyến
, kẻ hai tiếp tuyến ![]() đến
đến ![]() , là hai tiếp điểm). Trên dây
, là hai tiếp điểm). Trên dây ![]() lấy
lấy ![]() bất kì. Qua
bất kì. Qua ![]() kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với ![]() cắt
cắt ![]() tại
tại ![]() và
và ![]() tại
tại ![]() . Chứng minh rằng:
. Chứng minh rằng: ![]() .
.
Bài toán 12. Cho tam giác đều ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]() . Một điểm
. Một điểm ![]() nằm trên cung nhỏ
nằm trên cung nhỏ ![]() . Trên đoạn
. Trên đoạn ![]() lấy
lấy ![]() .
.
a) Chứng tỏ rằng ![]() đều.
đều.
b) Chứng tỏ rằng: ![]() .
.
📥 Để xem trọn vẹn nội dung và ví dụ minh họa, bạn vui lòng tải tài liệu tham khảo tại đây.
-----------------------------------
Hy vọng rằng chuyên đề góc nội tiếp Toán 9 đã giúp bạn nắm vững kiến thức lý thuyết, rèn luyện kỹ năng giải bài tập và tự tin hơn khi bước vào các kỳ thi. Đừng quên luyện tập thường xuyên và tham khảo thêm các chuyên đề Toán lớp 9 khác trên website để học tốt môn Toán một cách toàn diện. Chúc bạn học tập hiệu quả và đạt kết quả cao!










