Tìm tham số m để phương trình có n nghiệm (dựa vào đồ thị hàm số)
Tìm m để phương trình có nghiệm - Có đáp án
Trong chương trình Toán 12, dạng bài tìm tham số m để phương trình có n nghiệm là một trong những chuyên đề quan trọng thuộc bài toán tương giao đồ thị hàm số. Đây là dạng bài thường gặp trong đề thi THPT Quốc gia, yêu cầu học sinh nắm vững kiến thức về đồ thị hàm số, tính đơn điệu và số nghiệm phương trình. Bài viết này sẽ giúp bạn hiểu bản chất bài toán, cách giải nhanh và chính xác, đồng thời có ví dụ minh họa chi tiết kèm đáp án, giúp bạn tự tin chinh phục mọi dạng bài tương tự.
A. Ví dụ minh họa tìm m để phương trình có nghiệm
Ví dụ 1. Cho hàm số ![]() \(f(x) = x^{3} - 3x^{2}
+ 2\) có đồ thị là đường cong trong hình bên:
\(f(x) = x^{3} - 3x^{2}
+ 2\) có đồ thị là đường cong trong hình bên:
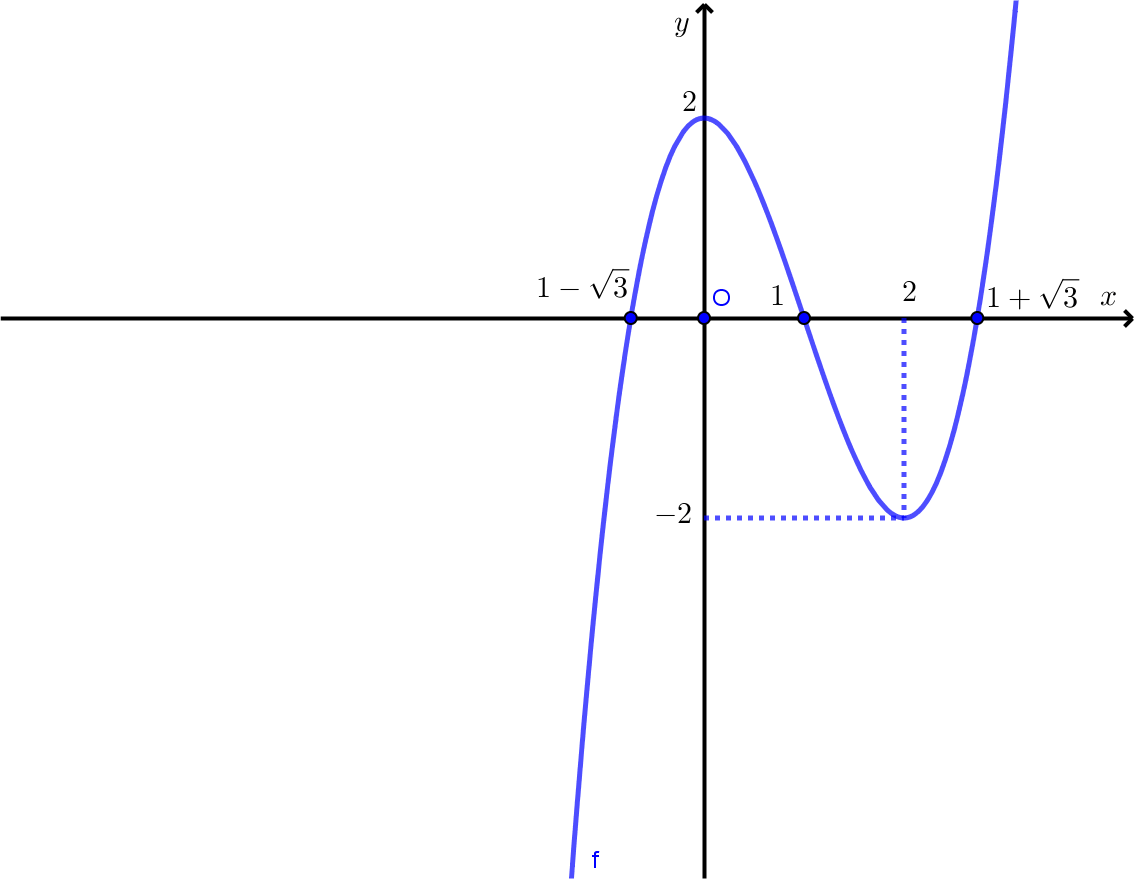
Hỏi phương trình ![]() \(\left( x^{3} - 3x^{2} +
2 \right)^{3} - 3\left( x^{3} - 3x^{2} + 2 \right)^{2} + 2 = 0\) có bao nhiêu nghiệm thực dương phân biệt?
\(\left( x^{3} - 3x^{2} +
2 \right)^{3} - 3\left( x^{3} - 3x^{2} + 2 \right)^{2} + 2 = 0\) có bao nhiêu nghiệm thực dương phân biệt?
A. ![]() \(3\). B.
\(3\). B. ![]() \(5\). C.
\(5\). C. ![]() \(7\). D.
\(7\). D. ![]() \(1\).
\(1\).
Hướng dẫn giải
Chọn B.
Đặt ![]() \(t = x^{3} - 3x^{2} + 2\), ta có phương trình
\(t = x^{3} - 3x^{2} + 2\), ta có phương trình  \(t^{3} - 3t^{2} + 2 = 0
\Leftrightarrow \left\lbrack \begin{matrix}
t = 1 \\
t = 1 + \sqrt{3} \\
t = 1 - \sqrt{3}
\end{matrix} \right.\).
\(t^{3} - 3t^{2} + 2 = 0
\Leftrightarrow \left\lbrack \begin{matrix}
t = 1 \\
t = 1 + \sqrt{3} \\
t = 1 - \sqrt{3}
\end{matrix} \right.\).
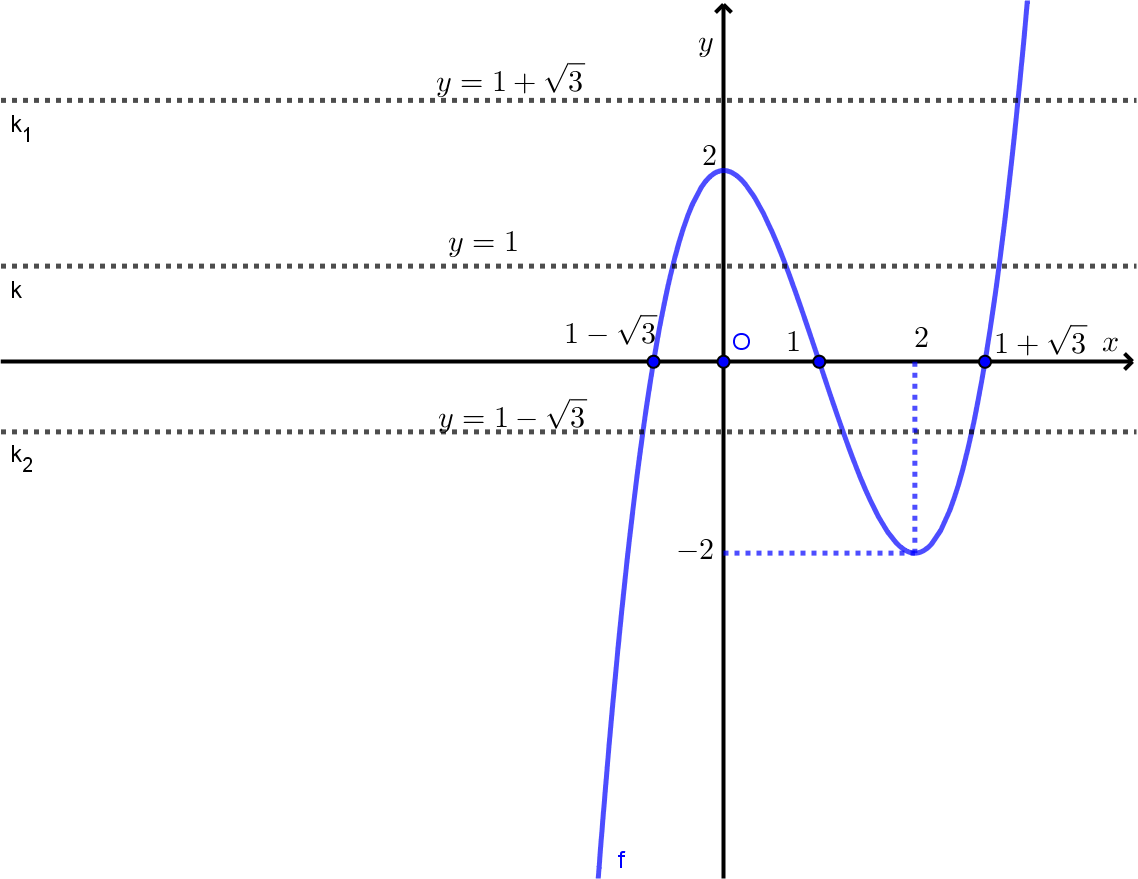
Với ![]() \(t = 1 \Rightarrow f(x) = 1\). Quan sát đồ thị hàm số
\(t = 1 \Rightarrow f(x) = 1\). Quan sát đồ thị hàm số ![]() \(y = f(x)\), ta thấy đường thẳng
\(y = f(x)\), ta thấy đường thẳng ![]() \(y = 1\) cắt đồ thị hàm số
\(y = 1\) cắt đồ thị hàm số ![]() \(y = f(x)\) tại
\(y = f(x)\) tại ![]() \(3\) điểm phân biệt trong đó có hai điểm có hoành độ dương nên phương trình
\(3\) điểm phân biệt trong đó có hai điểm có hoành độ dương nên phương trình ![]() \(t =
1\) có hai nghiệm
\(t =
1\) có hai nghiệm ![]() \(x\) dương phân biệt.
\(x\) dương phân biệt.
Với ![]() \(t = 1 + \sqrt{3}\). Quan sát đồ thị hàm số
\(t = 1 + \sqrt{3}\). Quan sát đồ thị hàm số ![]() \(y = f(x)\), ta thấy đường thẳng
\(y = f(x)\), ta thấy đường thẳng ![]() \(y = 1 + \sqrt{3}\) cắt đồ thị hàm số
\(y = 1 + \sqrt{3}\) cắt đồ thị hàm số ![]() \(y = f(x)\)tại một điểm và là điểm có hoành độ dương nên phương trình
\(y = f(x)\)tại một điểm và là điểm có hoành độ dương nên phương trình ![]() \(t
= 1 + \sqrt{3}\) có một nghiệm
\(t
= 1 + \sqrt{3}\) có một nghiệm ![]() \(x\) dương.
\(x\) dương.
Với ![]() \(t = 1 - \sqrt{3}\). Quan sát đồ thị hàm số
\(t = 1 - \sqrt{3}\). Quan sát đồ thị hàm số ![]() \(y = f(x)\), ta thấy đường thẳng
\(y = f(x)\), ta thấy đường thẳng ![]() \(y = 1 - \sqrt{3}\) cắt đồ thị hàm số
\(y = 1 - \sqrt{3}\) cắt đồ thị hàm số ![]() \(y = f(x)\) tại
\(y = f(x)\) tại ![]() \(3\) điểm phân biệt trong đó có hai điểm có hoành độ dương nên phương trình
\(3\) điểm phân biệt trong đó có hai điểm có hoành độ dương nên phương trình ![]() \(t = 1 -
\sqrt{3}\) có hai nghiệm
\(t = 1 -
\sqrt{3}\) có hai nghiệm ![]() \(x\) dương phân biệt.
\(x\) dương phân biệt.
Vậy phương trình bài ra có ![]() \(5\) nghiệm phân biệt dương.
\(5\) nghiệm phân biệt dương.
Ví dụ 2. Cho hàm số ![]() \(y = f(x)\) liên tục trên
\(y = f(x)\) liên tục trên ![]() \(\mathbb{R}\) và có đồ thị như hình vẽ:
\(\mathbb{R}\) và có đồ thị như hình vẽ:
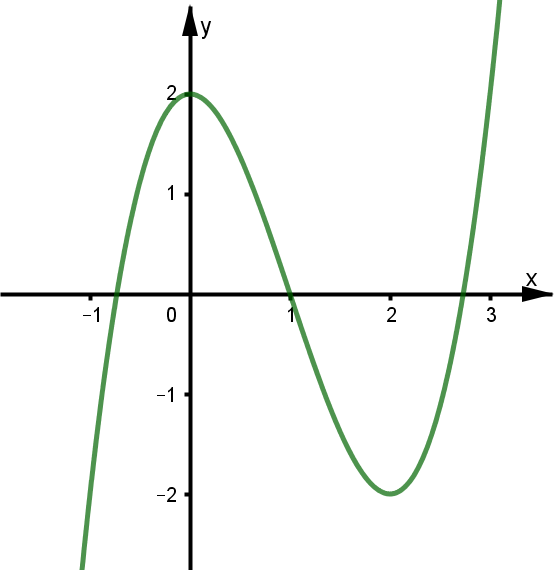
Gọi ![]() \(m\) là số nghiệm của phương trình
\(m\) là số nghiệm của phương trình ![]() \(f\left( f(x) \right) = 1\). Khẳng định nào sau đây là đúng?
\(f\left( f(x) \right) = 1\). Khẳng định nào sau đây là đúng?
A. ![]() \(m = 6\). B.
\(m = 6\). B. ![]() \(m = 7\). C.
\(m = 7\). C. ![]() \(m =
5\). D.
\(m =
5\). D. ![]() \(m = 9\).
\(m = 9\).
Hướng dẫn giải
Chọn B
Đặt ![]() \(f(x) = u\) khi đó nghiệm của phương trình
\(f(x) = u\) khi đó nghiệm của phương trình ![]() \(f\left( f(x) \right) =
1\) chính là hoành độ giao điểm của đồ thị
\(f\left( f(x) \right) =
1\) chính là hoành độ giao điểm của đồ thị ![]() \(f(u)\) với đường thẳng
\(f(u)\) với đường thẳng ![]() \(y = 1\).
\(y = 1\).
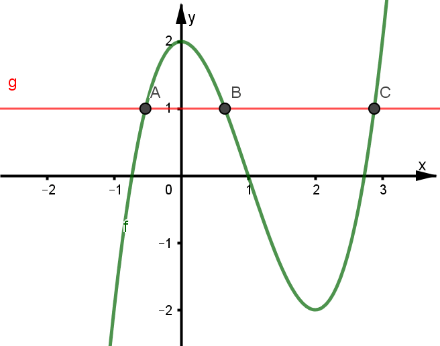
Dựa vào đồ thị ta có ba nghiệm  \(\left\lbrack \begin{matrix}
f(x) = u_{1} \\
f(x) = u_{2} \\
f(x) = u_{3}
\end{matrix} \right.\) với
\(\left\lbrack \begin{matrix}
f(x) = u_{1} \\
f(x) = u_{2} \\
f(x) = u_{3}
\end{matrix} \right.\) với ![]() \(u_{1}
\in ( - 1;0)\),
\(u_{1}
\in ( - 1;0)\), ![]() \(u_{2} \in
(0;1)\),
\(u_{2} \in
(0;1)\),![]() \(u_{3} \in \left(
\frac{5}{2};3 \right)\).
\(u_{3} \in \left(
\frac{5}{2};3 \right)\).
Tiếp tục xét số giao điểm của đồ thị hàm số ![]() \(f(x)\) với từng đường thẳng
\(f(x)\) với từng đường thẳng ![]() \(y = u_{1}\),
\(y = u_{1}\), ![]() \(y
= u_{2}\),
\(y
= u_{2}\), ![]() \(y = u_{3}\).
\(y = u_{3}\).
Dựa vào đồ thị ta có được ![]() \(7\) giao điểm. Suy ra phương trình ban đầu
\(7\) giao điểm. Suy ra phương trình ban đầu ![]() \(f\left(
f(x) \right) = 1\) có
\(f\left(
f(x) \right) = 1\) có ![]() \(7\) nghiệm.
\(7\) nghiệm.
Ví dụ 3. Cho hàm số ![]() \(f(x)\) có đồ thị là đường cong như hình vẽ bên dưới:
\(f(x)\) có đồ thị là đường cong như hình vẽ bên dưới:
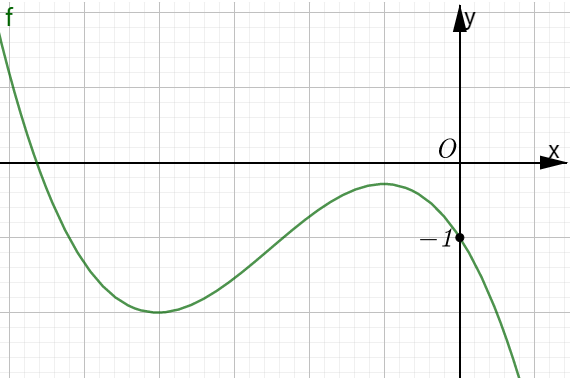
Số nghiệm thực phân biệt của phương trình ![]() \(f\left( x^{3}f(x) \right) + 1 = 0\) là:
\(f\left( x^{3}f(x) \right) + 1 = 0\) là:
A. ![]() \(6\). B.
\(6\). B. ![]() \(4\). C.
\(4\). C. ![]() \(5\). D.
\(5\). D. ![]() \(8\).
\(8\).
Hướng dẫn giải
Chọn A
Dựa vào đồ thị, ta thấy ![]() \(f\left( x^{3}f(x)
\right) + 1 = 0 \Leftrightarrow f\left( x^{3}f(x) \right) = -
1\)
\(f\left( x^{3}f(x)
\right) + 1 = 0 \Leftrightarrow f\left( x^{3}f(x) \right) = -
1\)
 \(\Leftrightarrow \left\lbrack
\begin{matrix}
x^{3}f(x) = a \in ( - 6; - 5)\ \ \ (1) \\
x^{3}f(x) = b \in ( - 3; - 2)\ \ \ (2) \\
x^{3}f(x) = 0\ \ \ (3)
\end{matrix} \right.\)
\(\Leftrightarrow \left\lbrack
\begin{matrix}
x^{3}f(x) = a \in ( - 6; - 5)\ \ \ (1) \\
x^{3}f(x) = b \in ( - 3; - 2)\ \ \ (2) \\
x^{3}f(x) = 0\ \ \ (3)
\end{matrix} \right.\)
+ Phương trình ![]() \((3)\) tương đương
\((3)\) tương đương ![]() \(\left\lbrack \begin{matrix}
x = 0 \\
f(x) = 0
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
x = 0 \\
x = x_{1},\ \ \ \left( - 6 < x_{1} < a < - 5 \right)
\end{matrix} \right.\).
\(\left\lbrack \begin{matrix}
x = 0 \\
f(x) = 0
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
x = 0 \\
x = x_{1},\ \ \ \left( - 6 < x_{1} < a < - 5 \right)
\end{matrix} \right.\).
+ Các hàm số ![]() \(g(x) =
\frac{a}{x^{3}}\) và
\(g(x) =
\frac{a}{x^{3}}\) và ![]() \(h(x) =
\frac{b}{x^{3}}\) đồng biến trên các khoảng
\(h(x) =
\frac{b}{x^{3}}\) đồng biến trên các khoảng ![]() \(( - \infty;0)\) và
\(( - \infty;0)\) và ![]() \((0; + \infty)\), và nhận xét rằng
\((0; + \infty)\), và nhận xét rằng ![]() \(x = 0\) không phải là nghiệm của phương trình
\(x = 0\) không phải là nghiệm của phương trình ![]() \((1)\) nên:
\((1)\) nên:
![]() \((1) \Leftrightarrow \left\lbrack
\begin{matrix}
f(x) = g(x) \\
f(x) = h(x)
\end{matrix} \right.\).
\((1) \Leftrightarrow \left\lbrack
\begin{matrix}
f(x) = g(x) \\
f(x) = h(x)
\end{matrix} \right.\).
+ Trên khoảng ![]() \(( - \infty;0)\), ta có
\(( - \infty;0)\), ta có  \(\left\{ \begin{matrix}
\lim_{x \rightarrow - \infty}f(x) = + \infty;\ \ \ \lim_{x \rightarrow
0^{-}}f(x) = - 1 \\
\lim_{x \rightarrow - \infty}g(x) = \lim_{x \rightarrow - \infty}h(x) =
0 \\
\lim_{x \rightarrow 0^{-}}g(x) = \lim_{x \rightarrow 0^{-}}h(x) = +
\infty
\end{matrix} \right.\) nên các phương trình
\(\left\{ \begin{matrix}
\lim_{x \rightarrow - \infty}f(x) = + \infty;\ \ \ \lim_{x \rightarrow
0^{-}}f(x) = - 1 \\
\lim_{x \rightarrow - \infty}g(x) = \lim_{x \rightarrow - \infty}h(x) =
0 \\
\lim_{x \rightarrow 0^{-}}g(x) = \lim_{x \rightarrow 0^{-}}h(x) = +
\infty
\end{matrix} \right.\) nên các phương trình ![]() \(f(x) = g(x)\) và
\(f(x) = g(x)\) và ![]() \(f(x) = h(x)\) có nghiệm duy nhất.
\(f(x) = h(x)\) có nghiệm duy nhất.
+ Trên khoảng ![]() \((0; + \infty)\), ta có
\((0; + \infty)\), ta có  \(\left\{ \begin{matrix}
\lim_{x \rightarrow + \infty}f(x) = - \infty;\ \ \ \lim_{x \rightarrow
0^{+}}f(x) = - 1 \\
\lim_{x \rightarrow + \infty}g(x) = \lim_{x \rightarrow + \infty}h(x) =
0 \\
\lim_{x \rightarrow 0^{+}}g(x) = \lim_{x \rightarrow 0^{+}}h(x) = -
\infty
\end{matrix} \right.\) nên các phương trình
\(\left\{ \begin{matrix}
\lim_{x \rightarrow + \infty}f(x) = - \infty;\ \ \ \lim_{x \rightarrow
0^{+}}f(x) = - 1 \\
\lim_{x \rightarrow + \infty}g(x) = \lim_{x \rightarrow + \infty}h(x) =
0 \\
\lim_{x \rightarrow 0^{+}}g(x) = \lim_{x \rightarrow 0^{+}}h(x) = -
\infty
\end{matrix} \right.\) nên các phương trình ![]() \(f(x) = g(x)\) và
\(f(x) = g(x)\) và ![]() \(f(x) = h(x)\) có nghiệm duy nhất.
\(f(x) = h(x)\) có nghiệm duy nhất.
Do đó, phương trình ![]() \(f\left( x^{3}f(x)
\right) + 1 = 0\) có
\(f\left( x^{3}f(x)
\right) + 1 = 0\) có ![]() \(6\) nghiệm phân biệt.
\(6\) nghiệm phân biệt.
B. Bài tập tự rèn luyện tìm m để phương trình có n nghiệm có đáp án cụ thể
Bài tập 1. Cho hàm số bậc ba ![]() \(y =
f(x)\) có đồ thị là đường cong trong hình vẽ bên:
\(y =
f(x)\) có đồ thị là đường cong trong hình vẽ bên:
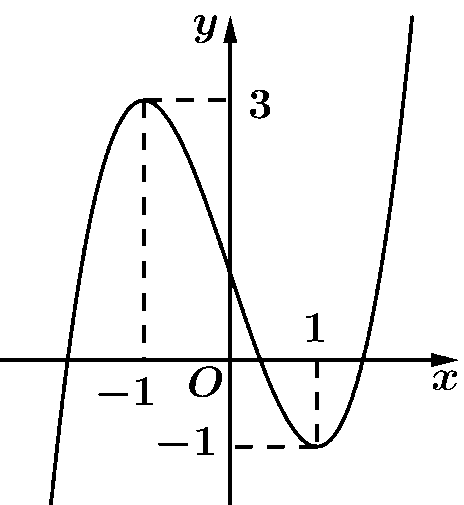
Số nghiệm thực của phương trình ![]() \(f(x) =
2\) là:
\(f(x) =
2\) là:
A. ![]() \(0\). B.
\(0\). B. ![]() \(3\). C.
\(3\). C. ![]() \(1\). D.
\(1\). D. ![]() \(2\).
\(2\).
Bài tập 2. Cho hàm số ![]() \(f(x) = ax^{3} +
bx^{2} + cx + d\) có đồ thị như hình vẽ dưới đây:
\(f(x) = ax^{3} +
bx^{2} + cx + d\) có đồ thị như hình vẽ dưới đây:
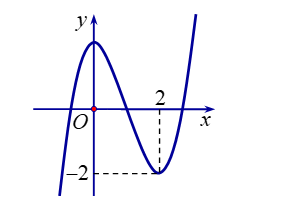
Số nghiệm của phương trình ![]() \(f(x) + 1 =
0\) là:
\(f(x) + 1 =
0\) là:
A. ![]() \(2\). B.
\(2\). B. ![]() \(3\). C.
\(3\). C. ![]() \(0\). D.
\(0\). D. ![]() \(1\).
\(1\).
Bài tập 3. Cho hàm số ![]() \(y = f(x)\) liên tục trên
\(y = f(x)\) liên tục trên ![]() \(\mathbb{R}\) và có đồ thị ở hình bên.
\(\mathbb{R}\) và có đồ thị ở hình bên.
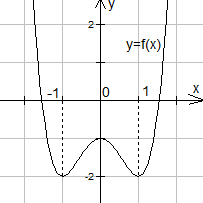
Số nghiệm dương phân biệt của phương trình ![]() \(f(x) = - \sqrt{3}\) là
\(f(x) = - \sqrt{3}\) là
A. ![]() \(1\). B.
\(1\). B. ![]() \(3\). C.
\(3\). C. ![]() \(2\). D.
\(2\). D. ![]() \(4\).
\(4\).
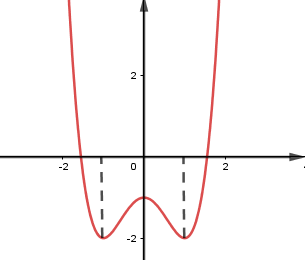
Bài tập 4. Cho hàm số ![]() \(y = f(x)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình
\(y = f(x)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình ![]() \(f(x) + 1 = 0\) là:
\(f(x) + 1 = 0\) là:
A. ![]() \(1\). B.
\(1\). B. ![]() \(3\). C.
\(3\). C. ![]() \(4\) D.
\(4\) D. ![]() \(2\).
\(2\).
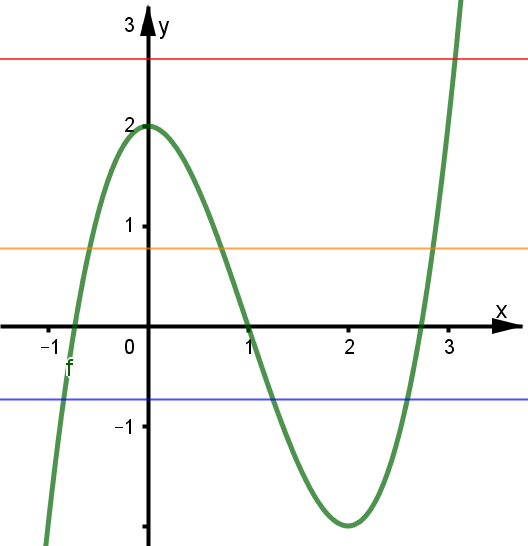
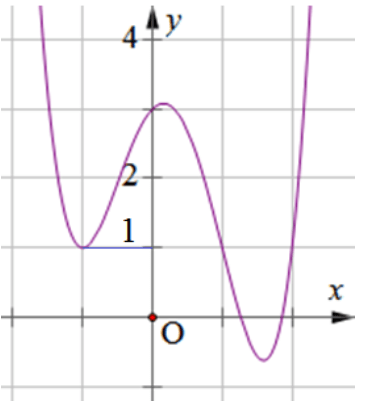
Bài tập 5. Cho hàm số ![]() \(y = f(x)\) có đồ thị như đường cong hình dưới. Phương trình
\(y = f(x)\) có đồ thị như đường cong hình dưới. Phương trình ![]() \(f(x) = 1\) có bao nhiêu nghiệm?
\(f(x) = 1\) có bao nhiêu nghiệm?
A. ![]() \(2\). B.
\(2\). B. ![]() \(4\). C.
\(4\). C. ![]() \(1\). D.
\(1\). D. ![]() \(3\).
\(3\).
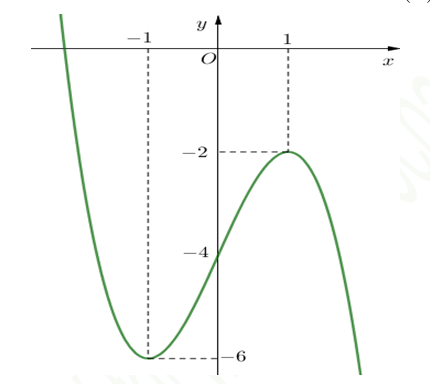
Bài tập 6. Cho hàm số ![]() \(y = f(x)\) có đồ thị như hình vẽ bên. Phương trình
\(y = f(x)\) có đồ thị như hình vẽ bên. Phương trình ![]() \(f(x)
= - 3\) có số nghiệm là:
\(f(x)
= - 3\) có số nghiệm là:
A. ![]() \(0\). B.
\(0\). B. ![]() \(1\). C.
\(1\). C. ![]() \(2\). D.
\(2\). D. ![]() \(3\).
\(3\).
Bài tập 7. Cho hàm số ![]() \(y = f(x)\) có đồ thi
\(y = f(x)\) có đồ thi ![]() \((C)\)như hình vẽ:
\((C)\)như hình vẽ:
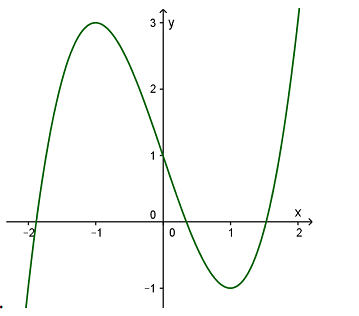
Số nghiệm phân biệt của phương trình ![]() \(f(x)
= \frac{1}{2}\) là :
\(f(x)
= \frac{1}{2}\) là :
A. ![]() \(2\). B.
\(2\). B. ![]() \(3\). C.
\(3\). C. ![]() \(0\). D.
\(0\). D. ![]() \(1\).
\(1\).
Bài tập 8. Cho hàm số ![]() \(y = f(x)\) có đồ thị như hình bên dưới:
\(y = f(x)\) có đồ thị như hình bên dưới:
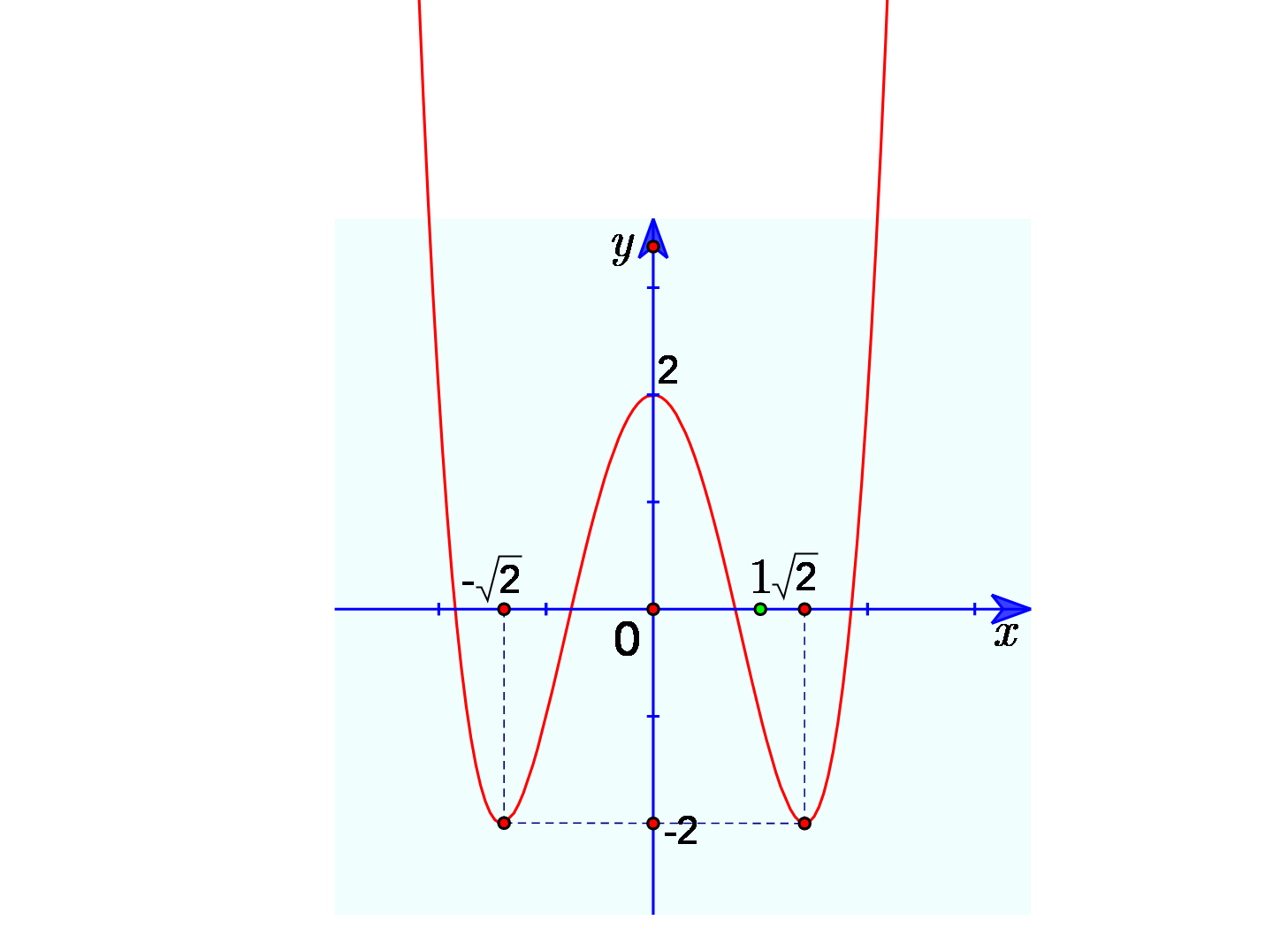
Số nghiệm của phương trình ![]() \(2f(x) + 3 =
0\) là:
\(2f(x) + 3 =
0\) là:
A. ![]() \(4\). B.
\(4\). B. ![]() \(2\). C.
\(2\). C. ![]() \(0\). D.
\(0\). D. ![]() \(3\).
\(3\).
Bài tập 9. Cho hàm số ![]() \(y = f(x)\) có đồ thị trong hình bên. Phương trình
\(y = f(x)\) có đồ thị trong hình bên. Phương trình ![]() \(f(x)
= 1\) có bao nhiêu nghiệm thực phân biệt lớn hơn
\(f(x)
= 1\) có bao nhiêu nghiệm thực phân biệt lớn hơn ![]() \(2\).
\(2\).
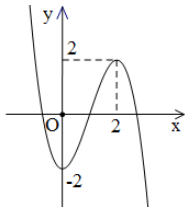
A. ![]() \(0\). B.
\(0\). B. ![]() \(1\). C.
\(1\). C. ![]() \(2\). D.
\(2\). D. ![]() \(3\).
\(3\).
Bài tập 10. Cho hàm số ![]() \(y = ax^{4} +
bx^{2} + c\) có đồ thị như hình vẽ bên:
\(y = ax^{4} +
bx^{2} + c\) có đồ thị như hình vẽ bên:
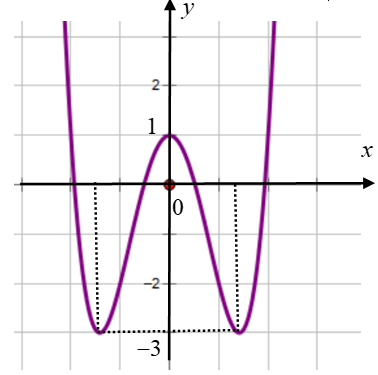
Số nghiệm của phương trình ![]() \(f(x) + 3 =
0\) là:
\(f(x) + 3 =
0\) là:
A. ![]() \(4\). B.
\(4\). B. ![]() \(3\). C.
\(3\). C. ![]() \(1\). D.
\(1\). D. ![]() \(2\).
\(2\).
Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.
-------------------------------------------------------
Bài toán tìm tham số m để phương trình có n nghiệm dựa vào đồ thị hàm số không chỉ rèn luyện kỹ năng phân tích mà còn giúp bạn hiểu sâu hơn về mối quan hệ giữa hàm số và phương trình. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trong bài, bạn có thể nhận diện nhanh dạng bài, lập luận chính xác và tối ưu thời gian làm bài thi.
👉 Đừng quên ôn tập thêm các chuyên đề đồ thị hàm số Toán 12 khác để nắm chắc điểm 9-10 trong kỳ thi sắp tới!










