Toán lớp 6 Bài 1: Phân số với tử và mẫu là số nguyên Cánh Diều

Toán lớp 6 Bài 1: Phân số với tử và mẫu là số nguyên sách Cánh Diều Có đáp án chi tiết cho từng bài tập, giúp các em học sinh củng cố, hệ thống lại toàn bộ bài học, kỹ năng giải Toán.

I. Khái niệm phân số

Hoạt động 1 trang 25 Toán 6 Tập 2 Cánh diều

Một tòa nhà chung cư có ba tầng hầm được kí hiệu theo thứ tự từ trên xuống là B1, B2, B3. Độ cao của ba tầng hầm là bằng nhau. Biết rằng độ cao của mặt sàn tầng hầm B3 so với mặt đất là -10 m. Tính độ cao của mặt sàn tầng hầm B1 so với mặt đất.

Đáp án

Độ cao của mặt sàn tầng hầm B1 so với mặt đất là:

-10:3 = $\frac{-10}{3}$ (m)

Hoạt động 2 trang 25 Toán lớp 6 Tập 2:

Viết kết quả của phép chia a : b trong mỗi trường hợp sau theo mẫu:

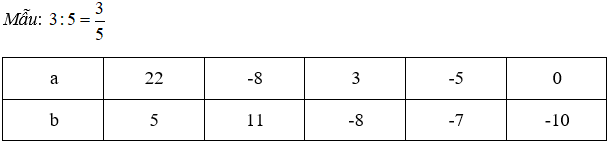
Lời giải chi tiết

$22:5=\frac{22}{5};$

$-8:11=\frac{-8}{11};$

$3:(-8)=\frac{3}{-8};$

$(-5):(-7)=\frac{-5}{-7};$

$0:(-10)=\frac{0}{-10}$

Luyện tập 1 trang 26 Toán lớp 6 Tập 2:

Viết và đọc phân số trong mỗi trường hợp sau:

a) Tử số là - 6, mẫu số là 17;

b) Tử số là - 12, mẫu số là -37.

Hướng dẫn giải:

a) Phân số có tử số là – 6 và mẫu số là 17, được viết là:

Đọc là âm sáu phần mười bảy.

b) Phân số có tử số là -12 và mẫu số là – 37, được viết là:

Đọc là âm mười hai phần âm ba mươi bảy.

II. Phân số bằng nhau

Hoạt động 3 trang 26 Toán lớp 6 Tập 2:

a) Viết các phân số biểu thị phần đã tô màu trong mỗi hình bên.

b) Hai phân số đó có bằng nhau không?

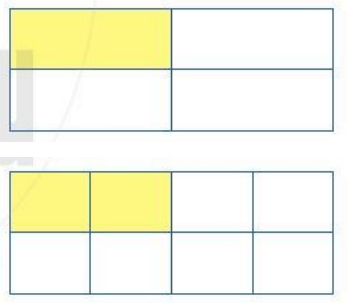
Hướng dẫn giải:

Ta xét hình:

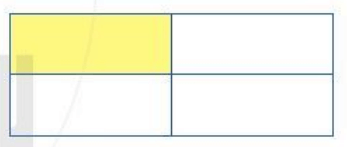
Ở hình này ta thấy cả hình chữ nhật được chia làm 4 phần, phần tô màu chiếm 1 phần. Do đó phân số biểu thị cho phần đã tô màu là: .

Ta xét hình:

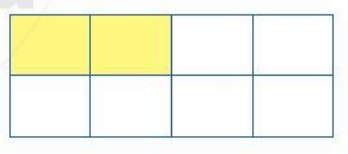
Ở hình này ta thấy cả hình chữ nhật được chia làm 8 phần, phần tô màu chiếm 2 phần. Do đó phân số biểu thị cho phần đã tô màu là: .

b) Hình chữ nhật bên ngoài của cả hai hình đều bằng nhau hơn nữa phần tô màu của hai hình cũng bằng nhau nên hai phân số biểu thị bằng nhau, ta viết: .

Hoạt động 4 trang 26 Toán lớp 6 Tập 2:

Xét hai phân số bằng nhau . So sánh tích của tử ở phân số thứ nhất và mẫu ở phân số thứ hai với tích của mẫu ở phân số thứ nhất và tử ở phân số thứ hai.

Hướng dẫn giải:

Tích của tử ở phân số thứ nhất và mẫu ở phân số thứ hai là: 1.8 = 8.

Tích của tử ở phân số thứ hai và mẫu ở phân số thứ nhất là: 2.4 = 8.

Do đó: 1.8 = 2.4.

Vậy tích của tử ở phân số thứ nhất và mẫu ở phân số thứ hai bằng tích của mẫu ở phân số thứ nhất và tử ở phân số thứ hai.

III. Tính chất cơ bản của phân số

Hoạt động 5 trang 27 Toán lớp 6 Tập 2:

Ta có: vì 1.10= 5.2 (quy tắc bằng nhau của hai phân số).

Tìm số nguyên thích hợp ở :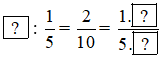

b) Ta có: vì 4. (- 6) = 24. (-1) (quy tắc bằng nhau của bai phân số).

Tìm số nguyên thích hợp ở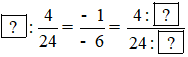

Hướng dẫn giải:

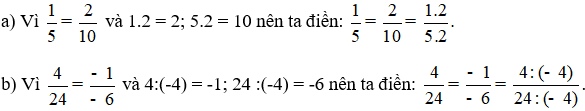
Hoạt động 6 trang 28 Toán lớp 6 Tập 2:

Nêu cách rút gọn phân số với tử và mẫu là số nguyên dương về phân số tối giản.

Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là 1 và - 1.

Đáp án

Cách rút gọn phân số với tử và mẫu là số nguyên dương về phân số tối giản:

Dựa vào tính chất cơ bản của phân số, để rút gọn phân số với tử và mẫu là số nguyên về phân số tối giản ta thường làm như sau:

Bước 1. Tìm ƯCLN của tử và mẫu sau khi đã bỏ đi dấu "-” (nếu có)

Bước 2. Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản cần tìm.

Hoạt động 7 trang 29 Toán lớp 6 Tập 2:

Nêu cách quy đồng mẫu nhiều phân số có tử và mẫu là số nguyên dương.

Đáp án

Dựa vào tính chất cơ bản của phân số ta có thể quy đồng mẫu nhiều phân số có tử và mẫu là số nguyên.

Để quy đồng mẫu nhiều phân số, ta thường làm như sau:

Bước 1. Viết các phân số đã cho về phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu chung.

Bước 2. Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3. Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.

Bài tập

Bài 1 trang 30 Toán lớp 6 Tập 2

Viết và đọc phân số trong mỗi trường hợp sau:

a) Tử số là - 43, mẫu số là 19;

b) Tử số là - 123, mẫu số là - 63.

Đáp án

a) Phân số có tử số là - 43, mẫu số

Viết là: $\frac{-43}{19}$

Đọc là: âm bốn mươi ba phần mười chín.

b) Phân số có tử số là - 123, mẫu số là – 63

Viết là: $\frac{-123}{-63}$

Đọc là: âm một trăm hai mươi ba phần âm sáu mươi ba.

Bài 2 trang 30 Toán lớp 6 Tập 2

Các cặp phân số sau có bằng nhau không? Vì sao?

Đáp án

a) $\frac{-2}{9}$ và $\frac{6}{-27}$

Ta có: (-2) . (-27) = 54; 6 . 9 = 54

=> $\frac{-2}{9}=\frac{6}{-27}$

Vậy hai phân số bằng nhau.

b) $\frac{-1}{5}$ và $\frac{4}{25}$

Ta có: (-1) . 25 = -25; 4 . 5 = 20

=> (-1) . 25 ≠ 4 . 5

=> $\frac{-1}{5}\ne \frac{4}{25}$

Vậy hai phân số không bằng nhau

Bài 3 trang 30 Toán lớp 6 Tập 2

Tìm số nguyên x, biết:

Đáp án

a) $\frac{-28}{35}=\frac{16}{x}$

=> (-28) . x = 16 . 35

=> (-28) . x = 560

=> x = 560 : (-28)

=> x = -20

Vậy x = -20

b) $\frac{x+7}{15}=\frac{-24}{36}$

=> (x + 7) . 36 = 15. (-24)

=> (x + 7) . 36 = -360

=> x + 7 = (-360) : 36

=> x + 7 = -10

=> x = -10 – 7

=> x = -17

Vậy x = -17

Bài 4 trang 30 Toán lớp 6 Tập 2

Rút gọn mỗi phân số sau về phân số tối giản:

$\frac{14}{21};\frac{-36}{48};\frac{28}{-52};\frac{-54}{-90}$

Đáp án

Ta có: 14 = 2 . 7; 21 = 3 . 7

=> UCLN(14; 21) = 7

$\frac{14}{21}=\frac{14:7}{21:7}=\frac{2}{3}$

Ta có: 36 = 2².3²; 48 = 2⁴.3

=> UCLN(36; 48) = 2² . 3 = 12

$\frac{-36}{48}=\frac{\left(-36\right):12}{48:12}=\frac{-3}{4}$

Ta có: 28 = 2² . 7; 52 = 2².13

=>UCLN(28; 52) = 2² = 4

$\frac{28}{-52}=\frac{28:4}{\left(-52\right):4}=\frac{7}{-13}=\frac{7.\left(-1\right)}{\left(-13\right).\left(-1\right)}=\frac{-7}{13}$

Ta có: 54 = 2.3³; 90 = 2.3².5

=> UCLN(54; 90) = 2.3² = 18

$\frac{-54}{-90}=\frac{\left(-54\right):18}{\left(-90\right):18}=\frac{-3}{-5}=\frac{3}{5}$

Bài 5 trang 30 Toán lớp 6 Tập 2

a) Rút gọn phân số $\frac{-21}{39}$ về phân số tối giản.

b) Viết tất cả các phân số bằng $\frac{-21}{39}$ mà mẫu là số tự nhiên có hai chữ số.

Đáp án

a) Rút gọn phân số $\frac{-21}{39}$ ta có:

Ta có: 21 = 3 .7; 39 = 3 . 13

=> UCLN(21;39) = 3

$\frac{-21}{39}=\frac{\left(-21\right):3}{39:3}=\frac{-7}{13}$

b) Theo câu a ta có: $\frac{-21}{39}=\frac{-7}{13}$

Để tìm các phân số bằng với $\frac{-21}{39}$ có mẫu số là số tự nhiên có hai chữ số, ta nhân cả tử và mẫu số của phân số $\frac{-7}{13}$ với 1; 2; 3; 4; 5; 6; 7.

Ta có kết quả như sau:

$\begin{array}{c}{\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).1}{13.1}}={\displaystyle \frac{-7}{13}}\hfill \\ {\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).2}{13.2}}={\displaystyle \frac{-14}{26}}\hfill \\ {\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).3}{13.3}}={\displaystyle \frac{-21}{39}}\hfill \\ {\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).4}{13.4}}={\displaystyle \frac{-28}{52}}\hfill \\ {\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).5}{13.5}}={\displaystyle \frac{-35}{65}}\hfill \\ {\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).6}{13.6}}={\displaystyle \frac{-42}{78}}\hfill \\ {\displaystyle \frac{-7}{13}}={\displaystyle \frac{\left(-7\right).7}{13.7}}={\displaystyle \frac{-49}{91}}\hfill \end{array}$

Bài 6 trang 30 Toán lớp 6 Tập 2

Quy đồng mẫu những phân số sau:

a) $\frac{-5}{14}$ và $\frac{1}{-21}$

b) $\frac{17}{60};\frac{-5}{18};\frac{-64}{90}$ và $\frac{1}{-21}$

Đáp án

a) Thực hiện quy đồng mẫu số các phân số:

$\frac{1}{-21}=\frac{1.\left(-1\right)}{\left(-21\right).\left(-1\right)}=\frac{-1}{21}$

Ta có $\{\begin{array}{c}14=2.7\\ 21=3.7\end{array}\Rightarrow BCNN\left(14;21\right)=2.3.7=42$

Mẫu thức chung là 42

Thừa số phụ $\{\begin{array}{c}42=14.3\\ 42=21.2\end{array}$

Quy đồng phân số ta có:

$\begin{array}{c}{\displaystyle \frac{-5}{14}}={\displaystyle \frac{\left(-5\right).3}{14.3}}={\displaystyle \frac{-15}{42}}\hfill \\ {\displaystyle \frac{-1}{21}}={\displaystyle \frac{\left(-1\right).2}{21.2}}={\displaystyle \frac{-2}{41}}\hfill \end{array}$

b) Thực hiện quy đồng mẫu số các phân số:

Ta có $\{\begin{array}{c}60=2^2.3.5\\ \begin{array}{c}18={2.3}^2\\ 90={2.3}^2.5\end{array}\end{array}\Rightarrow BCNN\left(60;18;90\right)=2^2{.3}^2.5=180$

Mẫu thức chung là 180

Thừa số phụ $\{\begin{array}{c}180=60.3\\ \begin{array}{c}180=18.10\\ 180=90.2\end{array}\end{array}$

Quy đồng phân số ta có:

$\begin{array}{c}{\displaystyle \frac{17}{60}}={\displaystyle \frac{17.3}{60.3}}={\displaystyle \frac{21}{180}}\hfill \\ {\displaystyle \frac{-5}{18}}={\displaystyle \frac{\left(-5\right).10}{18.10}}={\displaystyle \frac{-50}{180}}\hfill \\ {\displaystyle \frac{-64}{90}}={\displaystyle \frac{\left(-64\right).2}{90.2}}={\displaystyle \frac{-128}{180}}\hfill \end{array}$

Bài 7 trang 30 Toán lớp 6 Tập 2

Trong các phân số sau, tìm phân số không bằng phân số nào trong các phân số còn lại:

$\frac{6}{25};\frac{-4}{50};\frac{-27}{54};\frac{-18}{-75};\frac{28}{-56}$

Đáp án

Thực hiện rút gọn phân số các phân số đã cho ta có:

$\begin{array}{c}{\displaystyle \frac{-4}{50}}={\displaystyle \frac{\left(-4\right):2}{50:2}}={\displaystyle \frac{-2}{25}}\hfill \\ {\displaystyle \frac{-27}{54}}={\displaystyle \frac{\left(-27\right):27}{54:27}}={\displaystyle \frac{-1}{2}}\hfill \\ {\displaystyle \frac{-18}{-75}}={\displaystyle \frac{\left(-18\right):\left(-3\right)}{\left(-75\right):\left(-3\right)}}={\displaystyle \frac{6}{25}}\hfill \\ {\displaystyle \frac{28}{-56}}={\displaystyle \frac{28:28}{\left(-56\right):28}}={\displaystyle \frac{1}{-2}}={\displaystyle \frac{-1}{2}}\hfill \end{array}$

Khi đó các phân số bằng nhau cần tìm là:

$\Rightarrow \{\begin{array}{c}{\displaystyle \frac{-27}{54}}={\displaystyle \frac{28}{-56}}={\displaystyle \frac{-1}{2}}\\ {\displaystyle \frac{-18}{-75}}={\displaystyle \frac{6}{25}}\end{array}$