Chuyên đề Xét tương giao dựa vào Đồ thị hàm số Toán 12 – Có đáp án chi tiết
Bài toán tương giao đồ thị hàm số có đáp án
Trong chương trình Toán 12, chuyên đề xét tương giao dựa vào đồ thị hàm số là một trong những nội dung trọng tâm, thường xuyên xuất hiện trong các đề thi THPT Quốc gia. Dạng bài này giúp học sinh rèn luyện tư duy hình học, khả năng phân tích và xác định số nghiệm phương trình thông qua đồ thị. Bài viết này sẽ cung cấp cho bạn phương pháp xét tương giao nhanh, hiệu quả, kèm đáp án chi tiết và ví dụ minh họa, giúp bạn dễ hiểu – dễ nhớ – dễ áp dụng khi làm bài thi.
A. Cách sử dụng đồ thị để xét số nghiệm phương trình
Bài toán: Xác định số nghiệm của phương trình 
\(g(x) = f(m)\ \ \ (*)\) hoặc số giao điểm giữa đường thẳng \(y = f(m)\) với đồ thị hàm số \(y = g(x)\).
Phương pháp giải:
- Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị hàm số \(y = g(x)\)và đường thẳng \(y = f(m)\)(Đường thẳng \(y = f(m)\) song song hoặc trùng với trục \(Ox\)).
- Dựa vào cực trị hoặc giá trị đặc biệt (nếu có) để xét giá trị của đường thẳng \(y = f(m)\).
B. Ví dụ minh họa xét tương giao dựa vào đồ thị hàm số
Ví dụ 1. Cho đồ thị hàm số \(y = g(x)\) như hình vẽ bên:
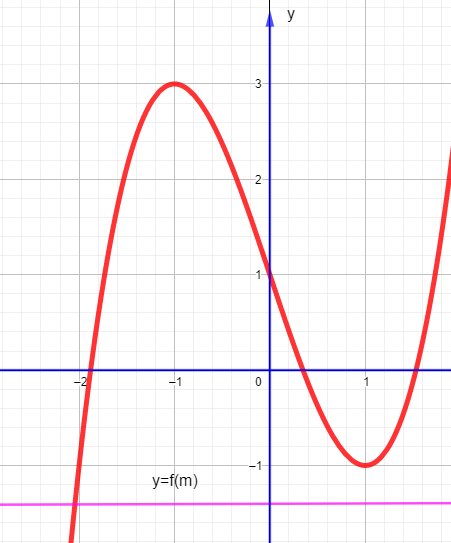
Biện luận số nghiệm của phương trình \(g(x) = f(m)\ \ \ (*)\)
Hướng dẫn giải
Dựa vào đồ thị ta có:
Phương trình (*) có \(1\) nghiệm (tức là có \(1\) giao điểm) \(\Leftrightarrow \left\lbrack \begin{matrix}
f(m) > 3 \\
f(m) < - 1
\end{matrix} \right.\) .
Phương trình (*) có \(2\) nghiệm phân biệt (tức là có \(2\) giao điểm) \(\Leftrightarrow \left\lbrack \begin{matrix}
f(m) = 3 \\
f(m) = - 1
\end{matrix} \right.\).
Phương trình (*) có \(3\) nghiệm phân biệt (tức là có \(3\) giao điểm) \(\Leftrightarrow - 1 < f(m) <
3\).
Ví dụ 2. Cho hàm số bậc ba \(y =
f(x)\) có đồ thị là đường cong trong hình bên:
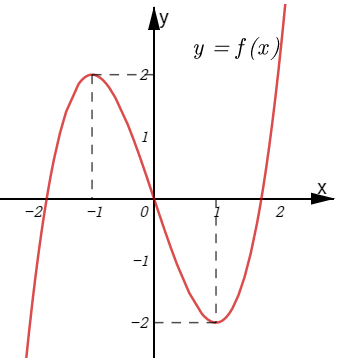
Số nghiệm thực của phương trình \(f(x) = - 1\) là:
A. \(3\). B. \(1\). C. \(0\). D. \(2\).
Hướng dẫn giải
Chọn A.
Số nghiệm thực của phương trình \(f(x) = -
1\) chính là số giao điểm của đồ thị hàm số \(y = f(x)\) và đường thẳng \(y = - 1\).
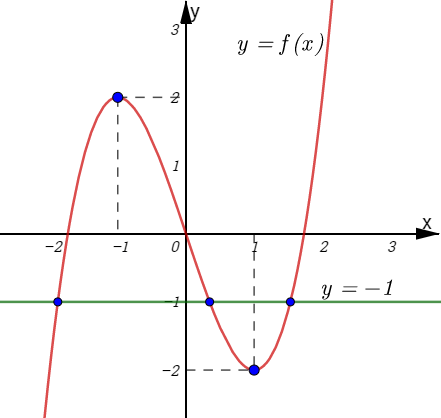
Từ hình vẽ suy ra \(3\) nghiệm.
Ví dụ 3. Cho hàm số \(y = f(x)\) có đồ thị như đường cong hình dưới:
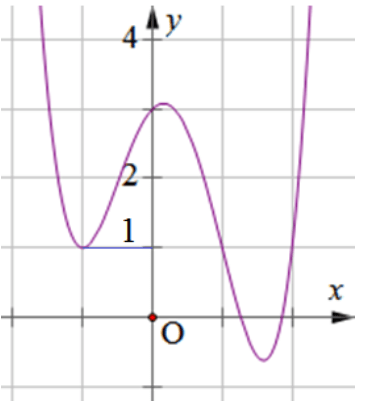
Phương trình \(f(x) = 1\) có bao nhiêu nghiệm?
A. \(2\). B. \(4\). C. \(1\). D. \(3\).
Hướng dẫn giải
Chọn D.
Số nghiệm phương trình \(f(x) = 1\) là số giao điểm của đồ thị hàm số \(1\) và đường thẳng \(y = 1\).
Dựa vào đồ thị suy ra phương trình \(f(x) =
1\) có \(3\) nghiệm phân biệt.
Ví dụ 4. Cho hàm số \(y = f(x)\) có đồ thị là đường cong trong hình vẽ bên.
Tìm số nghiệm của phương trình \(f(x + 2018) = 1\).
A. \(2\). B. \(1\). C. \(3\). D. \(4\).
Hướng dẫn giải
Chọn C
Đồ thị hàm số \(y = f(x + 2018)\) có được bằng cách tịnh tiến đồ thị hàm số \(y =
f(x)\) sang trái \(2018\) đơn vị.
Do đó số nghiệm của phương trình \(f(x +
2018) = 1\) cũng là số nghiệm của phương trình \(f(x) = 1\). Theo hình vẽ ta có số nghiệm là \(3\).
C. Bài tập tự rèn luyện xét tương giao đồ thị hàm số có đáp án chi tiết
Bài tập 1. Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ bên.
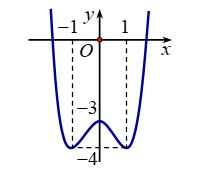
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f(x) + m - 2018 = 0\) có \(4\) nghiệm phân biệt.
A. \(2021 \leq m \leq 2022\). B. \(2021 < m < 2022\). C. \(\left\lbrack \begin{matrix}
m \geq 2022 \\
m \leq 2021
\end{matrix} \right.\). D. \(\left\lbrack \begin{matrix}
m > 2022 \\
m < 2021
\end{matrix} \right.\).
Bài tập 2. Cho đồ thị hàm số \(y =
f(x)\) có đồ thị như hình vẽ.
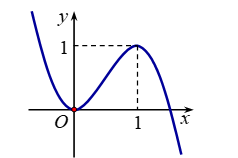
Tìm số nghiệm của phương trình \(f(x) = x\).
A. \(0\). B. \(1\). C. \(2\). D. \(3\).
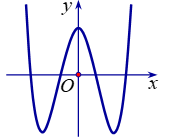
Bài tập 3. Đường cong ở hình bên là đồ thị của hàm số \(y = x^{4} + mx^{2} + n\) với \(m,n\mathbb{\in R}\). Biết phương trình \(x^{4} + mx^{2} + n = 0\) có \(k\) nghiệm thực phân biệt, \(k \in \mathbb{N}^{*}\). Mệnh đề nào dưới đây đúng?
A. \(k = 2\) và \(mn < 0\). B. \(k = 4\) và \(mn
< 0\).
C. \(k = 4\) và \(mn > 0\). D. \(k = 2\) và \(mn
> 0\).
Bài tập 4. Cho hàm số \(f(x) = x^{3} -
3x^{2} + 2\) có đồ thị là đường cong trong hình bên:
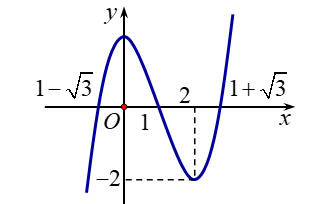
Hỏi phương trình\(\left( x^{3} - 3x^{2} + 2
\right)^{3} - 3\left( x^{3} - 3x^{2} + 2 \right)^{2} + 2 = 0\) có bao nhiêu nghiệm thực phân biệt?
A. 7. B. 9. C. 6. D. 5.
Bài tập 5. Cho hàm số bậc ba \(y =
f(x)\) có đồ thị là đường cong trong hình bên:
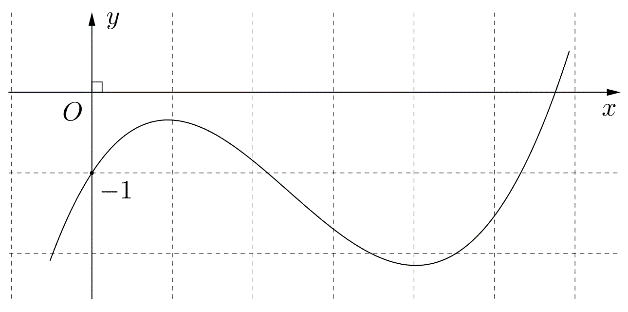
Số nghiệm thực phân biệt của phương trình \(f\left( x^{3}f(x)
\right) + 1 = 0\) là:
A. \(8\). B. \(5\). C. \(6\). D. \(4\).
Bài tập 6. Cho hàm số bậc ba \(y =
f(x)\) có đồ thị là đường cong trong hình bên:
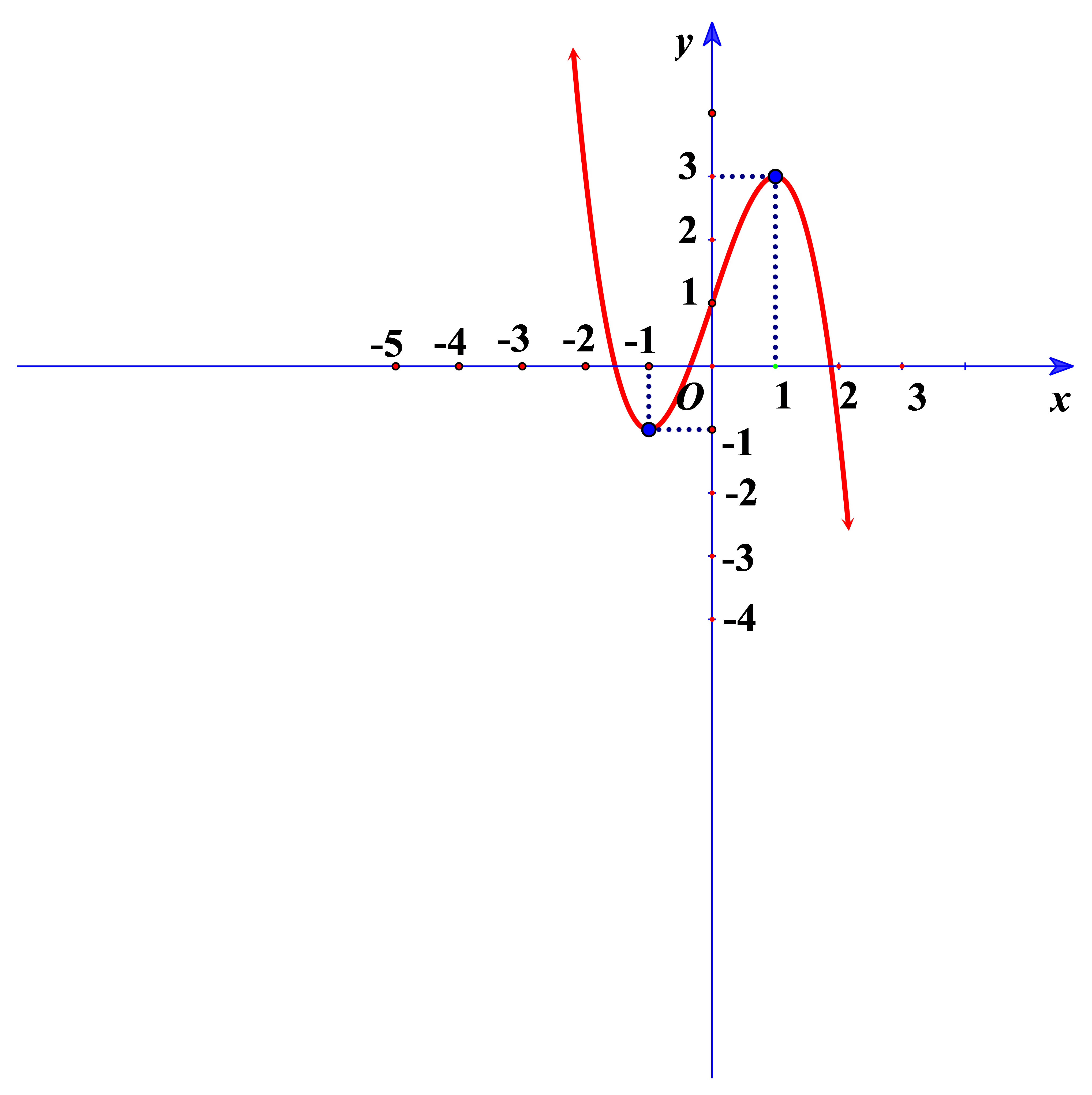
Số nghiệm thực của phương trình \(f(x) =
1\) là:
A. \(0\). B. \(3\). C. \(1\). D. \(2\).
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
------------------------------------------------------
Chuyên đề xét tương giao dựa vào đồ thị hàm số Toán 12 không chỉ giúp củng cố kiến thức về hàm số, đồ thị và phương trình, mà còn là công cụ hữu ích để giải nhanh nhiều dạng bài thi trắc nghiệm Toán. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa có đáp án, bạn sẽ nắm vững phương pháp xét tương giao, tự tin đạt điểm cao trong kỳ thi THPT Quốc gia sắp tới.
👉 Đừng quên luyện tập thêm các chuyên đề hàm số khác của Toán 12 để hoàn thiện kỹ năng giải bài nhanh và chính xác hơn!
