Phương pháp xét tương giao dựa vào đồ thị hàm trị tuyệt đối
Xét tương giao đồ thị hàm số có trị tuyệt đối
Trong chương trình Toán 12, việc xét tương giao dựa vào đồ thị hàm trị tuyệt đối là một kỹ năng quan trọng giúp học sinh hiểu sâu hơn về bản chất của đồ thị và mối quan hệ giữa các hàm số. Dạng bài này thường xuất hiện trong chuyên đề khảo sát và vẽ đồ thị hàm số, đòi hỏi khả năng tư duy hình học và đại số kết hợp. Bài viết này sẽ hướng dẫn bạn phương pháp xét tương giao hiệu quả, cách xử lý biểu thức trị tuyệt đối và cung cấp ví dụ minh họa có đáp án chi tiết, giúp bạn làm chủ hoàn toàn dạng bài này trong các kỳ thi.
Bài toán 1: Biện luận số nghiệm của phương trình 
\(\left| f(x) \right| = f(m)\ \ \ (1)\) hoặc số giao điểm giữa đường thẳng \(y =
f(m)\) và đồ thị hàm số \(y = \left|
f(x) \right|\).
Phương pháp giải
Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị \(y = \left| f(x) \right|\) và đường thẳng \(y = f(m)\) (Đường thẳng \(y = f(m)\) song song hoặc trùng với trục \(Ox\)).
Bước 1: Vẽ đồ thị hàm số \(y = \left| f(x)
\right|\).
* Cách vẽ đồ thị hàm số \(y = \left| f(x)
\right|\) như sau:
+ Giữ nguyên đồ thị hàm số (C) nằm phía trên trục \(Ox\) ứng với \(f(x) \geq 0\).
+ Bỏ phần đồ thị phía dưới trục \(Ox\).
+ Lấy đối xứng phần bỏ đi đó qua \(Ox\) ứng với \(f(x) < 0\).
Hợp hai phần đồ thị trên là đồ thị hàm số \(y = \left| f(x) \right|\).
Bước 2: Xét tương giao dựa vào đồ thị.
Ví dụ minh họa: Cho đồ thị hàm số \(y =
f(x)\) (C) như hình vẽ bên.
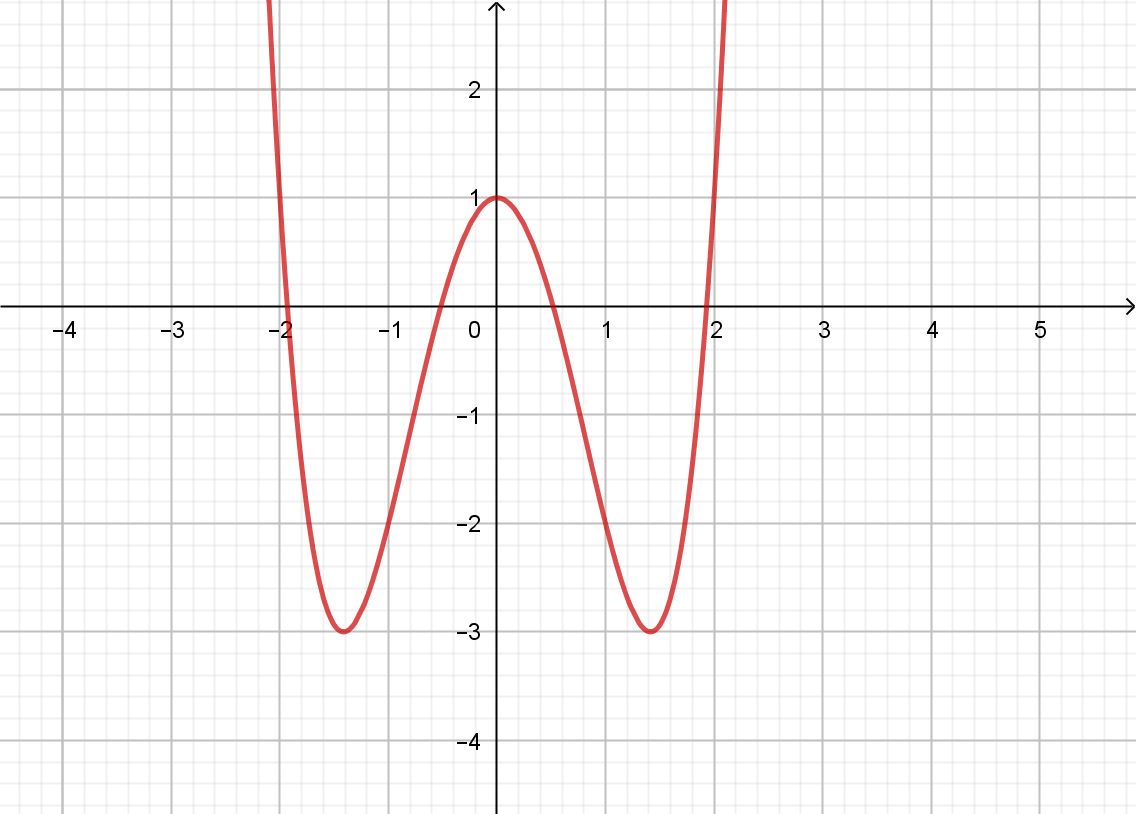
Biện luận số nghiệm của phương trình \(\left| f(x) \right| = f(m)\).
Hướng dẫn giải
* Cách vẽ đồ thị hàm số \(y = \left| f(x)
\right|\) như sau:
+ Giữ nguyên đồ thị hàm số (C) nằm phía trên trục \(Ox\) ứng với \(f(x) \geq 0\).
+ Bỏ phần đồ thị phía dưới trục \(Ox\).
+ Lấy đối xứng phần bỏ đi đó qua \(Ox\) ứng với \(f(x) < 0\).
Hợp hai phần đồ thị trên là đồ thị hàm số \(y = \left| f(x) \right|\).
* Dựa vào đồ thị:
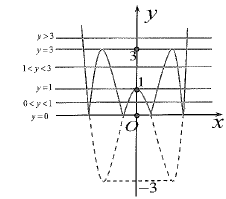
- Phương trình (*) vô nghiệm tức không có giao điểm \(\Leftrightarrow f(m) < 0\).
- Phương trình (*) có hai nghiệm phân biệt, tức có hai giao điểm \(\Leftrightarrow f(m) > 3\).
- Phương trình (*) có 4 nghiệm phân biệt, tức có bốn giao điểm \(\Leftrightarrow \left\lbrack \begin{matrix}
f(m) = 0 \\
f(m) = 3
\end{matrix} \right.\).
- Phương trình (*) có \(6\) nghiệm phân biệt tức có \(6\) giao điểm \(\Leftrightarrow 1 < f(m) < 3\).
- Phương trình (*) có \(7\) nghiệm phân biệt tức có \(7\) giao điểm \(\Leftrightarrow f(m) = 1\).
- Phương trình (*) có \(8\) nghiệm phân biệt tức có \(8\) giao điểm \(\Leftrightarrow 0 < f(m) < 1\).
Bài toán 2: Biện luận số nghiệm của phương trình \(f\left( |x| \right) = f(m)\ \ \ (2)\) hoặc số giao điểm giữa đường thẳng \(y =
f(m)\) và đồ thị hàm số \(y = f\left(
|x| \right)\).
Phương pháp giải:
Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị \(y = f\left( |x| \right)\) và đường thẳng \(y = f(m)\) (Đường thẳng \(y = f(m)\) song song hoặc trùng với trục \(Ox\)).
Bước 1: Vẽ đồ thị hàm số \(y = \left| f(x)
\right|\).
* Cách vẽ đồ thị hàm số \(y = \left| f(x)
\right|\) như sau:
+ Giữ nguyên đồ thị hàm số (C) nằm phía trên trục \(Ox\) ứng với \(f(x) \geq 0\).
+ Bỏ phần đồ thị phía dưới trục \(Ox\).
+ Lấy đối xứng phần bỏ đi đó qua \(Ox\) ứng với \(f(x) < 0\).
Hợp hai phần đồ thị trên là đồ thị hàm số \(y = \left| f(x) \right|\).
Bước 2: Xét tương giao dựa vào đồ thị.
Bài toán 3: Biện luận số nghiệm của phương trình \(\left| f\left( |x| \right) \right| = f(m)\ \ \
(3)\) hoặc số giao điểm giữa đường thẳng \(y = f(m)\) và đồ thị hàm số \(y = \left| f\left( |x| \right)
\right|\).
Phương pháp giải:
Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị \(y = f\left( |x| \right)\) và đường thẳng \(y = f(m)\) (Đường thẳng \(y = f(m)\) song song hoặc trùng với trục \(Ox\)).
Bước 1: Vẽ đồ thị hàm số \(y = \left| f(x)
\right|\).
* Cách vẽ đồ thị hàm số \(y = \left| f(x)
\right|\) như sau:
+ Giữ nguyên đồ thị hàm số (C) nằm phía trên trục \(Ox\) ứng với \(f(x) \geq 0\).
+ Bỏ phần đồ thị phía dưới trục \(Ox\).
+ Lấy đối xứng phần bỏ đi đó qua \(Ox\) ứng với \(f(x) < 0\).
Hợp hai phần đồ thị trên là đồ thị hàm số \(y = \left| f(x) \right|\).
Bước 2: Xét tương giao dựa vào đồ thị.
Ví dụ minh họa: Cho đồ thị hàm số \(y =
f(x)\) (C) như hình vẽ bên.
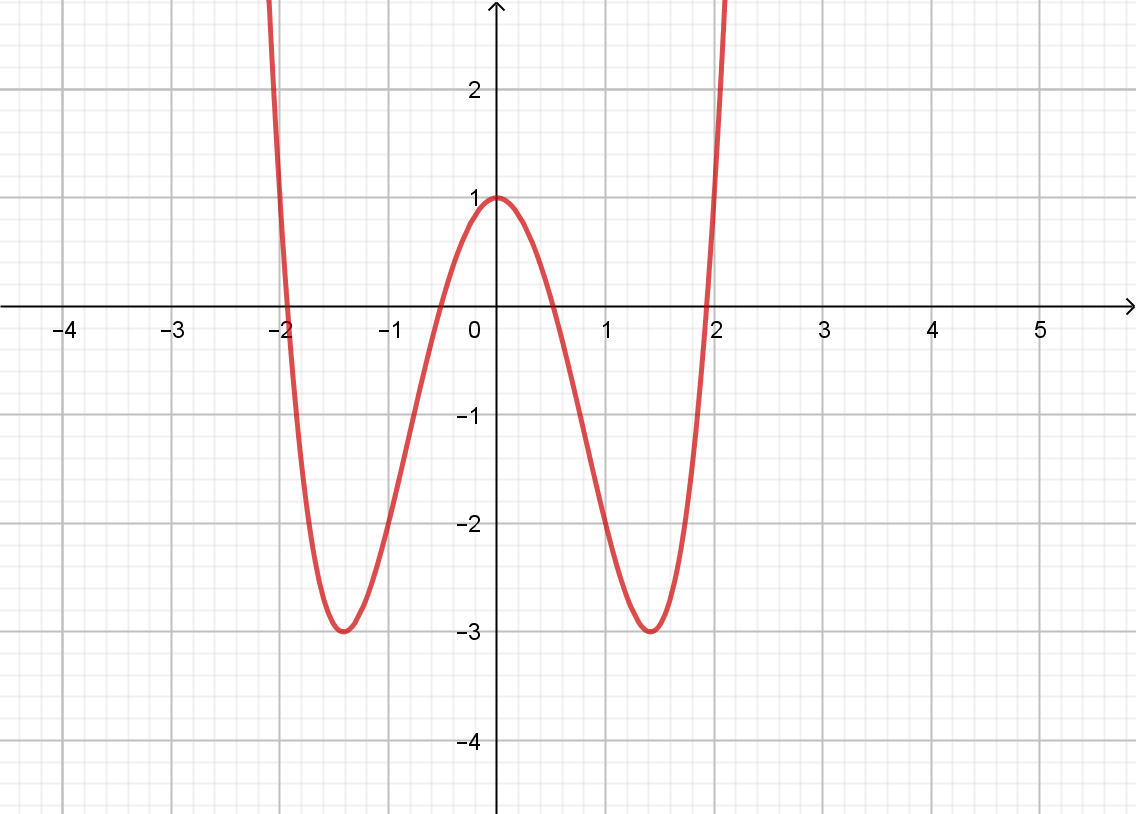
Biện luận số nghiệm của phương trình \(\left| f(x) \right| = f(m)\).
Hướng dẫn giải
* Cách vẽ đồ thị hàm số \(y = \left| f(x)
\right|\) như sau:
+ Giữ nguyên đồ thị hàm số (C) nằm phía trên trục \(Ox\) ứng với \(f(x) \geq 0\).
+ Bỏ phần đồ thị phía dưới trục \(Ox\).
+ Lấy đối xứng phần bỏ đi đó qua \(Ox\) ứng với \(f(x) < 0\).
Hợp hai phần đồ thị trên là đồ thị hàm số \(y = \left| f(x) \right|\).
* Dựa vào đồ thị:
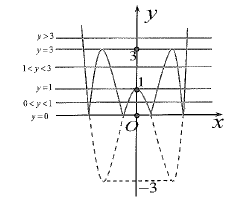
- Phương trình (*) vô nghiệm tức không có giao điểm \(\Leftrightarrow f(m) < 0\).
- Phương trình (*) có hai nghiệm phân biệt, tức có hai giao điểm \(\Leftrightarrow f(m) > 3\).
- Phương trình (*) có 4 nghiệm phân biệt, tức có bốn giao điểm \(\Leftrightarrow \left\lbrack \begin{matrix}
f(m) = 0 \\
f(m) = 3
\end{matrix} \right.\).
- Phương trình (*) có \(6\) nghiệm phân biệt tức có \(6\) giao điểm \(\Leftrightarrow 1 < f(m) < 3\).
- Phương trình (*) có \(7\) nghiệm phân biệt tức có \(7\) giao điểm \(\Leftrightarrow f(m) = 1\).
- Phương trình (*) có \(8\) nghiệm phân biệt tức có \(8\) giao điểm \(\Leftrightarrow 0 < f(m) < 1\).
------------------------------------------------------
Bài học về phương pháp xét tương giao dựa vào đồ thị hàm trị tuyệt đối không chỉ củng cố kiến thức khảo sát hàm số mà còn giúp bạn nâng cao kỹ năng phân tích hình học và đại số trong Toán 12. Hy vọng với phần hướng dẫn cụ thể và ví dụ chi tiết trong bài, bạn có thể hiểu rõ cách vẽ, cách xét và nhận biết số nghiệm dựa trên đồ thị.
👉 Hãy tiếp tục luyện tập thêm các dạng bài đồ thị hàm trị tuyệt đối khác để tự tin đạt điểm cao trong các bài kiểm tra và kỳ thi THPT Quốc gia!
