Cách bấm Casio tính diện tích mặt phẳng bằng tích phân
Casio tính diện tích mặt phẳng
Việc tính diện tích mặt phẳng bằng tích phân là một phần quan trọng trong chương trình Toán lớp 12, đặc biệt trong các đề thi THPT Quốc gia. Tuy nhiên, nhiều học sinh vẫn chưa biết cách bấm máy Casio để giải nhanh bài toán tích phân diện tích. Trong bài viết này, bạn sẽ được hướng dẫn chi tiết cách sử dụng Casio 570VN Plus hoặc tương đương để giải nhanh, chính xác và tránh sai sót. Cùng khám phá mẹo bấm máy đơn giản giúp tiết kiệm thời gian làm bài!
A. Cách bấm máy casio tích phân diện tích
Bài toán 1: Diện tích của mặt phẳng giới hạn bởi 
\(\left( C_{1} \right):y = f(x);\ \left( C_{2}
\right):y = g(x);x = a;x = b\) \((a
< b)\)
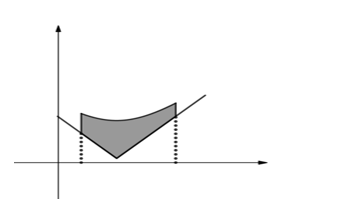
Công thức: \(S = \
\overset{b}{\int_{a}}\left| f(x) - g(x) \right|dx\)
Bài toán 2: Diện tích hình phẳng giới hạn bởi \(\begin{matrix}
\left\{ \begin{matrix}
(C_{1}):y = f(x) \\
(C_{2}):y = g(x) \\
(C_{3}):y = h(x) \\
\end{matrix} \right.\ \\
\\
\end{matrix}\)
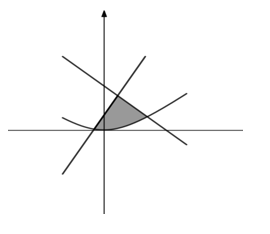
Bước 1: Tìm giao điểm của các đồ thị bằng cách giải các phương trình hoành độ giao điểm
Bước 2: Áp dụng công thức
\(S = \int_{a}^{c}\left| f(x) - h(x)
\right|dx + \int_{c}^{b}{\left| g(x) - h(x) \right|dx}\)
B. Bài tập áp dụng tính diện tích hình phẳng bằng máy tính cầm tay
Bài toán 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = x^{2} - 2x\) , trục hoành và hai đường thẳng \(x = 2;x = 0\).
Hướng dẫn giải
Áp dụng công thức: \(S =
\int_{0}^{2}{\left| x^{2} - 2x \right|dx}\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên
Bài toán 2: Tính diện tích giới hạn bởi đồ thị của các hàm số \(y = \frac{3x + 5}{2x + 2}\); \(y = 0\) ; \(x =
0\) và \(x = 2\)
A. \(S = ln2 + 3\) B. \(S = ln3 + 3\) C. \(S = ln3\) D. \(S
= ln3 - 2\)
Hướng dẫn giải
Diện tích mặt phẳng cần tìm: \(S =
\int_{0}^{2}\left| \frac{3x + 5}{2x + 2} \right|dx\)
Quan sát đáp án ta thấy có 3 đáp án chứa \(ln3\) nên ta tính \(\int_{0}^{2}\left| \frac{3x + 5}{2x + 2} \right|dx
- ln3\)
Sử dụng máy tính CASIO fx-580VN X để tính biểu thức trên
Đáp án: B
Bài toán 3. Tính diện tích mặt phẳng giới hạn bởi đồ thị của các hàm số \(\left\{ \begin{matrix}
(C_{1}):y = x^{2} + 1 \\
(C_{2}):y = x^{2} + 2x \\
x = 1;x = 2 \\
\end{matrix} \right.\)
Hướng dẫn giải
Diện tích mặt phẳng cần tìm \(S =
\int_{1}^{2}\left| (x^{2} + 1) - (x^{2} + 2x) \right|dx\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên:
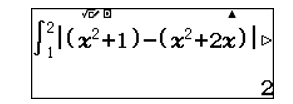
Bài toán 4. Tính diện tích hình phẳng giới hạn bởi \(\left\{ \begin{matrix}
(C_{1}):y = x^{2} + 2 \\
(C_{2}):y = 3x \\
\end{matrix} \right.\)
A. 2 B. 3 C.\(\frac{1}{2}\) D.\(\frac{1}{6}\)
Hướng dẫn giải
Sử dụng máy tính CASIO fx-580VN X để giải phương trình hoành độ giao điểm:
\(x^{2} + 2 = 3x \Leftrightarrow x^{2} -
3x + 2 = 0\)
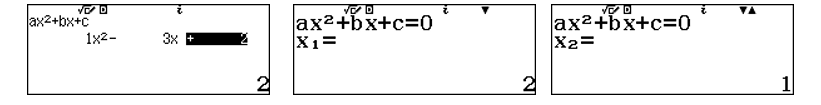
Khi đó : \(S = \int_{1}^{2}{\left| x^{2} -
3x + 2 \right|dx}\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên:
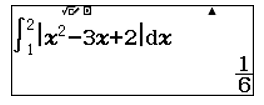
Đáp án D
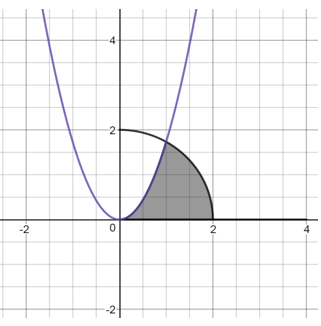
Bài toán 5. Tính diện tích hình phẳng giới hạn bởi parabol \(y = \sqrt{3}x^{2}\) , cung tròn có phương trình \(y = \sqrt{4 - x^{2}}\) (với \(0 \leq x \leq 2\) ) và trục hoành (như hình vẽ):
A.\(\frac{4\pi + \sqrt{3}}{12}\) B. \(\frac{4\pi - \sqrt{3}}{6}\)
C.\(\frac{4\pi + 2\sqrt{3} - 3}{6}\) D.\(\frac{5\sqrt{3} - 2\pi}{3}\)
Hướng dẫn giải
Sử dụng máy tính CASIO fx-580VN X tìm nghiệm của các phương trình hoành độ giao điểm
\(\sqrt{3}x^{2} = \sqrt{4 - x^{2}}
\Leftrightarrow 3x^{4} + x^{2} - 4 = 0\) (\(0 \leq x \leq 2\) ) \(\Rightarrow x = 1\)
\(\sqrt{3}x^{2} = 0 \Rightarrow x =
0\)
\(\sqrt{4 - x^{2}} = 0\) (\(0 \leq x \leq 2\)) \(\Rightarrow x = 2\)
Như vậy: Diện tích cần tìm \(S = \int_{0}^{1}{\sqrt{3}x^{2}}dx +
\int_{1}^{2}\sqrt{4 - x^{2}}dx\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên và lưu kết quả:
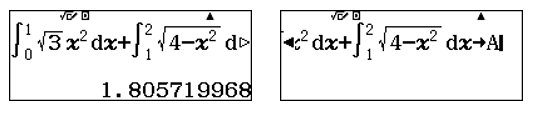
Thử các kết của đề bài ta có
 |
 \(\approx 0\) |
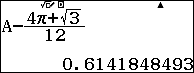Đáp án C | Đáp án D |
| LOẠI | NHẬN | Đã chọn đáp án B | |
---------------------------------
Qua bài viết trên, bạn đã nắm được cách bấm máy Casio tính diện tích mặt phẳng bằng tích phân một cách dễ hiểu và áp dụng được ngay vào bài tập. Đây là kỹ năng cực kỳ hữu ích giúp bạn rút ngắn thời gian làm bài và tăng độ chính xác trong phòng thi. Hãy luyện tập thêm nhiều ví dụ để thành thạo mẹo bấm máy này. Chúc bạn học tốt và đạt điểm tối đa trong môn Toán!
