Cách bấm máy tính Casio tính thể tích khối tròn xoay bằng tích phân
Bấm máy tính Casio tính thể tích khối tròn xoay
Trong chương trình Toán lớp 12, dạng bài tính thể tích khối tròn xoay bằng tích phân là một chủ đề quan trọng, thường xuyên xuất hiện trong đề thi THPT Quốc gia. Tuy nhiên, nhiều học sinh vẫn gặp khó khăn trong việc giải nhanh và chính xác dạng bài này. Bài viết này sẽ hướng dẫn bạn cách bấm máy tính Casio (570VN Plus, FX-580VN X...) để tính thể tích khối tròn xoay, giúp tiết kiệm thời gian và tránh sai sót khi làm bài thi trắc nghiệm. Cùng tìm hiểu ngay mẹo cực hay này!
A. Cách bấm máy tính tích phân thể tích
Dạng 1. Cho hình ![]() \((H)\) giới hạn bởi đồ thị của các hàm số
\((H)\) giới hạn bởi đồ thị của các hàm số ![]() \(y = f(x)\),
\(y = f(x)\), ![]() \(y = g(x)\) ,
\(y = g(x)\) , ![]() \(x = a;x = b\) quay quanh trục Ox tạo thành vật thể khối tròn xoay có thể tích bằng
\(x = a;x = b\) quay quanh trục Ox tạo thành vật thể khối tròn xoay có thể tích bằng
![]() \(V_{0x} = \pi\left| \int_{a}^{b}{\left(
\left\lbrack f(x) \right\rbrack^{2} - \left\lbrack g(x)
\right\rbrack^{2} \right)dx} \right|\)
\(V_{0x} = \pi\left| \int_{a}^{b}{\left(
\left\lbrack f(x) \right\rbrack^{2} - \left\lbrack g(x)
\right\rbrack^{2} \right)dx} \right|\)
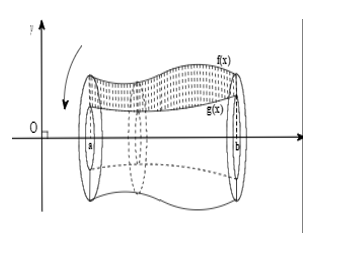
Dạng 2. Cho hình ![]() \((H)\) giới hạn bởi đồ thị của các hàm số
\((H)\) giới hạn bởi đồ thị của các hàm số ![]() \(x = f(y)\),
\(x = f(y)\), ![]() \(x = g(y)\) ,
\(x = g(y)\) , ![]() \(y = a;y = b\) quay quanh trục Oy tạo thành vật thể khối tròn xoay có thể tích bằng
\(y = a;y = b\) quay quanh trục Oy tạo thành vật thể khối tròn xoay có thể tích bằng
![]() \(V_{0y} = \pi\left| \int_{a}^{b}{\left(
\left\lbrack f(y) \right\rbrack^{2} - \left\lbrack g(y)
\right\rbrack^{2} \right)dy} \right|\)
\(V_{0y} = \pi\left| \int_{a}^{b}{\left(
\left\lbrack f(y) \right\rbrack^{2} - \left\lbrack g(y)
\right\rbrack^{2} \right)dy} \right|\)
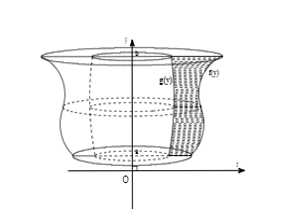
Chú ý: Nếu đề bài không có cho hai giả thiết ![]() \(x = a;x = b\)(hay
\(x = a;x = b\)(hay ![]() \(y = a;y = b\) ) thì trước khi áp dụng công thức
\(y = a;y = b\) ) thì trước khi áp dụng công thức ![]() \(V_{0x}\)(
\(V_{0x}\)(![]() \(V_{0y}\) ) ta phải tìm hai cận của tích phân bằng cách giải phương trình giao điểm
\(V_{0y}\) ) ta phải tìm hai cận của tích phân bằng cách giải phương trình giao điểm ![]() \(f(x) = g(x)\) (hoặc
\(f(x) = g(x)\) (hoặc ![]() \(f(y) = g(y)\) )
\(f(y) = g(y)\) )
Mở rộng:
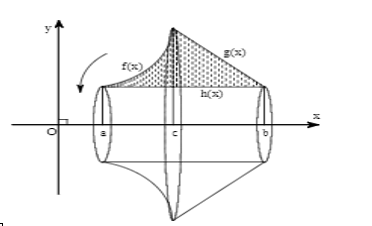
Bước 1: Tìm các giao điểm a, b,c là nghiệm của các phương trình ![]() \(f(x) = h(x);f(x) =
g(x)\) và
\(f(x) = h(x);f(x) =
g(x)\) và ![]() \(g(x) = h(x)\)
\(g(x) = h(x)\)
Bước 2: Áp dụng công thức
![]() \(V = \pi\left| \int_{a}^{b}{(\left\lbrack
f(x) \right\rbrack^{2}} - \left\lbrack g(x) \right\rbrack^{2})dx \right|
+ \pi\left| \int_{b}^{c}{(\left\lbrack g(x) \right\rbrack^{2}} -
\left\lbrack h(x) \right\rbrack^{2})dx \right|\)
\(V = \pi\left| \int_{a}^{b}{(\left\lbrack
f(x) \right\rbrack^{2}} - \left\lbrack g(x) \right\rbrack^{2})dx \right|
+ \pi\left| \int_{b}^{c}{(\left\lbrack g(x) \right\rbrack^{2}} -
\left\lbrack h(x) \right\rbrack^{2})dx \right|\)
B. Bài tập tính thể tích khối tròn xoay bằng máy tính cầm tay
Bài toán 1: Tính thể tích vật thể khối tròn xoay được tạo thành khi quay hình (H) giới hạn bởi đồ thị hàm số ![]() \(y =
\sqrt{sinx}\) , trục hoành,
\(y =
\sqrt{sinx}\) , trục hoành, ![]() \(x =
0\) và
\(x =
0\) và ![]() \(x = \frac{\pi}{2}\) quanh trục Ox.
\(x = \frac{\pi}{2}\) quanh trục Ox.
A.1 B. ![]() \(\frac{\pi}{2}\) C.
\(\frac{\pi}{2}\) C. ![]() \(2\pi\) D.
\(2\pi\) D. ![]() \(\pi\)
\(\pi\)
Hướng dẫn giải
Công thức tính thể tích ![]() \(V =
\pi\int_{0}^{\frac{\pi}{2}}{(\sqrt{sinx})^{2}dx}\)
\(V =
\pi\int_{0}^{\frac{\pi}{2}}{(\sqrt{sinx})^{2}dx}\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên
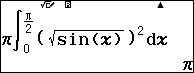
Đáp án: D
Bài toán 2: Cho miền D giới hạn bởi hai đồ thị![]() \(y = 4 - x^{2}\) và
\(y = 4 - x^{2}\) và ![]() \(y = x^{2} + 2\). Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox.
\(y = x^{2} + 2\). Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox.
C.![]() \(16\pi\) B.
\(16\pi\) B. ![]() \(\frac{8}{3}\pi\) C.
\(\frac{8}{3}\pi\) C. ![]() \(12\pi\) D.
\(12\pi\) D. ![]() \(\pi\)
\(\pi\)
cách bấm máy tính tích phân thể tích
Nhận xét: Vì đề bài không cho hai cận của tích phân do đó đầu tiên chúng ta phải tìm hoành độ giao điểm của hai hàm số đã cho
Dùng máy tính CASIO fx-580VN X để tìm nghiệm của phương trình: ![]() \(4 - x^{2} = x^{2} + 2\)
\(4 - x^{2} = x^{2} + 2\)
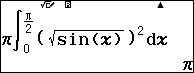
Công thức: ![]() \(V = \pi\left| \int_{-
1}^{1}\left\lbrack (4 - x^{2})^{2} - (x^{2} + 2)^{2} \right\rbrack dx
\right|\)
\(V = \pi\left| \int_{-
1}^{1}\left\lbrack (4 - x^{2})^{2} - (x^{2} + 2)^{2} \right\rbrack dx
\right|\)
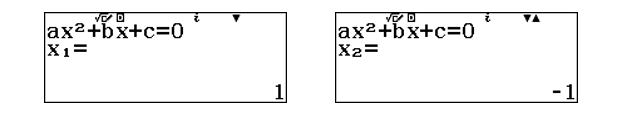
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên

Bài toán 3: Cho miền D giới hạn bởi hai đồ thị![]() \(y = x^{2}\);
\(y = x^{2}\); ![]() \(y
= 4x^{2}\) và
\(y
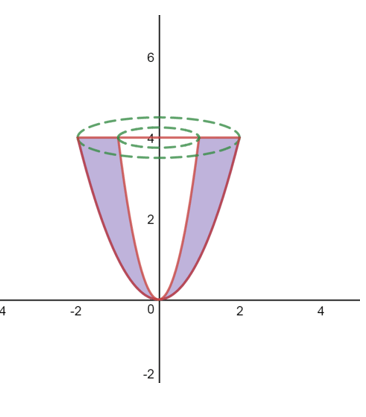
= 4x^{2}\) và ![]() \(y = 4\). Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Oy (như hình)
\(y = 4\). Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Oy (như hình)
A. ![]() \(12\pi\) B.
\(12\pi\) B. ![]() \(2\pi\) C.
\(2\pi\) C. ![]() \(6\pi\) D.
\(6\pi\) D. ![]() \(8\pi\)
\(8\pi\)
Hướng dẫn giải
Chuyển đổi hàm số:
![]() \(y = x^{2} \Rightarrow x =
\sqrt{y}\) và
\(y = x^{2} \Rightarrow x =
\sqrt{y}\) và ![]() \(y = 4x^{2} \Rightarrow
x = \frac{\sqrt{y}}{2}\)
\(y = 4x^{2} \Rightarrow
x = \frac{\sqrt{y}}{2}\)
Nhận xét ta có đồ thị ![]() \(y = x^{2}\) và
\(y = x^{2}\) và ![]() \(y = 4x^{2}\)giao nhau tại O.
\(y = 4x^{2}\)giao nhau tại O.
Do đó ta có  \(V = \pi\left|
\int_{0}^{4}\left( (\sqrt{y})^{2} - \left( \frac{\sqrt{y}}{2}
\right)^{2} \right)dy \right|\)
\(V = \pi\left|
\int_{0}^{4}\left( (\sqrt{y})^{2} - \left( \frac{\sqrt{y}}{2}
\right)^{2} \right)dy \right|\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên
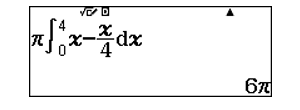
Đáp án: C
Nhận xét: Đối với một số biểu thức đơn giản ta có thể khai triển để việc bấm máy trở nên nhanh và dễ dàng hơn
Bài toán 4. Cho miền D giới hạn bởi đồ thị ![]() \((C):y = x^{2} + 1(x \geq 0)\)và hai đường thẳng
\((C):y = x^{2} + 1(x \geq 0)\)và hai đường thẳng ![]() \(y = - 3x + 11\) ;
\(y = - 3x + 11\) ;![]() \(y = 2\). Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox
\(y = 2\). Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox
Hướng dẫn giải
Hình vẽ minh họa
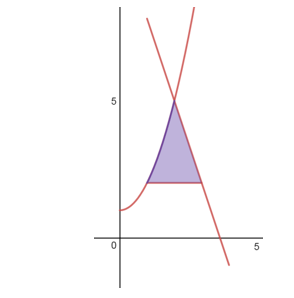
Tìm giao điểm của các đồ thị
 \(x^{2} + 1 = 2 \Rightarrow x = 1\) (vì
\(x^{2} + 1 = 2 \Rightarrow x = 1\) (vì  \(x > 0\) )
\(x > 0\) )
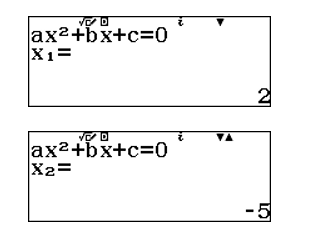
 \(- 3x + 11 = 2 \Rightarrow x =
3\)
\(- 3x + 11 = 2 \Rightarrow x =
3\) \(x^{2} + 1 = - 3x + 11 \Rightarrow x =
2\) (vì
\(x^{2} + 1 = - 3x + 11 \Rightarrow x =
2\) (vì  \(x = - 5 < 0\) )
\(x = - 5 < 0\) )
Công thức tính thể tích:
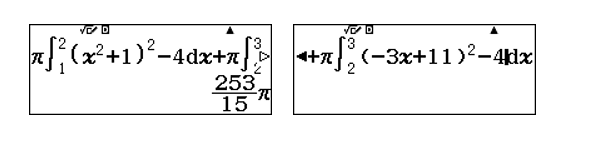
![]() \(V = \pi\int_{1}^{2}{\lbrack(x^{2} +
1)^{2} - 4\rbrack dx} + \int_{2}^{3}{\lbrack( - 3x + 11)^{2} - 4\rbrack
dx}\)
\(V = \pi\int_{1}^{2}{\lbrack(x^{2} +
1)^{2} - 4\rbrack dx} + \int_{2}^{3}{\lbrack( - 3x + 11)^{2} - 4\rbrack
dx}\)
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên
------------------------------------
Với hướng dẫn chi tiết trên, bạn đã biết cách sử dụng máy tính Casio để tính thể tích khối tròn xoay bằng tích phân một cách đơn giản và nhanh gọn. Đây là một kỹ năng không thể thiếu cho học sinh lớp 12 đang ôn thi THPT Quốc gia. Đừng quên luyện tập thêm nhiều ví dụ để làm chủ dạng toán này và nâng cao tốc độ làm bài. Chúc bạn học tốt và đạt điểm cao trong kỳ thi sắp tới!








