Cách khảo sát hàm số giá trị tuyệt đối
Hướng dẫn khảo sát hàm số giá trị tuyệt đối
Trong chương trình Toán 12, dạng bài hàm số giá trị tuyệt đối là một trong những chủ đề quan trọng, thường xuyên xuất hiện trong các kỳ kiểm tra và đề thi THPT Quốc gia. Việc khảo sát hàm số giá trị tuyệt đối giúp học sinh hiểu rõ cách xác định miền xác định, xét tính đơn điệu và vẽ đồ thị một cách chính xác.
Bài viết dưới đây sẽ hướng dẫn chi tiết cách khảo sát hàm số giá trị tuyệt đối từng bước, kết hợp với ví dụ minh họa cụ thể, giúp bạn dễ hiểu, dễ áp dụng và ghi nhớ lâu. Đây là tài liệu chuyên đề Toán 12 hữu ích, phù hợp cho học sinh muốn nắm chắc kiến thức và luyện thi hiệu quả.
Bài toán: Dựa vào đồ thị hàm số 
\(y =
f(x)\), xác định đồ thị hàm số có chứa dấu giá trị tuyệt đối.
Dạng 1: Từ đồ thị \((C):y = f(x)\), suy ra đồ thị \((C'):y = \left| f(x)
\right|\)
Ta có: \(y = \left| f(x) \right| = \left\{
\begin{matrix}
f(x)\ \ \ \ \ \ khi\ \ f(x) \geq 0 \\
- f(x)\ \ \ khi\ \ f(x) < 0
\end{matrix} \right.\)
Do đó, đồ thị \((C'):y = \left| f(x)
\right|\) bao gồm:
+ Phần đồ thị \((C)\) nằm phía trên trục hoành (cả những điểm nằm trên trục hoành).
+ Phần đối xứng với phần đồ thị (C) nằm phía dưới trục hoành qua trục hoành.
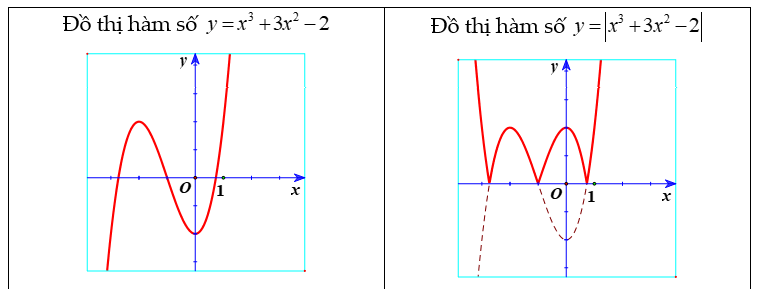
Nhận xét: \(y = \left| f(x) \right| \geq
0\) nên toàn bộ phần đồ thị \((C')\) đều nằm phía trên trục hoành.
Dạng 2: Từ đồ thị \((C):y = f(x)\) , suy ra đồ thị \((C'):y = f\left( |x| \right)\)
Ta có: \(y = f\left( |x| \right) = \left\{
\begin{matrix}
f(x)\ \ \ \ \ \ khi\ \ x \geq 0 \\
f( - x)\ \ \ khi\ \ x < 0
\end{matrix} \right.\)
Do đó, đồ thị \((C'):y = f\left( |x|
\right)\) bao gồm:
+ Phần đồ thị (C) nằm bên phải trục tung (cả những điểm nằm trên trục tung).
+ Phần đối xứng với phần đồ thị (C) nằm bên phải trục tung qua trục tung.
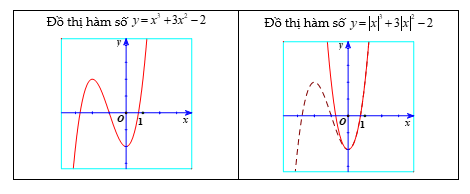
Nhận xét: \(y = f\left( |x|
\right)\) là hàm số chẵn nên đồ thị \((C')\) nhận trục tung làm trục đối xứng.
Dạng 3: Từ đồ thị (C): y = f(x) , suy ra đồ thị \((C'):y = \left| f\left( |x| \right)
\right|\)
Để có được đồ thị \((C'):y = f\left(
|x| \right)\), ta áp dụng hai dạng 1, 2.
Cụ thể:
+ Từ đồ thị thị (C): y = f(x) \(\Rightarrow\) đồ thị \((C''):y = \left| f(x) \right| = g(x)
\Rightarrow\) Đồ thị\(\ (C'):y =
g\left( |x| \right) = \left| f\left( |x| \right) \right|\).
+ Từ đồ thị thị (C): y = f(x) \(\Rightarrow\) Đồ thị \((C''):y = f\left( |x| \right) =
h(x)\) đồ thị \((C'):y = \left| h(x) \right| = \left| f\left(
|x| \right) \right|\).
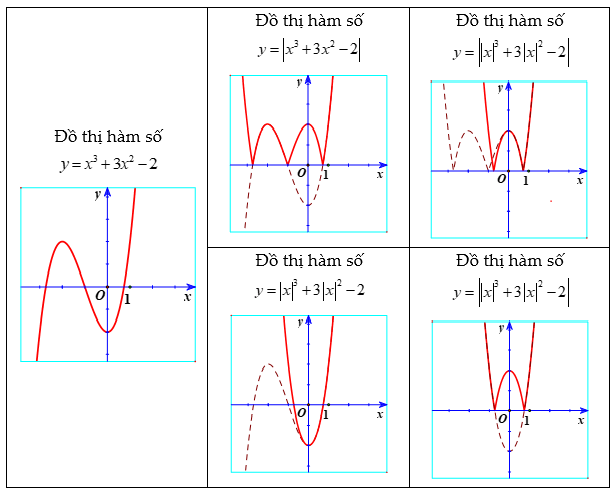
Nhận xét: Đồ thị \(y = \left| f\left( |x|
\right) \right|\) nằm phía trên trục hoành và nhận trục tung làm trục đối xứng.
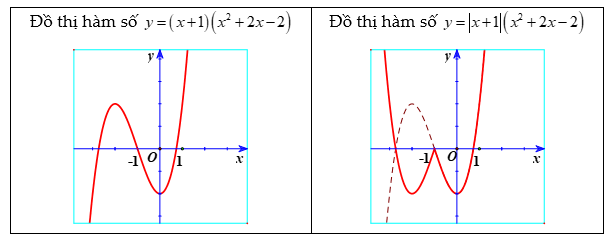
Dạng 4: Từ đồ thị \((C):y =
u(x).v(x)\), suy ra đồ thị \((C'):y
= \left| u(x) \right|.v(x)\)
Ta có: \(\left| u(x) \right| = \left\{
\begin{matrix}
u(x)\ \ \ \ \ \ khi\ \ u(x) \geq 0 \\
- u(x)\ \ \ khi\ \ u(x) < 0
\end{matrix} \right.\)
Do đó, đồ thị (c’): y =| f(x)| bao gồm:
+ Phần đồ thị (c) nằm trên miền \(u(x) \geq
0\).
+ Phần đối xứng với phần đồ thị (c) nằm trên miền \(u(x) < 0\) qua trục hoành.
-------------------------------------------------------------
Qua bài viết Cách khảo sát hàm số giá trị tuyệt đối, bạn đã nắm vững phương pháp nhận dạng, chia miền, xét đạo hàm và vẽ đồ thị chi tiết cho từng trường hợp. Hãy tiếp tục luyện tập với các dạng bài mở rộng về hàm số giá trị tuyệt đối Toán 12, kết hợp cùng chuyên đề đạo hàm – cực trị – tiệm cận để củng cố kỹ năng và đạt điểm cao trong kỳ thi sắp tới.
