Chuyên đề Xét tương giao dựa vào đồ thị của hàm số trị tuyệt đối Toán 12
Dạng toán Tương giao trong hàm trị tuyệt đối - có đáp án
Trong chương trình Toán 12, chuyên đề xét tương giao dựa vào đồ thị của hàm số trị tuyệt đối là một nội dung quan trọng, thường xuất hiện trong các đề thi THPT Quốc gia. Dạng bài này giúp học sinh hiểu rõ mối quan hệ giữa đồ thị và số nghiệm của phương trình, đồng thời rèn luyện tư duy hình học – đại số. Bài viết dưới đây sẽ hướng dẫn chi tiết phương pháp xét tương giao hiệu quả, cách phân tích đồ thị hàm trị tuyệt đối nhanh, kèm ví dụ minh họa và đáp án chi tiết, giúp bạn dễ dàng nắm vững kiến thức và làm bài chính xác.
A. Ví dụ minh họa xét tương giao dựa vào đồ thị hàm trị tuyệt đối
Ví dụ 1. Cho hàm số ![]() \(y = f(x) = ax^{4} +
bx^{2} + c\)
\(y = f(x) = ax^{4} +
bx^{2} + c\) ![]() \((a \neq 0)\) có đồ thị như hình bên:
\((a \neq 0)\) có đồ thị như hình bên:
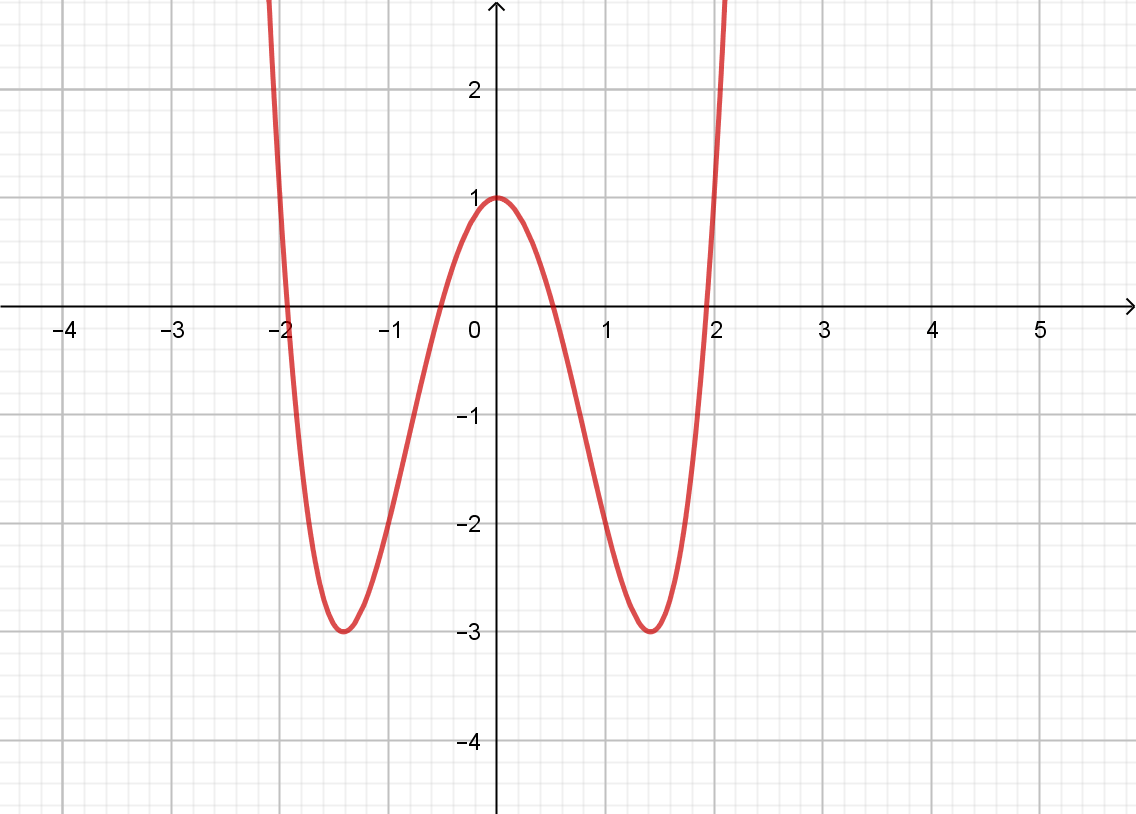
Tất cả các giá trị của ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| f(x) \right| =
m\) có
\(\left| f(x) \right| =
m\) có ![]() \(4\) nghiệm phân biệt là:
\(4\) nghiệm phân biệt là:
A. ![]() \(\left\lbrack \begin{matrix}
m = 0 \\
m = 3
\end{matrix} \right.\). B.
\(\left\lbrack \begin{matrix}
m = 0 \\
m = 3
\end{matrix} \right.\). B. ![]() \(1 < m
< 3\). C.
\(1 < m
< 3\). C. ![]() \(- 3 < m <
1\). D.
\(- 3 < m <
1\). D. ![]() \(m = 3\).
\(m = 3\).
Hướng dẫn giải
Chọn A.
Ta có đồ thị của hàm số ![]() \(y = \left| f(x)
\right|\) như sau:
\(y = \left| f(x)
\right|\) như sau:
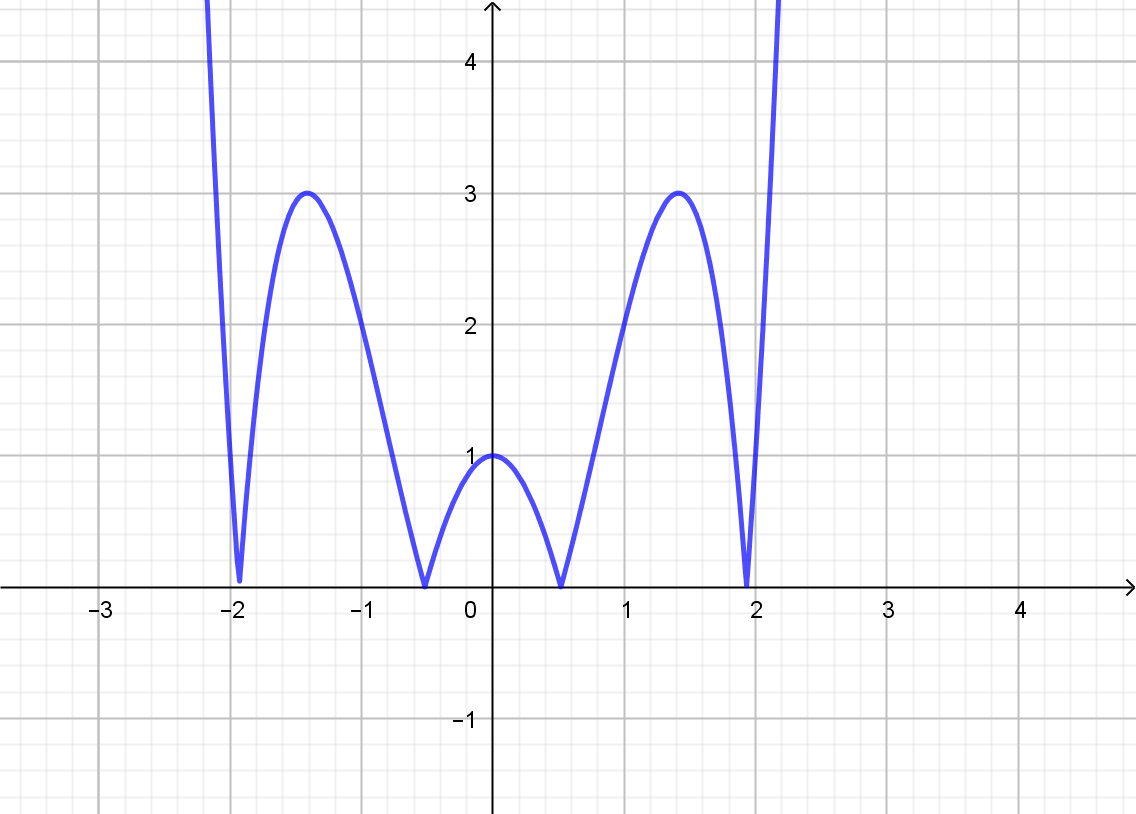
Số nghiệm của phương trình ![]() \(\left| f(x)
\right| = m\) là số giao điểm của đồ thị hàm số
\(\left| f(x)
\right| = m\) là số giao điểm của đồ thị hàm số ![]() \(y = \left| f(x) \right|\) và đường thẳng
\(y = \left| f(x) \right|\) và đường thẳng ![]() \(y = m\).
\(y = m\).
Dựa vào đồ thị ta thấy phương trình ![]() \(\left| f(x) \right| = m\) có
\(\left| f(x) \right| = m\) có ![]() \(4\) nghiệm phân biệt
\(4\) nghiệm phân biệt ![]() \(\Leftrightarrow \left\lbrack \begin{matrix}
m = 0 \\
m = 3
\end{matrix} \right.\).
\(\Leftrightarrow \left\lbrack \begin{matrix}
m = 0 \\
m = 3
\end{matrix} \right.\).
Ví dụ 2. Cho hàm số ![]() \(y = f(x) = ax^{4} +
bx^{2} + c\)
\(y = f(x) = ax^{4} +
bx^{2} + c\) ![]() \((a \neq 0)\) có đồ thị như hình bên:
\((a \neq 0)\) có đồ thị như hình bên:
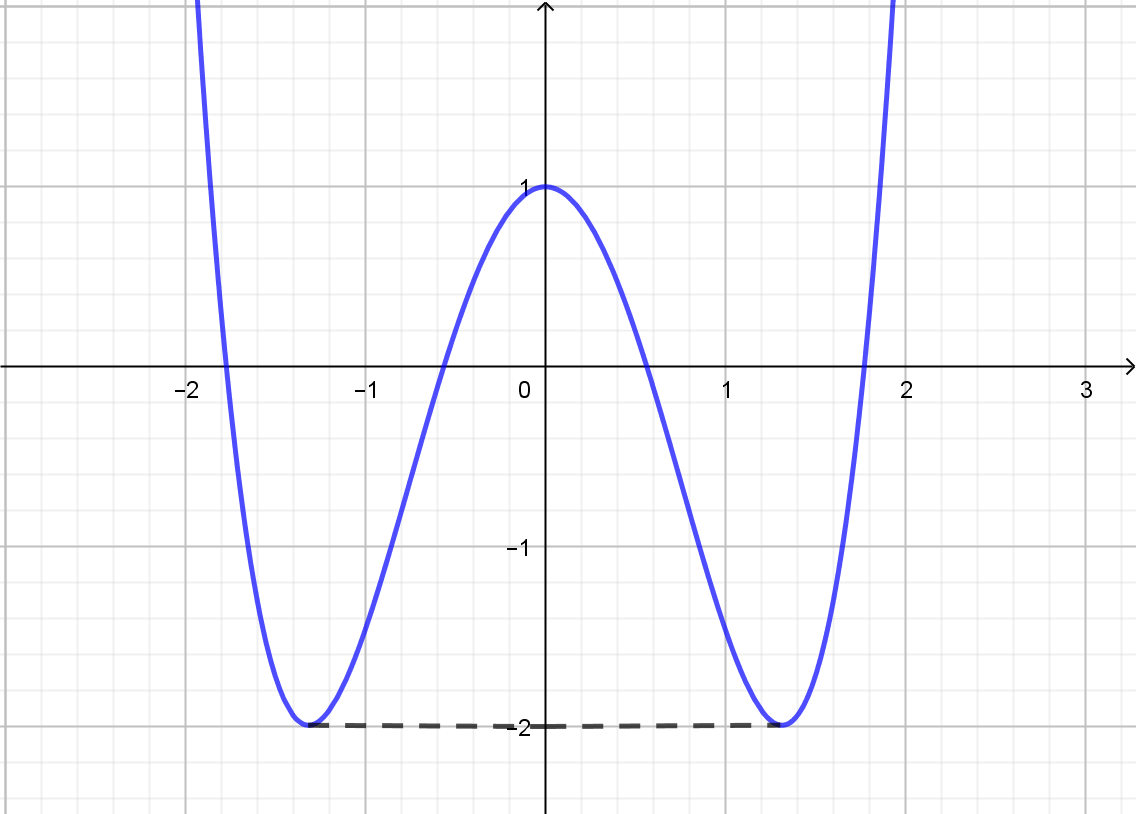
Tất cả các giá trị của ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| f(x) \right| - m + 1 =
0\) có
\(\left| f(x) \right| - m + 1 =
0\) có ![]() \(8\) nghiệm phân biệt là:
\(8\) nghiệm phân biệt là:
A. ![]() \(0 < m < 1\). B.
\(0 < m < 1\). B. ![]() \(1 < m < 2\). C.
\(1 < m < 2\). C. ![]() \(0 \leq m \leq 1\). D.
\(0 \leq m \leq 1\). D. ![]() \(1 \leq m \leq 2\).
\(1 \leq m \leq 2\).
Hướng dẫn giải
Chọn B.
Ta có đồ thị của hàm số ![]() \(y = \left| f(x)
\right|\) như sau:
\(y = \left| f(x)
\right|\) như sau:
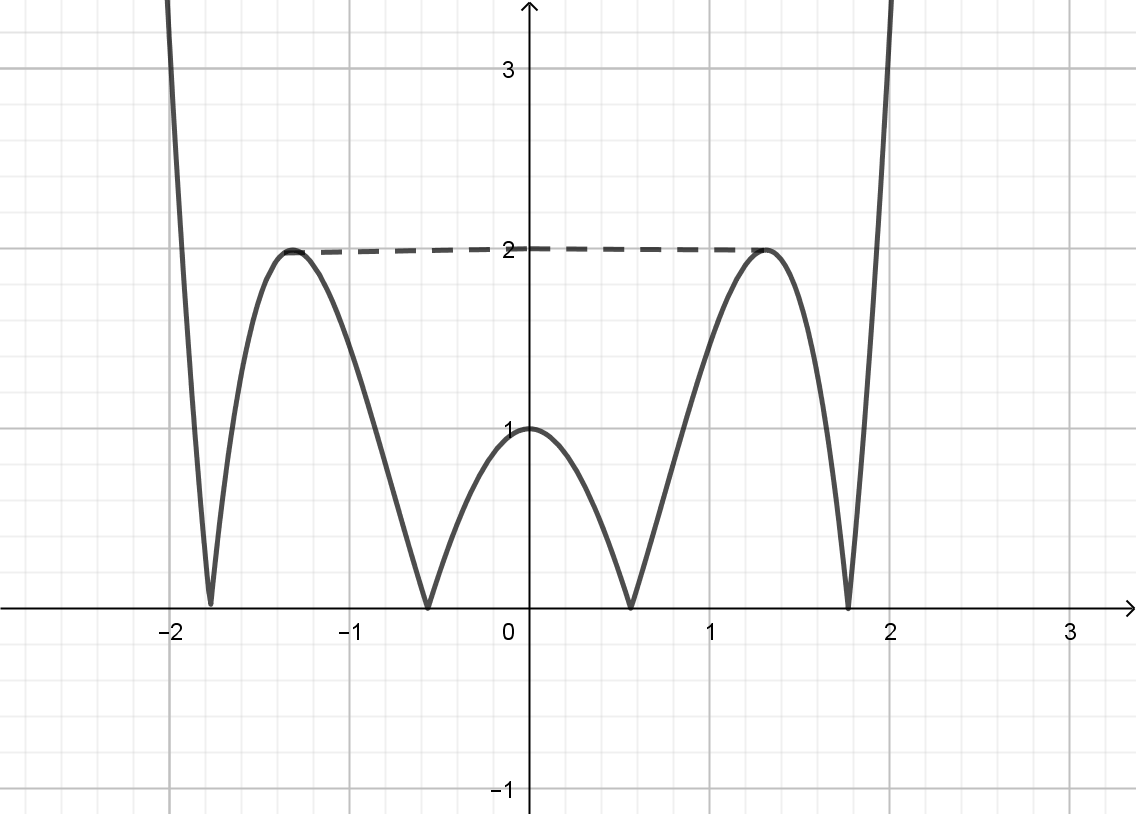
Số nghiệm của phương trình ![]() \(\left| f(x)
\right| - m + 1 = 0\) là số giao điểm của đồ thị hàm số
\(\left| f(x)
\right| - m + 1 = 0\) là số giao điểm của đồ thị hàm số ![]() \(y = \left| f(x) \right|\) và đường thẳng
\(y = \left| f(x) \right|\) và đường thẳng ![]() \(y = m - 1\).
\(y = m - 1\).
Dựa vào đồ thị ta thấy phương trình ![]() \(\left| f(x) \right| - m + 1 = 0\) có
\(\left| f(x) \right| - m + 1 = 0\) có ![]() \(8\) nghiệm phân biệt
\(8\) nghiệm phân biệt
![]() \(\Leftrightarrow 0 < m - 1 < 1
\Leftrightarrow 1 < m < 2\).
\(\Leftrightarrow 0 < m - 1 < 1
\Leftrightarrow 1 < m < 2\).
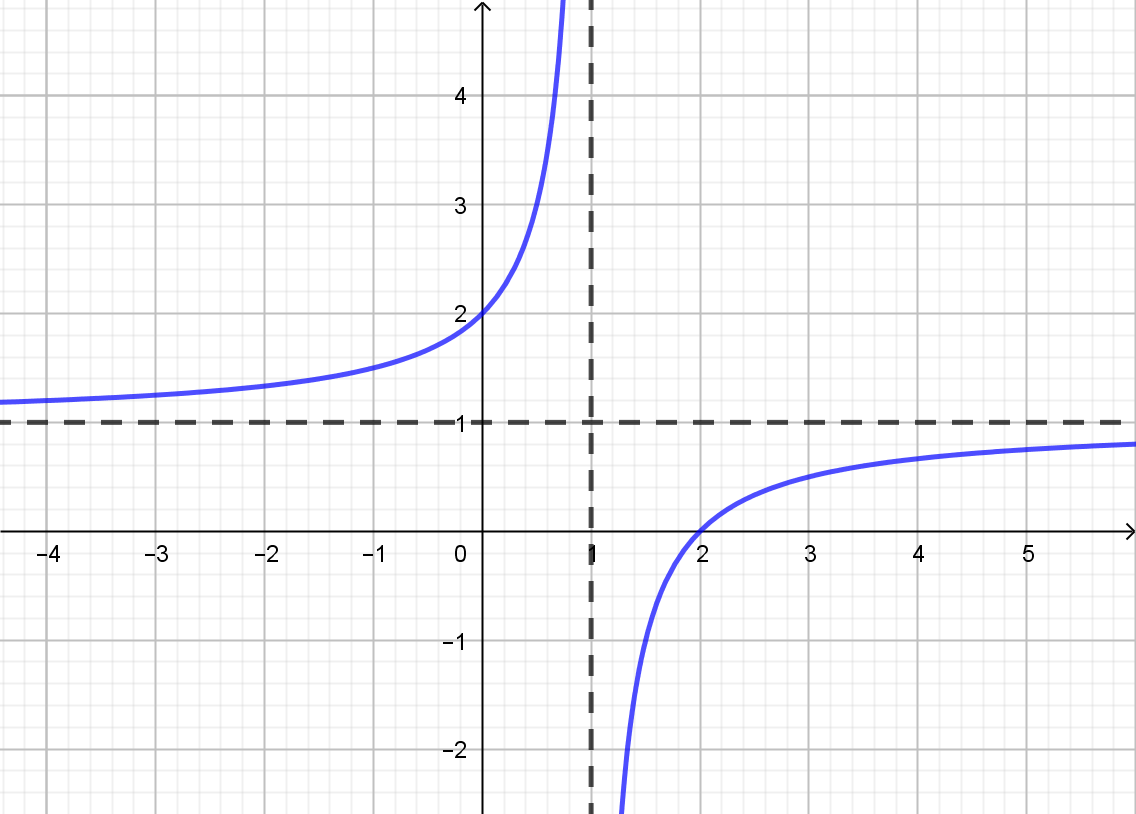
Ví dụ 3. Cho hàm số ![]() \(y = f(x) = \frac{ax +
b}{cx + d}\) có đồ thị như hình bên:
\(y = f(x) = \frac{ax +
b}{cx + d}\) có đồ thị như hình bên:
Tất cả các giá trị của ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| f(x) \right| =
m\) có
\(\left| f(x) \right| =
m\) có ![]() \(2\) nghiệm phân biệt là:
\(2\) nghiệm phân biệt là:
A. ![]() \(\left\lbrack \begin{matrix}
m \geq 2 \\
m \leq 1
\end{matrix} \right.\). B.
\(\left\lbrack \begin{matrix}
m \geq 2 \\
m \leq 1
\end{matrix} \right.\). B. ![]() \(\left\lbrack \begin{matrix}
0 < m < 1 \\
m > 1
\end{matrix} \right.\). C.
\(\left\lbrack \begin{matrix}
0 < m < 1 \\
m > 1
\end{matrix} \right.\). C. ![]() \(\left\lbrack \begin{matrix}
m > 2 \\
m < 1
\end{matrix} \right.\). D.
\(\left\lbrack \begin{matrix}
m > 2 \\
m < 1
\end{matrix} \right.\). D. ![]() \(0 < m
< 1\).
\(0 < m
< 1\).
Hướng dẫn giải
Chọn B.
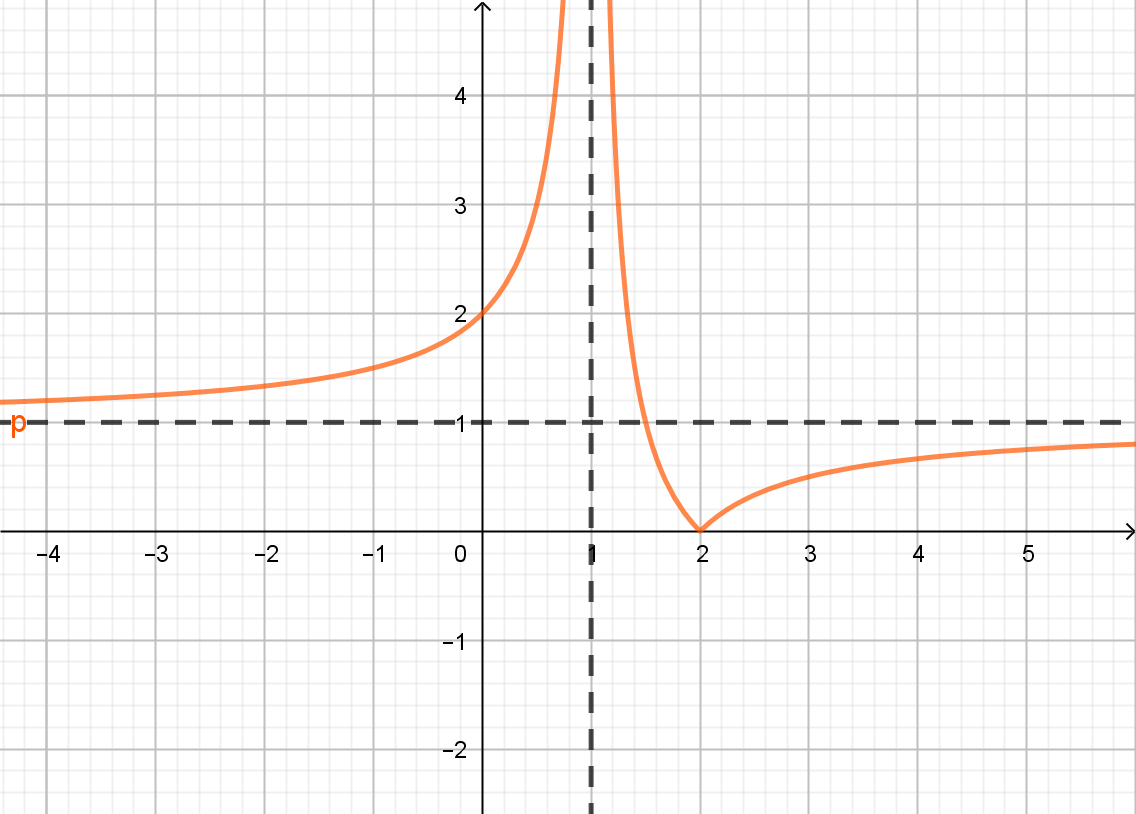
Ta có đồ thị của hàm số ![]() \(y = \left| f(x)
\right|\) như sau:
\(y = \left| f(x)
\right|\) như sau:
Số nghiệm của phương trình ![]() \(\left| f(x)
\right| = m\) là số giao điểm của đồ thị hàm số
\(\left| f(x)
\right| = m\) là số giao điểm của đồ thị hàm số ![]() \(y = \left| f(x) \right|\) và đường thẳng
\(y = \left| f(x) \right|\) và đường thẳng ![]() \(y = m\).
\(y = m\).
Dựa vào đồ thị ta thấy phương trình ![]() \(\left| f(x) \right| = m\) có
\(\left| f(x) \right| = m\) có ![]() \(2\) nghiệm phân biệt
\(2\) nghiệm phân biệt ![]() \(\Leftrightarrow \left\lbrack \begin{matrix}
0 < m < 1 \\
m > 1
\end{matrix} \right.\).
\(\Leftrightarrow \left\lbrack \begin{matrix}
0 < m < 1 \\
m > 1
\end{matrix} \right.\).
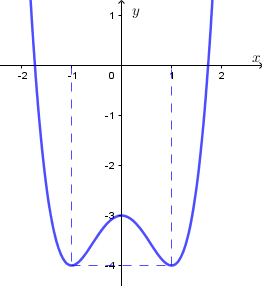
Ví dụ 4. Cho hàm số ![]() \(y = f(x)\) có đồ thị như đường cong trong hình dưới đây:
\(y = f(x)\) có đồ thị như đường cong trong hình dưới đây:
Tìm tất cả các giá trị thực của tham số ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| f(x) \right| = m\) có
\(\left| f(x) \right| = m\) có ![]() \(6\) nghiệm phân biệt:
\(6\) nghiệm phân biệt:
A. ![]() \(- 4 < m <- 3\). B.
\(- 4 < m <- 3\). B. ![]() \(0 < m < 3\). C.
\(0 < m < 3\). C. ![]() \(m > 4\). D.
\(m > 4\). D. ![]() \(3 < m < 4\).
\(3 < m < 4\).
Hướng dẫn giải
Chọn D
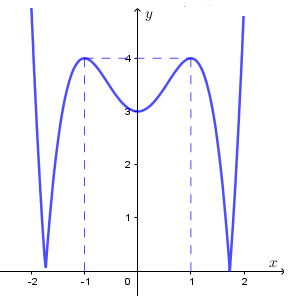
Đồ thị hàm số ![]() \(y = \left| f(x)
\right|\) có được bằng cách: giữ nguyên phần đồ thị hàm số
\(y = \left| f(x)
\right|\) có được bằng cách: giữ nguyên phần đồ thị hàm số ![]() \(y = f(x)\) nằm trên trục hoành, lấy đối xứng phần dưới trục hoành qua trục hoành.
\(y = f(x)\) nằm trên trục hoành, lấy đối xứng phần dưới trục hoành qua trục hoành.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số ![]() \(y = \left| f(x) \right|\) và đường thẳng
\(y = \left| f(x) \right|\) và đường thẳng ![]() \(y = m\).
\(y = m\).
Dựa vào đồ thị hàm số, phương trình có ![]() \(6\) nghiệm khi
\(6\) nghiệm khi ![]() \(3 < m < 4\).
\(3 < m < 4\).
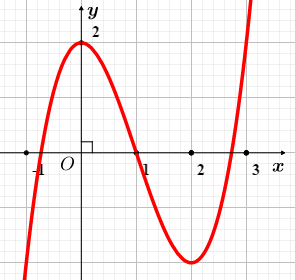
Ví dụ 5. Tìm tất cả giá trị thực của tham số ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| x^{3} - 3x^{2} + 2 \right| - m = 1\) có
\(\left| x^{3} - 3x^{2} + 2 \right| - m = 1\) có ![]() \(6\) nghiệm phân biệt.
\(6\) nghiệm phân biệt.
A. ![]() \(- 2 < m < 0\). B.
\(- 2 < m < 0\). B. ![]() \(1 < m < 3\). C.
\(1 < m < 3\). C. ![]() \(0 < m < 2\). D.
\(0 < m < 2\). D. ![]() \(- 1 < m < 1\).
\(- 1 < m < 1\).
Hướng dẫn giải
Chọn D
Ta có: ![]() \(\left| x^{3} - 3x^{2} + 2 \right|
- m = 1 \Leftrightarrow \left| x^{3} - 3x^{2} + 2 \right| = m +
1\)
\(\left| x^{3} - 3x^{2} + 2 \right|
- m = 1 \Leftrightarrow \left| x^{3} - 3x^{2} + 2 \right| = m +
1\) ![]() \((*)\).
\((*)\).
Số nghiệm của phương trình ![]() \((*)\) bằng số điểm chung giữa đồ thị
\((*)\) bằng số điểm chung giữa đồ thị ![]() \((C)\) của hàm số
\((C)\) của hàm số ![]() \(y = \left| x^{3} - 3x^{2} + 2
\right|\) và đường thẳng
\(y = \left| x^{3} - 3x^{2} + 2
\right|\) và đường thẳng ![]() \(d:y = m +
1\).
\(d:y = m +
1\).
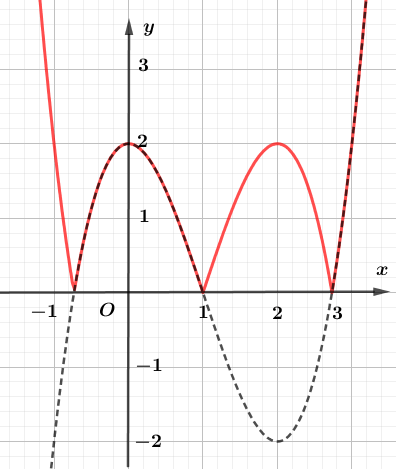
Đồ thị hàm số ![]() \((C)\) có được bằng cách lấy đối xứng phần đồ thị hàm số
\((C)\) có được bằng cách lấy đối xứng phần đồ thị hàm số ![]() \(y =
x^{3} - 3x^{2} + 2\) nằm phía dưới trục hoành qua trục hoành, ta được đồ thị hàm số (nét liền) như hình vẽ bên dưới.
\(y =
x^{3} - 3x^{2} + 2\) nằm phía dưới trục hoành qua trục hoành, ta được đồ thị hàm số (nét liền) như hình vẽ bên dưới.
Dựa vào đồ thị hàm số ta thấy đường thẳng ![]() \(y = m + 1\) có
\(y = m + 1\) có ![]() \(6\) điểm chung với đồ thị hàm số
\(6\) điểm chung với đồ thị hàm số ![]() \((C)\) khi và chỉ khi
\((C)\) khi và chỉ khi ![]() \(0 < m + 1 < 2 \Leftrightarrow - 1 < m
< 1\).
\(0 < m + 1 < 2 \Leftrightarrow - 1 < m
< 1\).
B. Bài tập tự rèn luyện có đáp án cụ thể
Bài tập 1. Cho hàm số ![]() \(y = f(x)\) xác định, liên tục trên
\(y = f(x)\) xác định, liên tục trên ![]() \(\mathbb{R}\) và có bảng biến thiên như sau:
\(\mathbb{R}\) và có bảng biến thiên như sau:
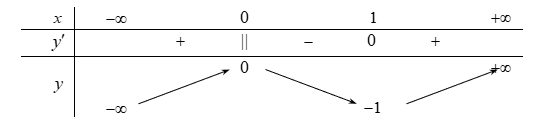
Tìm các giá trị thực của tham số ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| f(x) \right| = m + 2\) có bốn nghiệm phân biệt
\(\left| f(x) \right| = m + 2\) có bốn nghiệm phân biệt
A. ![]() \(- 2 < m < - 1\). B.
\(- 2 < m < - 1\). B. ![]() \(- 3 \leq m \leq - 2\). C.
\(- 3 \leq m \leq - 2\). C. ![]() \(- 2 \leq m \leq - 1\). D.
\(- 2 \leq m \leq - 1\). D. ![]() \(- 3 < m < - 2\)
\(- 3 < m < - 2\)
Bài tập 2. Cho hàm số ![]() \(y =
\frac{1}{4}x^{4} - 2x^{2} + 3\) có đồ thị như hình dưới:
\(y =
\frac{1}{4}x^{4} - 2x^{2} + 3\) có đồ thị như hình dưới:
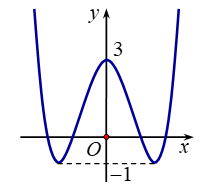
Tổng tất cả các giá trị nguyên của tham số ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\left| x^{4} - 8x^{2} + 12
\right| = m\) có
\(\left| x^{4} - 8x^{2} + 12
\right| = m\) có ![]() \(8\) nghiệm phân biệt là
\(8\) nghiệm phân biệt là
A. ![]() \(3\). B.
\(3\). B. ![]() \(6\). C.
\(6\). C. ![]() \(10\). D.
\(10\). D. ![]() \(0\).
\(0\).
Bài tập 3. Cho hàm số ![]() \(f(x)\) có đồ thị như hình vẽ dưới đây:
\(f(x)\) có đồ thị như hình vẽ dưới đây:
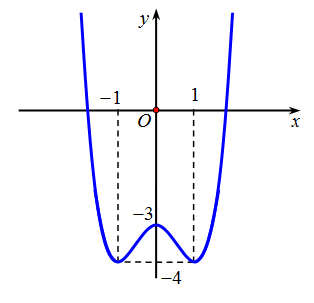
Phương trình ![]() \(\left| f(x) \right| =
\pi\) có bao nhiêu nghiệm thực phân biệt.
\(\left| f(x) \right| =
\pi\) có bao nhiêu nghiệm thực phân biệt.
A. ![]() \(3\). B.
\(3\). B. ![]() \(2\). C.
\(2\). C. ![]() \(6\). D.
\(6\). D. ![]() \(4\).
\(4\).
Bài tập 4. Hình bên là đồ thị của hàm số ![]() \(y = \frac{2x - 1}{x - 1}\).
\(y = \frac{2x - 1}{x - 1}\).
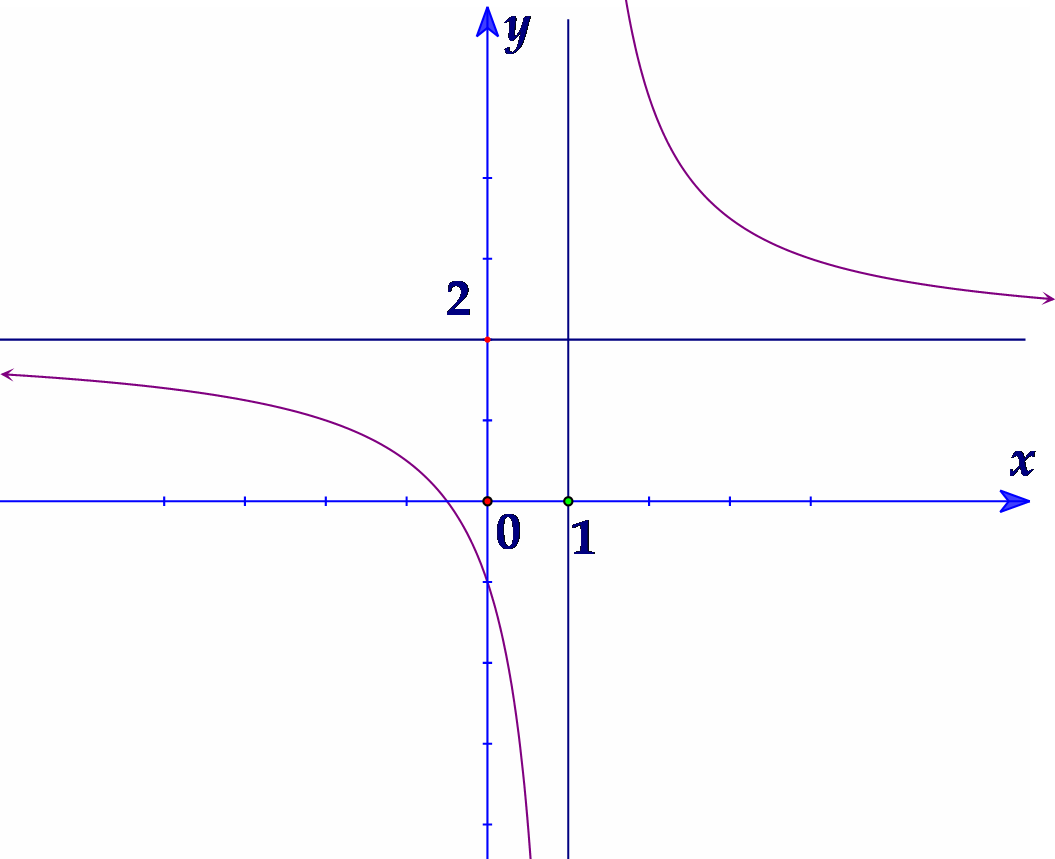
Tìm tất cả các giá trị thực của tham số ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(\frac{|2x + 1|}{x - 1} = 3m -
1\) có hai nghiệm phân biệt.
\(\frac{|2x + 1|}{x - 1} = 3m -
1\) có hai nghiệm phân biệt.
A. ![]() \(- \frac{1}{3} < m <
\frac{1}{3}\). B. Không có
\(- \frac{1}{3} < m <
\frac{1}{3}\). B. Không có ![]() \(m\). C.
\(m\). C. ![]() \(m >
1\). D.
\(m >
1\). D. ![]() \(- 2 < m <
0\).
\(- 2 < m <
0\).
Bài tập 5. Cho đồ thị hàm số ![]() \(y = f(x) = -
x^{3} + 3x - 2\) như hình vẽ:
\(y = f(x) = -
x^{3} + 3x - 2\) như hình vẽ:
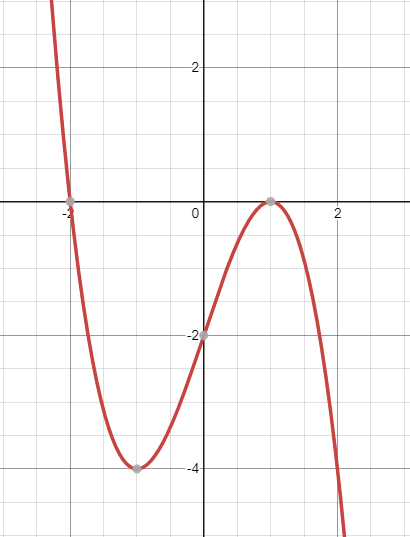
Phương trình ![]() \(|x + 2|(x - 1)^{2} =
m\) có đúng
\(|x + 2|(x - 1)^{2} =
m\) có đúng ![]() \(2\) nghiệm phân biệt khi và chỉ khi:
\(2\) nghiệm phân biệt khi và chỉ khi:
A. ![]() \(\left\lbrack \begin{matrix}
m < 0 \\
m = 4
\end{matrix} \right.\). B.
\(\left\lbrack \begin{matrix}
m < 0 \\
m = 4
\end{matrix} \right.\). B. ![]() \(0 \leq m
\leq 4\). C.
\(0 \leq m
\leq 4\). C. ![]() \(\left\lbrack
\begin{matrix}
m > 4 \\
m = 0
\end{matrix} \right.\). D.
\(\left\lbrack
\begin{matrix}
m > 4 \\
m = 0
\end{matrix} \right.\). D. ![]() \(\left\lbrack \begin{matrix}
m = 0 \\
m = - 4
\end{matrix} \right.\).
\(\left\lbrack \begin{matrix}
m = 0 \\
m = - 4
\end{matrix} \right.\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
----------------------------------
Qua chuyên đề xét tương giao dựa vào đồ thị của hàm số trị tuyệt đối, bạn không chỉ củng cố kiến thức về đồ thị và tính chất hàm số, mà còn học được cách nhận biết nhanh số nghiệm của phương trình thông qua hình học trực quan. Hy vọng bài viết này giúp bạn tự tin xử lý mọi dạng bài liên quan đến hàm trị tuyệt đối trong các đề thi THPT Quốc gia.










