Công thức tính nhanh khoảng cách (Tập 2)
Công thức tính nhanh khoảng cách (Tập 2)
Công thức tính nhanh khoảng cách (Tập 2) đưa ra công thức và hướng dẫn cách giải các dạng bài tập mở rộng về tìm khoảng cách trong hình học không gian. Hi vọng tài liệu này sẽ giúp các bạn ôn thi đại học môn Toán, luyện thi THPT Quốc gia môn Toán hiệu quả. Mời các bạn cùng tham khảo.
A.Tổng quan bài toán tính khoảng cách từ điểm đến mặt phẳng
Bài toán tổng quan. Cho hình chóp 
\(S.ABC\) có \(SA\) vuông góc mặt phẳng \((ABC)\), cho \(SA
= a,S_{\bigtriangleup ABC} = S\) và đường cao của tam giác ABC từ A là \(h = \frac{2S}{AB}\). Tính khoảng cách từ A đến mặt phẳng (SBC).
Hình vẽ minh họa
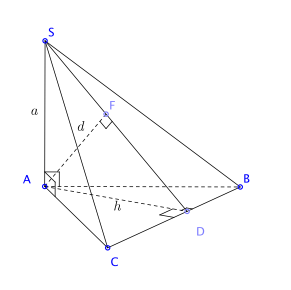
Gọi \(d\lbrack A,(SBC)\rbrack = d\). Khi đó: \(\frac{1}{d^{2}} = \frac{1}{a^{2}} +
\frac{1}{h^{2}}\)
Như vậy, việc tính khoảng cách đưa về tính đường cao của tam giác ABC và diện tích tam giác ABC được tính bằng công thức Herong. Chú ý là trong trường hợp này, tam giác ABC chi là tam giác thường.
B. Bài tập tự luận áp dụng tính khoảng cách từ điểm đến mặt phẳng
Bài toán 1. Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(SM\bot(ABCD)\) với M là trung điểm AB. Cho \(SA = a\sqrt{2},AB = 2a,BC = a\). Tính khoảng cách từ A đến \((SBD)\).
Hướng dẫn giải
Hình vẽ minh họa:
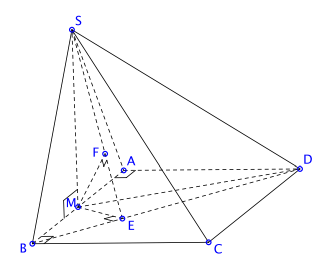
Ta tính \(d = d\lbrack
M,(SBD)\rbrack\).
Xét khối S.MBD. Đường cao
\(SM = \sqrt{SA^{2} - AM^{2}} =
\sqrt{2a^{2} - a^{2}} = a\)
Tính diện tích \(\bigtriangleup
MBD\) bằng công thức Herong.
Ta có: \(BM = a,BD = a\sqrt{5},MD =
a\sqrt{2}\).
Suy ra \(S_{MBD} =
\frac{1}{2}a^{2}\).
Khi đó: \(ME = \frac{2S_{MBD}}{BD} =
\frac{a^{2}}{a\sqrt{5}} = \frac{a}{\sqrt{5}}\).
Sau cùng, \(\frac{1}{d^{2}} =
\frac{1}{ME^{2}} + \frac{1}{SM^{2}} = \frac{5}{a^{2}} + \frac{1}{a^{2}}
= \frac{6}{a^{2}} \Rightarrow d = \frac{a}{\sqrt{6}}\).
Từ đó, \(d\lbrack A,(SBD)\rbrack = 2d =
\frac{2a}{\sqrt{6}}\).
Vậy khoảng cách từ A đến mặt phẳng SBD bằng \(\frac{2a}{\sqrt{6}}\).
Nhận xét. Qua ví dụ trên có thể thấy, việc tính khoảng cách từ một điểm bất kỳ sẽ được đưa về khoảng cách từ chân đường cao của hình chóp cần xét. Mặt khác, bước dụng hình chiếu sẽ được bó qua trong thực hành tính toán trắc nghiệm về sau. Ở ví dụ trên, việc tính ME sẽ đơn giản hơn với nhận xét ME bằng một nưa đường cao hạ từ A của tam giác vuông ABD. Tuy nhiên, để bạn đọc làm quen phương pháp cũng như có thuật toán giải quyết bài toán tông quát, chúng tôi vẫn làm theo cách lấy hai lần diện tích chia cạnh đáy.
Bài toán 2. Cho hình chóp \(S.ABCD\) có đáy ABCD là hình thoi tâm O canh a góc \(ABC = 60^{\circ}\), hình chiếu của S lên mặt phẳng \((ABCD)\) là điểm M nằm trên AC sao cho \(AC = 4AM\), góc tạo bời SC vói mặt đáy bằng \(60^{\circ}\). Tính khoảng cách từ A đến mặt (SBC).
Hướng dẫn giải
Hình vẽ minh họa:
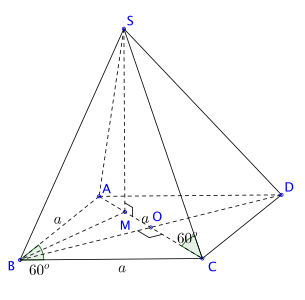
Ta tính d là khoảng cách từ M đến (SBC).
Xét khối chóp S.MBC.
Tam giác ABC đều nên dễ tính được \(MC =
\frac{3a}{4},BM = \frac{a\sqrt{13}}{4},SM =
\frac{3\sqrt{3}a}{4}\).
Gọi h là đường cao từ M cúa \(\bigtriangleup MBC\), khi đó, \(h \cdot BC = BO \cdot MC\)
Suy ra \(h = \frac{BO \cdot MC}{BC} =\dfrac{\dfrac{a\sqrt{3}}{2} \cdot \dfrac{3a}{4}}{a} =\dfrac{3a\sqrt{3}}{8}\).
Từ đó, \(\frac{1}{d^{2}} = \frac{1}{SM^{2}}
+ \frac{1}{h^{2}} = \frac{16}{27a^{2}} + \frac{64}{27a^{2}}\).
Suy ra: \(d =
\frac{3\sqrt{15}a}{20}\).
Và có được: \(d\lbrack A,(SBD)\rbrack =
\frac{4}{3}d = \frac{\sqrt{15}a}{5}\).
Vậy khoảng cách từ điểm A đến mặt phẳng SBD bằng \(\frac{\sqrt{15}a}{5}\).
C. Bài tập trắc nghiệm áp dụng tính khoảng cách từ điểm đến mặt phẳng
Câu 1: Khối tứ diện ABCD có AD vuông góc với mặt phẳng \((ABC).AC = 4,AD = 3cm,AB = 6cm\), \(BC = 5cm\). Khoảng cách từ B đến mặt phẳng \((ACD)\) là:
A. \(\frac{15\sqrt{7}}{4}cm\) B. \(\frac{15\sqrt{7}}{8}cm\) C. 3 cm D. \(\frac{3\sqrt{17}}{2}cm\)
Câu 2: Khối tứ diện ABCD có AD vuông góc với mặt phẳng \((ABC).AC = 4,AD = 3cm\), \(AB = 6cm,BC = 5cm\). Khoảng cách từ A đến mặt phẳng \((BCD)\) là:
A. \(\frac{3\sqrt{77}}{11}cm\) B. \(\frac{\sqrt{77}}{11}cm\) C. \(\frac{2\sqrt{77}}{11}cm\) D. 3 cm
Đáp án bài tập trắc nghiệm
Câu 1.
Hình vẽ minh họa:
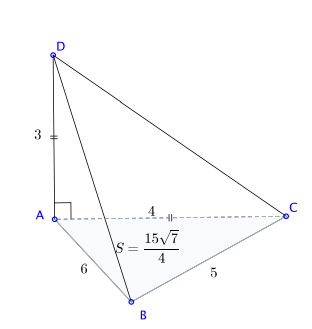
Tính được \(S_{ABC} =
\frac{15\sqrt{7}}{4}\).
Khoảng cách từ B đến \((ACD)\) sẽ là đường cao hạ từ B của tam giác ABC.
Ta có: \(h_{B} = \frac{2S_{ABC}}{AC} =
\frac{15\sqrt{7}}{8}\).
Câu 2.
Tính được \(S_{ABC} =
\frac{15\sqrt{7}}{4}\). Đường cao hạ từ A của tam giác ABC là:
\(h_{A} = \frac{2S_{ABC}}{BC} =
\frac{3\sqrt{7}}{2}.\)
Khi đó gọi d là khoảng cách từ A đến mặt phẳng \((BCD)\), ta có \(\frac{1}{d^{2}} = \frac{1}{h_{A}^{2}} +
\frac{1}{AD^{2}} = \frac{11}{63}\). Suy ra \(d = \frac{3\sqrt{77}}{11}\).
D. Bài tập tính khoảng cách giữa hai đường thẳng chéo nhau
Bài toán 1. Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại A, cạnh \(AB
= 2a,AC = a\). Hình chiếu của \(S\) lên mặt phẳng \((ABC)\) là trung điểm \(M\) của \(AB\). Góc giữa \(SC\) và đáy \((ABC)\) bằng \(60^{\circ}\). Tính khoảng cách giữa AB và SC.
Hướng dẫn giải
Hình vẽ minh họa:
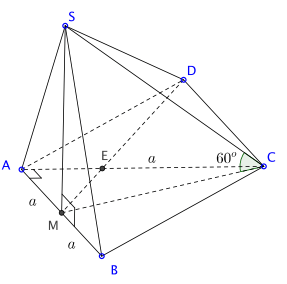
Dựng hình bình hành ABCD như hình vẽ. Khoảng cách AB và SC đưa về được khoảng cách từ M đến (SCD).
Ta xét khối chóp S.MCD.
Tính được, \(MC = a\sqrt{2},SM =MC\tan60^{\circ} = a\sqrt{6}\); gọi \(h_{M}\) lả đường cao từ M của tam giác MCD, \(h_{M} = AC = a\).
Gọi tiếp \(d = d\lbrack
M,(SCD)\rbrack\), ta có:
\(\frac{1}{d^{2}} = \frac{1}{h_{M}^{2}} +\frac{1}{SM^{2}} = \frac{1}{a^{2}} + \frac{1}{6a^{2}} =\frac{7}{6a^{2}}\)
Hay \(d = \frac{a\sqrt{42}}{7}\).
Vậy khoảng cách giữa AB và SC bằng \(\frac{a\sqrt{42}}{7}\).
Nhận xét. Do tính đặc biệt của hình trên, ta không cần tính diện tích tam giác MCD. Tuy nhiên trong trường hợp tổng quát, việc tính diện tích MCD và suy ra đường cao \(h_{M}\) sẽ là cần thiết để tính nhanh khoảng cách. Bạn đọc vui lòng thực hành lại phương pháp Herong tính diện tích tam giác MCD để kiểm tra lại đáp án.
---------------------------------------------------------------
Bài viết Công thức tính nhanh khoảng cách (Tập 2) tiếp nối nội dung ở tập trước, mang đến những kỹ thuật mở rộng và bài tập ứng dụng nâng cao giúp học sinh rèn luyện tư duy không gian và tăng tốc độ giải bài. Đây là tài liệu ôn thi Toán 12 quan trọng, hỗ trợ học sinh nắm chắc các công thức tính khoảng cách giữa điểm, đường thẳng và mặt phẳng, từ đó xử lý linh hoạt các câu hỏi vận dụng cao trong đề thi THPT Quốc gia.
Với cách trình bày logic, công thức tổng hợp khoa học và ví dụ minh họa sát thực tế, tài liệu này giúp bạn tối ưu chiến lược làm bài thi trắc nghiệm Toán, củng cố kiến thức hình học không gian và đạt hiệu quả học tập tốt nhất.
