Công thức tính nhanh khoảng cách (Tập 1)
Công thức tính nhanh khoảng cách (Tập 1)
Công thức tính nhanh khoảng cách (Tập 1) hướng dẫn các bạn giải các bài tập cơ bản về tìm khoảng cách trong hình học không gian. Hi vọng tài liệu này sẽ giúp các bạn ôn thi đại học môn Toán, luyện thi THPT Quốc gia môn Toán hiệu quả. Mời các bạn cùng tham khảo.
1. Công thức tính khoảng cách từ điểm đến mặt phẳng
Cho hình chóp O.ABC có OA, OB, OC đôi một vuông góc, cho OA = a, OB = b, OC = c. Tính khoảng cách từ O đến mặt phẳng (ABC).
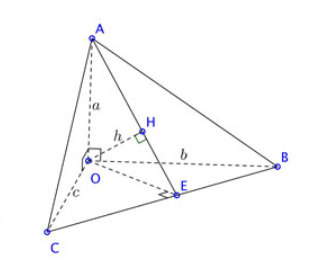
Gọi d là khoảng cách từ O đến mặt phẳng (ABC). Khi đó:
\(\frac{1}{{{d^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)
2. Bài tập áp dụng tính khoảng cách từ điểm đến mặt phẳng
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, \(BC = a\sqrt 2 ;SA = a\). Tính khoảng cách từ A đến (SBC).
Hướng dẫn giải
Hình vẽ minh họa:
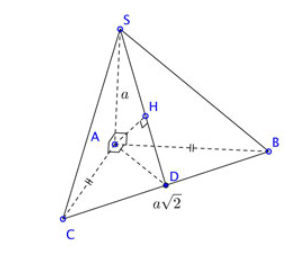
Ta có:
\(\dfrac{1}{{{d^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} + \dfrac{1}{{S{A^2}}}\)
\(= \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{3}{{{a^2}}}\)
\(\Rightarrow {d_A} = \dfrac{{a\sqrt 3 }}{3}\)
Vậy khoảng cách từ điểm A đến (SBC) bằng \(\dfrac{{a\sqrt 3 }}{3}\).
Bài 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh có độ dài a. Tính khoảng cách từ A đến mặt (SBC)
Hướng dẫn giải
Hình vẽ minh họa:
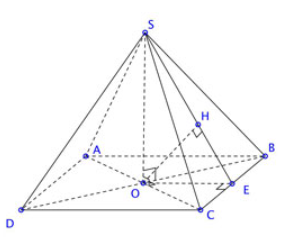
Xét hình chóp S.OBC ta có:
\(\dfrac{1}{{{d^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{S{O^2}}}\)
\(= \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}}}\)
\(\Rightarrow {d_O} = \dfrac{{a\sqrt 6 }}{6}\)
Từ đó suy ra \(\Rightarrow {d_A} = 2{d_O} = \frac{{a\sqrt 6 }}{3}\)
Vậy khoảng cách từ điểm A đến (SBC) bằng \(\dfrac{{a\sqrt 6 }}{3}\).
Bài 3. Cho hình nón có đường sinh 5cm, đường tròn đáy có chu vi bằng \(8\pi \left( {cm} \right)\), mặt phẳng (P) qua đỉnh S cắt đường tròn đáy tại 2 điểm A, B thỏa mãn \(AB = 4\sqrt 2\). Tính khoảng cách từ tâm O của đường tròn đáy đến mặt phẳng (P).
Hướng dẫn giải
Hình vẽ minh họa:
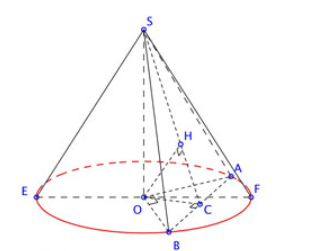
Vì tam giác OAB có \(AB = OA\sqrt 2\)
Suy ra tam giác OAB vuông cân tại O; \(SO = \sqrt {S{A^2} - A{O^2}} =3\)
Ta có:
\(\dfrac{1}{{{d_O}^2}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{S{O^2}}}\)
\(= \dfrac{1}{{{4^2}}} + \dfrac{1}{{{4^2}}} + \dfrac{1}{{{3^2}}} = \dfrac{{17}}{{27}}\)
\(\Rightarrow {d_O} = \dfrac{{6\sqrt {34} }}{{17}}\).
Vậy khoảng cách từ tâm O của đường tròn đáy đến mặt phẳng (P) bằng \(\dfrac{{6\sqrt {34} }}{{17}}\).
Bài 4. Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A. Biết AB = a; AC = 2a; AA' = 3a. Gọi M, N lần lượt là BB'; CC'.
a. Tính khoảng cách từ A đến (A'MN).
b. Tính khoảng cách từ B' đến (A'MN).
Hướng dẫn giải
Hình vẽ minh họa:
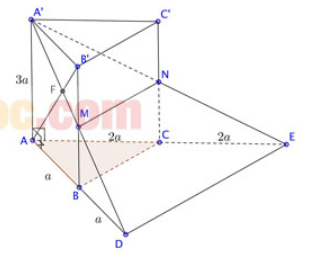
a. Kéo dài A'N và A'M cắt AC, AB lần lượt tại E và D (như hình vẽ). Khi đó:
\(d = d\left[ {A;\left( {A'MN} \right)} \right] = d\left[ {A;\left( {A'DE} \right)} \right]\)
Ta có:
\(\dfrac{1}{{{d^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{A{E^2}}} + \dfrac{1}{{AA{'^2}}}\)
\(= \dfrac{1}{{{{\left( {2a} \right)}^2}}} + \dfrac{1}{{{{\left( {4a} \right)}^2}}} + \dfrac{1}{{{{\left( {3a} \right)}^2}}} = \dfrac{{61}}{{144{a^2}}}\)
\(\Rightarrow d = \dfrac{{12\sqrt {61} }}{{61}} a\)
b. Gọi F là giao điểm của AB' và A'D, suy ra \(B'F = \frac{1}{2}AF\)
Khi đó: \(d\left[ {B;\left( {A'MN} \right)} \right] = \frac{1}{2}d\left[ {A;\left( {A'MN} \right)} \right] = \frac{{6\sqrt {61} }}{{61}}a\)
-------------------------------------------------------------
Bài viết Công thức tính nhanh khoảng cách (Tập 1) không chỉ hệ thống hóa những công thức tính khoảng cách trong không gian và mặt phẳng thường gặp, mà còn cung cấp phương pháp giải nhanh – chính xác, giúp học sinh tiết kiệm thời gian khi làm bài trắc nghiệm. Tài liệu này phù hợp cho học sinh lớp 12 ôn thi THPT Quốc gia môn Toán, cũng như giáo viên muốn tham khảo để ra đề hoặc hướng dẫn học sinh luyện tập.
Việc nắm vững và áp dụng linh hoạt các công thức tính nhanh khoảng cách sẽ giúp bạn chinh phục dễ dàng các dạng bài tập hình học không gian – một phần quan trọng trong cấu trúc đề thi. Hãy lưu lại và tiếp tục theo dõi Tập 2 để hoàn thiện kỹ năng giải Toán nhanh – hiệu quả, đạt điểm cao trong kỳ thi sắp tới.
