Điều kiện để hàm trùng phương có cực đại và cực tiểu
Chuyên đề Toán 12: Cực trị của hàm trùng phương
Trong chương trình Toán 12, phần cực trị của hàm số trùng phương là dạng bài quan trọng giúp học sinh nắm vững bản chất của đạo hàm bậc nhất và bậc hai, từ đó xác định được cực đại – cực tiểu của hàm. Việc hiểu rõ điều kiện để hàm trùng phương có cực đại và cực tiểu không chỉ giúp giải nhanh các bài tập trắc nghiệm, mà còn là nền tảng cho các dạng toán khảo sát và ứng dụng đồ thị.
Bài viết này sẽ hướng dẫn chi tiết cách xác định điều kiện có cực trị của hàm trùng phương, kèm theo ví dụ minh họa, lời giải chi tiết và đáp án chuẩn, giúp học sinh ôn thi THPT Quốc gia môn Toán hiệu quả và tự tin đạt điểm cao.
A. Cách xác định cực trị hàm trùng phương
Xác định điều kiện để hàm số 
\(y = ax^{4} +
bx^{2} + c\) có cực trị:
- Hàm số: \(y = ax^{4} + bx^{2} + c\). Hệ số \(a\) có thể bằng \(0\).
- Hàm số có \(3\) cực trị \(\Rightarrow ab < 0\)
- Hàm số có 1 cực trị \(\Rightarrow ab \geq 0\).
Có \(4\) trường hợp sau có thể xảy ra:
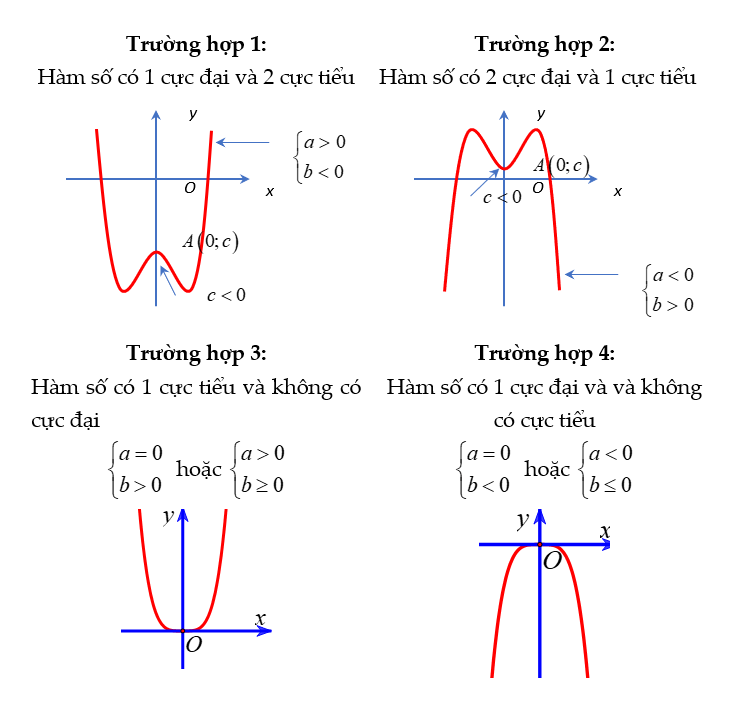
Lưu ý: Trường hợp \(3\) và \(4\) khi hệ số \(a
= 0\) đồ thị hàm số sẽ là parabol \(y =
bx^{2} + c\), đồ thị hàm số sẽ có \(1\) điểm cực trị.
B. Ví dụ minh họa điều kiện để hàm trùng phương có cực trị
Ví dụ 1. Tìm tất cả các giá trị của tham số \(m\) để hàm số sau có cực trị \(y = x^{4} - 2(m + 1)x^{2} + m\).
A. \(m < - 1\). B. \(\mathbb{R}\). C. \(m \neq - 1\). D. \(m > - 1\).
Hướng dẫn giải
Chọn B
Nếu \(ab < 0\) thì hàm số có ba cực trị.
Nếu \(ab \geq 0\) thì hàm số có 1 cực trị.
Vậy hàm số \(y = ax^{4} + bx^{2} + c,(a
\neq 0)\) luôn có cực trị với mọi số thực \(a,b,c\).
Ví dụ 2. Cho hàm số \(y = ax^{4} + bx^{2} +
1\ (a \neq 0).\) Để hàm số có một cực tiểu và hai cực đại thì \(a,b\) cần thoả mãn:
A. \(a < 0,b < 0.\) B. \(a > 0,b < 0.\) C. \(a < 0,b > 0.\) D. \(a > 0,b > 0.\)
Hướng dẫn giải
Chọn B.
Ta có \(y' = 4ax^{3} + 2bx = 2x\left(ax^{2} + b \right);y' = 0\)
\(\Leftrightarrow \left\lbrack\begin{matrix}x = 0 \\x^{2} = - \dfrac{b}{2a}\end{matrix} \right.\)
Để hàm số có một cực tiểu và hai cực đại \(\left\{ \begin{matrix}
a < 0 \\
- \frac{b}{2a} > 0
\end{matrix} \right.\ .\)
Ví dụ 3. Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y
= (m - 1)x^{4} - 2(m - 3)x^{2} + 1\) không có cực đại?
A. \(1 \leq m \leq 3\) B. \(m \leq 1\) C. \(m \geq 1\) D. \(1 < m \leq 3\)
Hướng dẫn giải
Chọn A
TH1: Nếu \(m = 1 \Rightarrow y = 4x^{2} +
1\). Suy ra hàm số không có cực đại.
TH2: Nếu \(m > 1\).
Để hàm số không có cực đại thì \(- 2(m - 3)
\geq 0 \Leftrightarrow m \leq 3\).
Suy ra \(1 < m \leq 3\).
Vậy \(1 \leq m \leq 3\).
Ví dụ 4. Cho hàm số \(y = ax^{4} + bx^{2} +
c\ (a \neq 0).\) Trong điều kiện nào sau đây thì hàm số có ba cực trị:
A. \(a,b\) cùng dấu và \(c\) bất kì. B. \(a,b\) trái dấu và \(c\) bất kì.
C. \(b = 0\) và \(a,c\) bất kì. D. \(c = 0\) và \(a,b\) bất kì.
Hướng dẫn giải
Chọn B.
Ta có:
\(y' = 4ax^{3} + 2bx = 2x\left(2ax^{2} + b \right);y' = 0\)
\(\Leftrightarrow \left\lbrack\begin{matrix}x = 0 \\x^{2} = - \frac{b}{a}\end{matrix} \right.\ .\)
Để hàm số có ba cực trị thì phương trình \(x^{2} = - \frac{b}{2a}\) phải có hai nghiệm phân biệt khác \(0.\) Vậy \(- \frac{b}{2a} > 0.\)
Khi đó \(a,b\) trái dấu và \(c\) bất kì.
C. Bài tập tự rèn luyện cực trị hàm trùng phương có đáp án chi tiết
Bài tập 1. Để đồ thị hàm số \(y = - x^{4} -
(m - 3)x^{2} + m + 1\) có điểm cực đại mà không có điểm cực tiểu thì tất cả giá trị thực của tham số \(m\) là:
A. \(m \geq 3\). B. \(m > 3\). C. \(m \leq 3\). D. \(m < 3\).
Bài tập 2. Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y
= (m - 1)x^{4} + mx^{2} + 1\) có đúng một điểm cực tiểu.
A. \(m \in \lbrack 0;1\rbrack\). B. \(m \in \lbrack 1; + \infty)\). C. \(m \in (0; + \infty)\). D. \(m \in (0;1) \cup (1; + \infty)\).
Bài tập 3. Gọi \(A\), \(B\), \(C\) là \(3\) điểm cực trị của đồ thị hàm số \(y = 2x^{4} - 4x^{2} + 1\). Diện tích của tam giác \(ABC\) là:
A. \(3\). B. \(1\). C. \(4\). D. \(2\)
Bài tập 4. Tìm \(m\) để đồ thị hàm số \(y = x^{4} - 2mx^{2} + 1\) có ba điểm cực trị \(A(0;\ 1),\ B,\ C\) thỏa mãn \(BC = 4?\)?
A. \(m = \sqrt{2}\). B. \(m = 4\). C. \(m =
\pm 4\). D. \(m = \pm
\sqrt{2}\).
Bài tập 5. Tìm tất cả các giá trị thực của tham số \(m\) để đồ thị của hàm số \(y = x^{4} - 2mx^{2}\) có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn \(1\).
A. \(0 < m < \sqrt[3]{4}\) B. \(m < 1\) C. \(0 < m < 1\) D. \(m > 0\)
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
--------------------------------------------------------------
Qua bài viết Điều kiện để hàm trùng phương có cực đại và cực tiểu, bạn đã nắm được cách nhận biết và xác định cực trị của hàm trùng phương bằng phương pháp đạo hàm cùng các dấu hiệu cực đại – cực tiểu đặc trưng. Hãy luyện tập thêm các bài tập cực trị hàm trùng phương có đáp án chi tiết để củng cố kiến thức, rèn luyện kỹ năng và tự tin chinh phục mọi dạng đề Toán 12.
