Khảo sát hàm số giá trị tuyệt đối Toán 12: Bài tập và đáp án
Chuyên đề hàm số giá trị tuyệt đối Toán 12
Trong chương trình Toán 12, dạng bài khảo sát hàm số giá trị tuyệt đối là một chuyên đề quan trọng, đòi hỏi học sinh phải nắm vững cả kiến thức đạo hàm, bảng biến thiên và kỹ năng vẽ đồ thị. Đây cũng là dạng bài thường xuất hiện trong đề thi THPT Quốc gia môn Toán, giúp đánh giá khả năng phân tích và tư duy hình học của học sinh.
Bài viết này sẽ hướng dẫn chi tiết cách khảo sát hàm số giá trị tuyệt đối Toán 12, đồng thời cung cấp bài tập kèm đáp án chi tiết giúp bạn luyện tập hiệu quả, củng cố kiến thức và tự tin chinh phục điểm cao trong kỳ thi sắp tới.
A. Ví dụ minh họa khảo sát hàm số chứa dấu giá trị tuyệt đối
Bài tập 1. Hàm số ![]() \(y = f(x)\) có đồ thị như hình vẽ bên.
\(y = f(x)\) có đồ thị như hình vẽ bên.
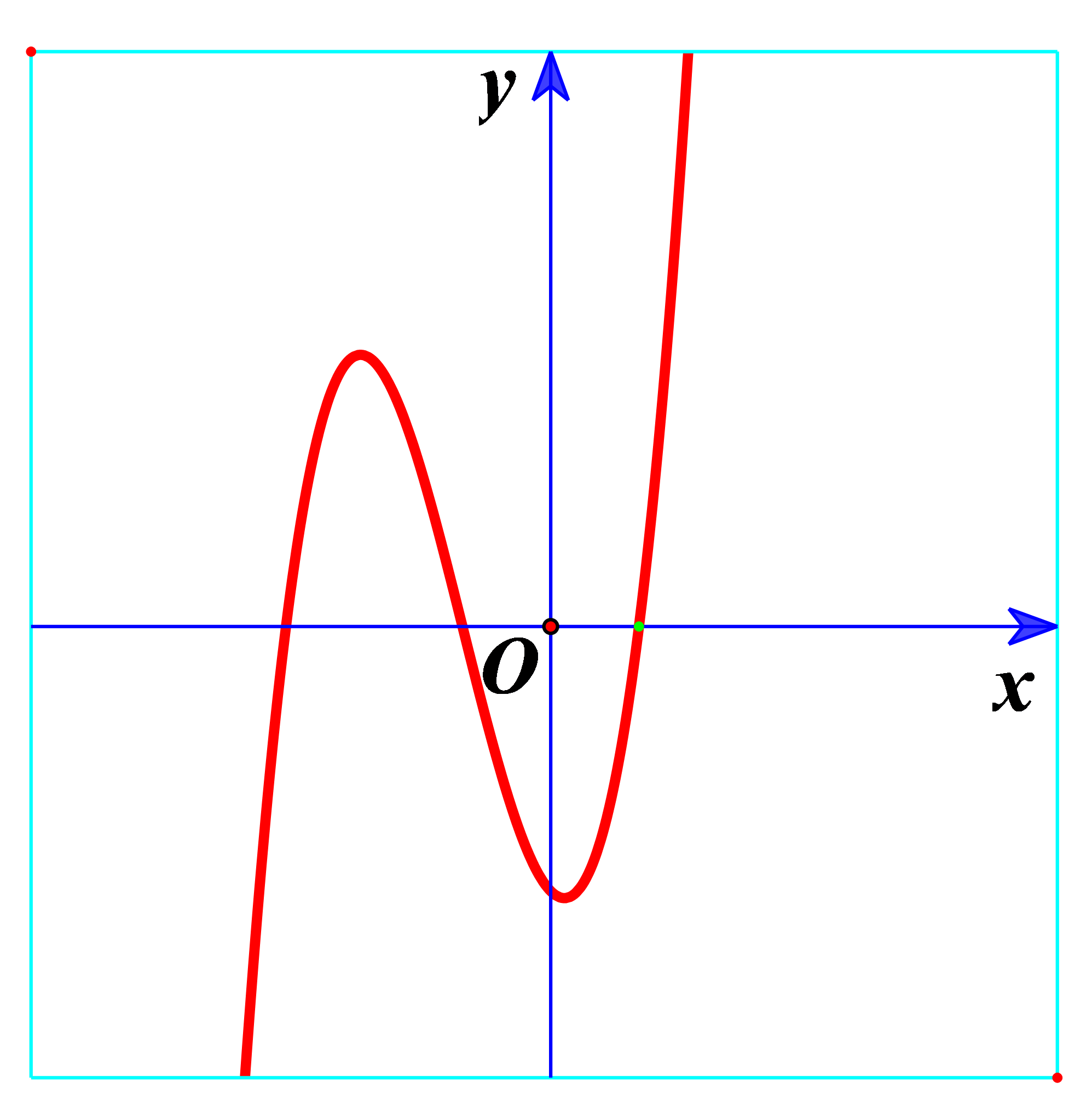
Hình nào dưới đây là đồ thị của hàm số ![]() \(y
= \left| f(x) \right|\)?
\(y
= \left| f(x) \right|\)?
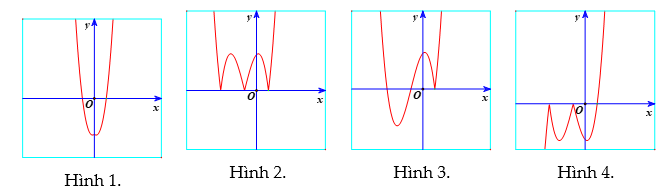
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Hướng dẫn giải
Chọn B
Đây là dạng bài từ đồ thị ![]() \((C):y =
f(x)\), suy ra đồ thị
\((C):y =
f(x)\), suy ra đồ thị  \((C'):y =
\left| f(x) \right|\).
\((C'):y =
\left| f(x) \right|\).
Đồ thị hàm số ![]() \(y = \left| f(x)
\right|\) bao gồm:
\(y = \left| f(x)
\right|\) bao gồm:
+ Phần đồ thị hàm số ![]() \(y = f(x)\) nằm phía trên
\(y = f(x)\) nằm phía trên ![]() \(Ox\) (cả những điểm nằm trên
\(Ox\) (cả những điểm nằm trên ![]() \(Ox\)).
\(Ox\)).
+ Phần đối xứng với phần đồ thị hàm số ![]() \(y
= f(x)\)nằm phía dưới
\(y
= f(x)\)nằm phía dưới ![]() \(Ox\)qua
\(Ox\)qua ![]() \(Ox\).
\(Ox\).
Khi đó, ta được đồ thị như hình vẽ:
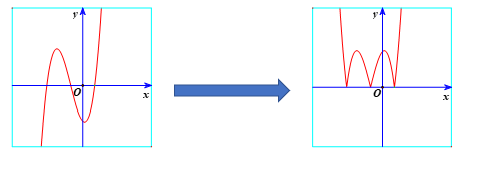
Nhận xét: Đồ thị hàm số ![]() \(y = \left| f(x)
\right|\) luôn nằm trên trục
\(y = \left| f(x)
\right|\) luôn nằm trên trục ![]() \(Ox\)nên có thể loại ngay các đáp án A. C. D.
\(Ox\)nên có thể loại ngay các đáp án A. C. D.
Ví dụ 2. Hàm số ![]() \(y = \frac{x - 2}{x +
1}\) có đồ thị như hình vẽ bên.
\(y = \frac{x - 2}{x +
1}\) có đồ thị như hình vẽ bên.
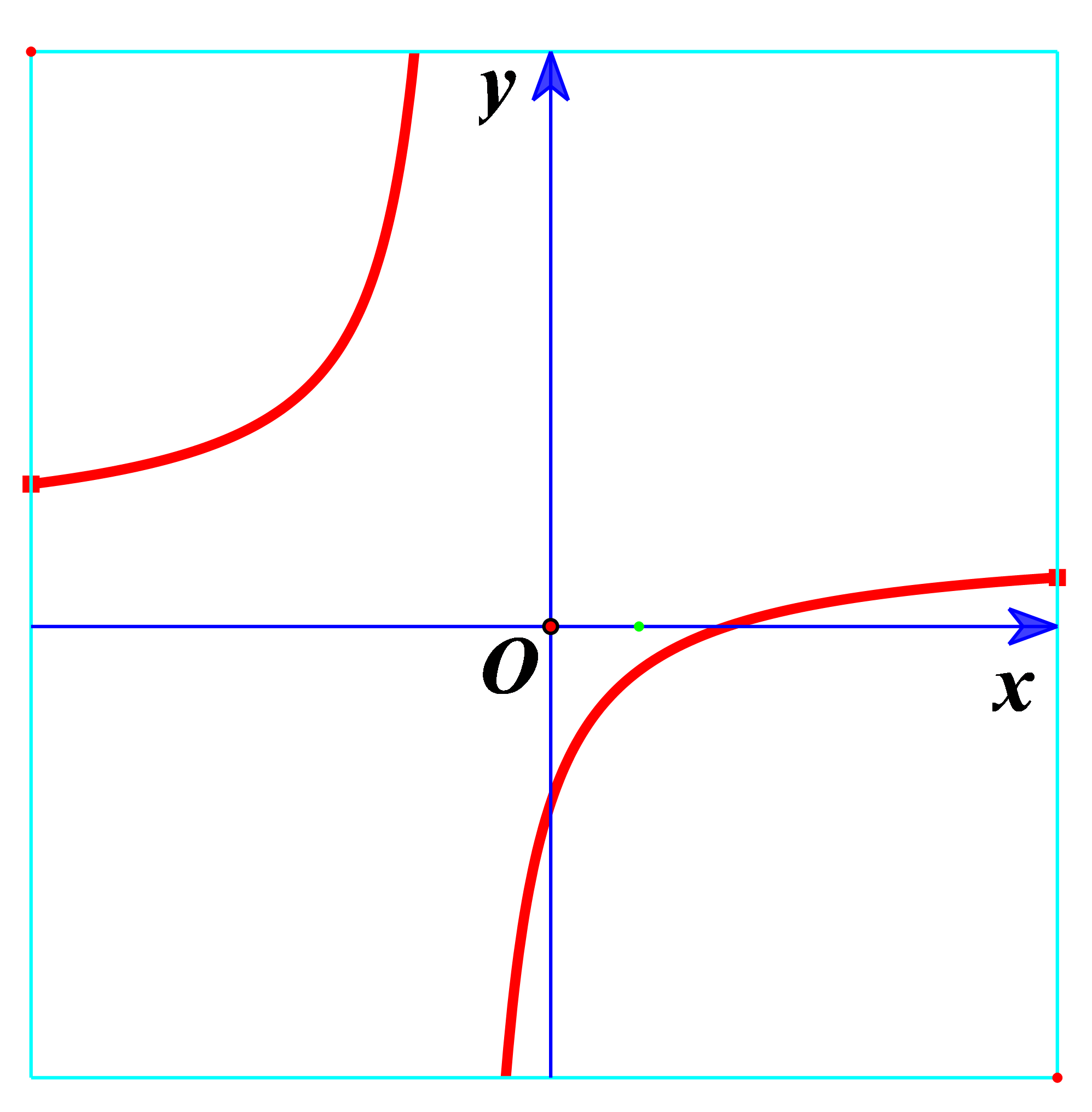
Hình nào dưới đây là đồ thị của hàm số ![]() \(y = \left| \frac{x - 2}{x + 1}
\right|\)?
\(y = \left| \frac{x - 2}{x + 1}
\right|\)?
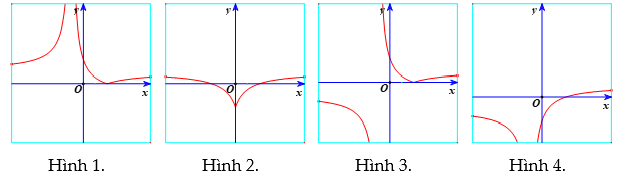
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Hướng dẫn giải
Chọn A
Đây là dạng bài từ đồ thị ![]() \((C):y =
f(x)\), suy ra đồ thị
\((C):y =
f(x)\), suy ra đồ thị  \((C'):y =
\left| f(x) \right|\).
\((C'):y =
\left| f(x) \right|\).
Đồ thị hàm số ![]() \(y = \left| \frac{x - 2}{x +
1} \right|\) bao gồm:
\(y = \left| \frac{x - 2}{x +
1} \right|\) bao gồm:
+ Phần đồ thị hàm số ![]() \(y = \frac{x - 2}{x +
1}\)nằm phía trên
\(y = \frac{x - 2}{x +
1}\)nằm phía trên ![]() \(Ox\) (cả những điểm nằm trên
\(Ox\) (cả những điểm nằm trên ![]() \(Ox\)).
\(Ox\)).
+ Phần đối xứng với phần đồ thị hàm số ![]() \(y
= \frac{x - 2}{x + 1}\)nằm phía dưới
\(y
= \frac{x - 2}{x + 1}\)nằm phía dưới ![]() \(Ox\)qua
\(Ox\)qua ![]() \(Ox\).
\(Ox\).
Khi đó, ta được đồ thị như hình vẽ:
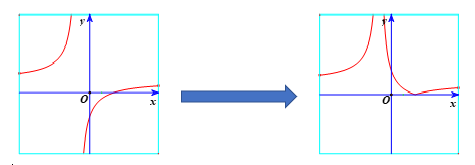
Nhận xét: Đồ thị hàm số ![]() \(y = \left| f(x)
\right|\) luôn nằm trên trục
\(y = \left| f(x)
\right|\) luôn nằm trên trục ![]() \(Ox\)nên có thể loại ngay các đáp án B. C. D.
\(Ox\)nên có thể loại ngay các đáp án B. C. D.
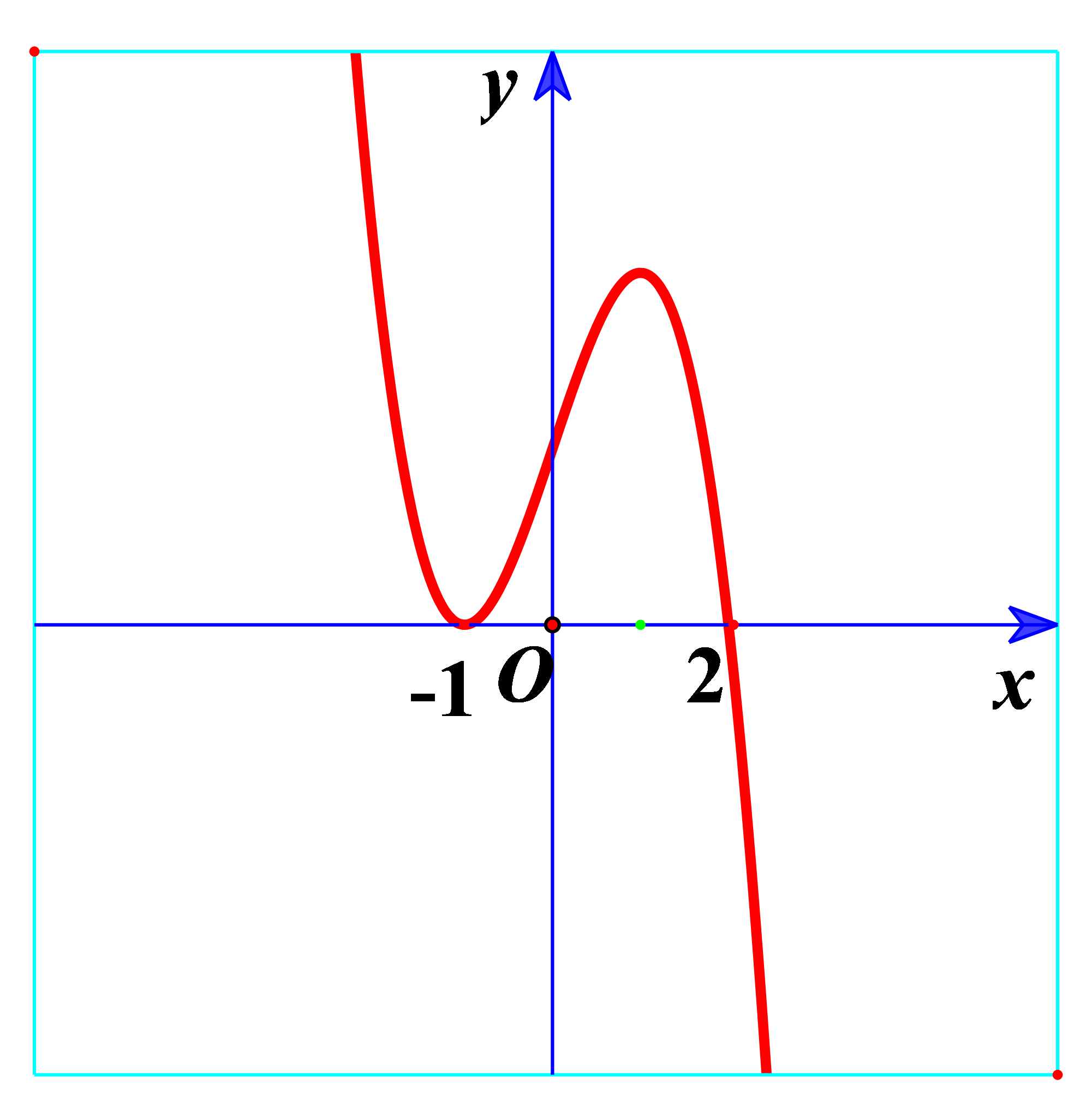
Ví dụ 3. Hàm số ![]() \(y = 2 + 3x -
x^{3}\) có đồ thị như hình vẽ bên.
\(y = 2 + 3x -
x^{3}\) có đồ thị như hình vẽ bên.
Hình nào dưới đây là đồ thị của hàm số ![]() \(y = 2 + 3|x| -
|x|^{3}\)?
\(y = 2 + 3|x| -
|x|^{3}\)?
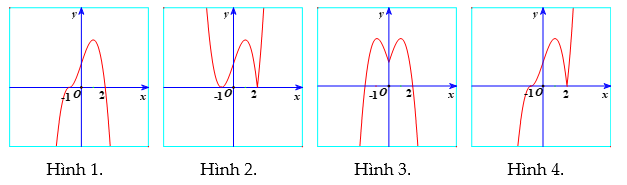
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Hướng dẫn giải
Chọn C
Đây là dạng bài từ đồ thị ![]() \((C):y =
f(x)\), suy ra đồ thị
\((C):y =
f(x)\), suy ra đồ thị  \((C'):y =
f\left( |x| \right)\).
\((C'):y =
f\left( |x| \right)\).
Đồ thị hàm số ![]() \(y = 2 + 3|x| -
|x|^{3}\) bao gồm:
\(y = 2 + 3|x| -
|x|^{3}\) bao gồm:
+ Phần đồ thị hàm số ![]() \(y = 2 + 3x -
x^{3}\)nằm bên phải
\(y = 2 + 3x -
x^{3}\)nằm bên phải ![]() \(Oy\) (cả những điểm nằm trên
\(Oy\) (cả những điểm nằm trên ![]() \(Oy\)).
\(Oy\)).
+ Phần đối xứng với phần đồ thị hàm số ![]() \(y
= 2 + 3x - x^{3}\) nằm bên phải
\(y
= 2 + 3x - x^{3}\) nằm bên phải ![]() \(Oy\) qua
\(Oy\) qua ![]() \(Oy\).
\(Oy\).
Khi đó, ta được đồ thị như hình vẽ:
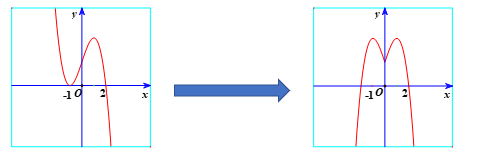
Nhận xét: Đồ thị hàm số ![]() \(y = f\left( |x|
\right)\)nhận trục
\(y = f\left( |x|
\right)\)nhận trục ![]() \(Oy\) làm trục đối xứng nên có thể loại ngay các đáp án A. B. D.
\(Oy\) làm trục đối xứng nên có thể loại ngay các đáp án A. B. D.
Ví dụ 4. Hàm số ![]() \(y = \frac{1 - x}{x +
1}\) có đồ thị như hình vẽ bên.
\(y = \frac{1 - x}{x +
1}\) có đồ thị như hình vẽ bên.
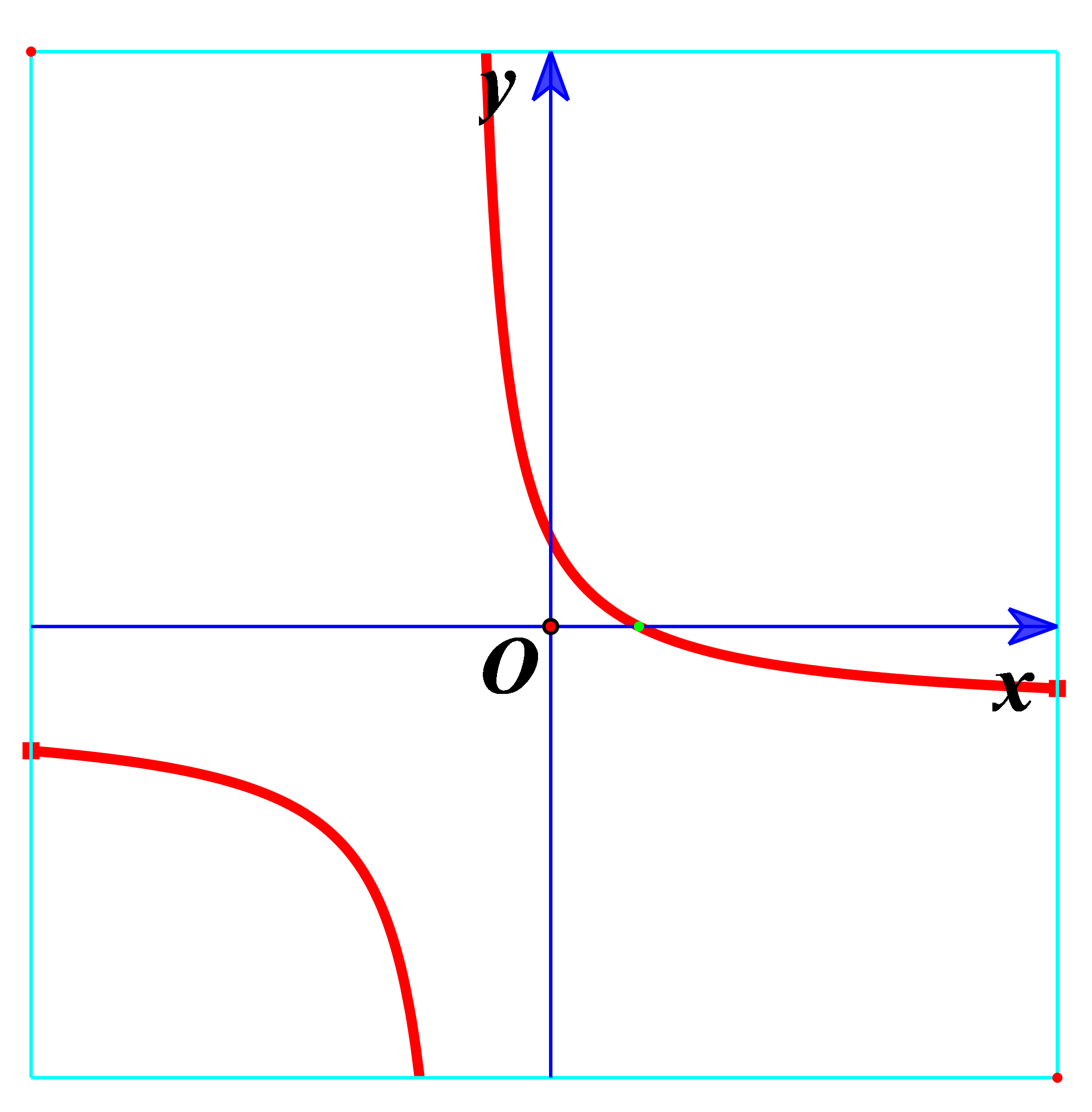
Hình nào dưới đây là đồ thị của hàm số ![]() \(y = \frac{1 - |x|}{|x| +
1}\)?
\(y = \frac{1 - |x|}{|x| +
1}\)?
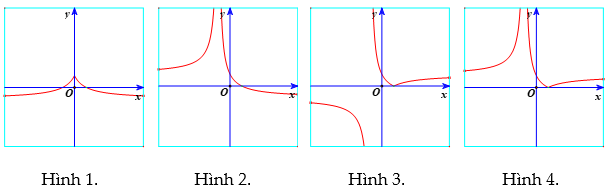
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Hướng dẫn giải
Chọn A
Đây là dạng bài từ đồ thị ![]() \((C):y =
f(x)\), suy ra đồ thị
\((C):y =
f(x)\), suy ra đồ thị  \((C'):y =
f\left( |x| \right)\).
\((C'):y =
f\left( |x| \right)\).
Đồ thị hàm số ![]() \(y = \frac{1 - |x|}{|x| +
1}\) bao gồm:
\(y = \frac{1 - |x|}{|x| +
1}\) bao gồm:
+ Phần đồ thị hàm số ![]() \(y = \frac{1 - x}{x +
1}\)nằm bên phải
\(y = \frac{1 - x}{x +
1}\)nằm bên phải ![]() \(Oy\) (cả những điểm nằm trên
\(Oy\) (cả những điểm nằm trên ![]() \(Oy\)).
\(Oy\)).
+ Phần đối xứng với phần đồ thị hàm số ![]() \(y
= \frac{1 - x}{x + 1}\) nằm bên phải
\(y
= \frac{1 - x}{x + 1}\) nằm bên phải ![]() \(Oy\) qua
\(Oy\) qua ![]() \(Oy\).
\(Oy\).
Khi đó, ta được đồ thị như hình vẽ:
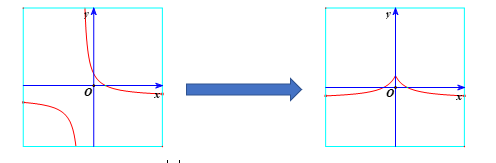
Nhận xét: Đồ thị hàm số ![]() \(y = \frac{1 -
|x|}{|x| + 1}\)nhận trục
\(y = \frac{1 -
|x|}{|x| + 1}\)nhận trục ![]() \(Oy\) làm trục đối xứng nên có thể loại ngay các đáp án B. C. D.
\(Oy\) làm trục đối xứng nên có thể loại ngay các đáp án B. C. D.
B. Bài tập tự rèn luyện khảo sát hàm số chứa dấu giá trị tuyệt đối có đáp án
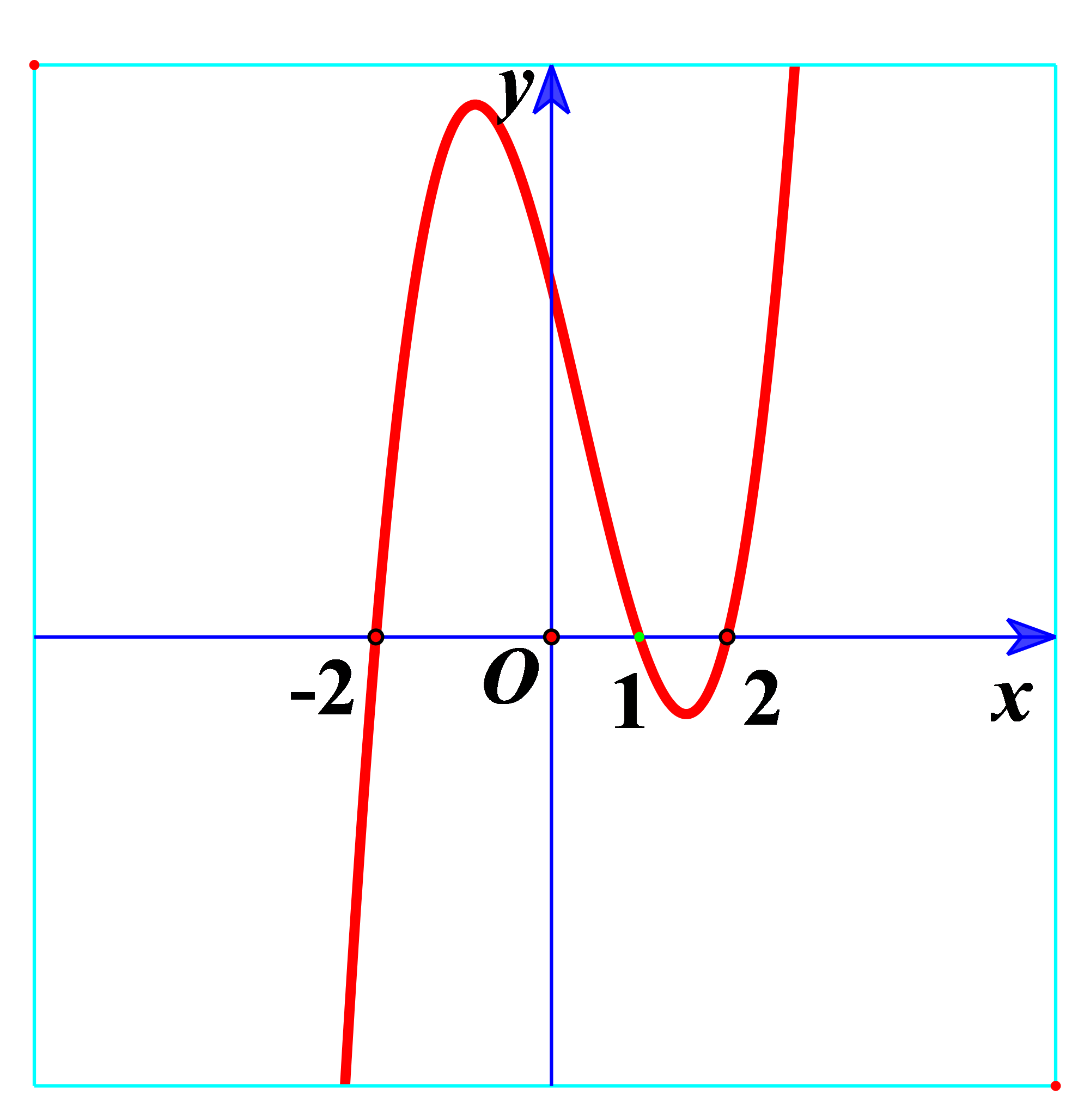
Bài tập 1. Hàm số ![]() \(y = (x - 1)\left( x^{2}
- 4 \right)\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số
\(y = (x - 1)\left( x^{2}
- 4 \right)\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số ![]() \(y = |x - 1|\left( x^{2} - 4
\right)\)?
\(y = |x - 1|\left( x^{2} - 4
\right)\)?
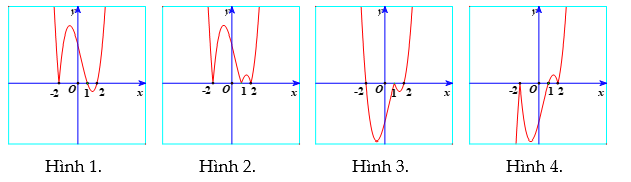
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
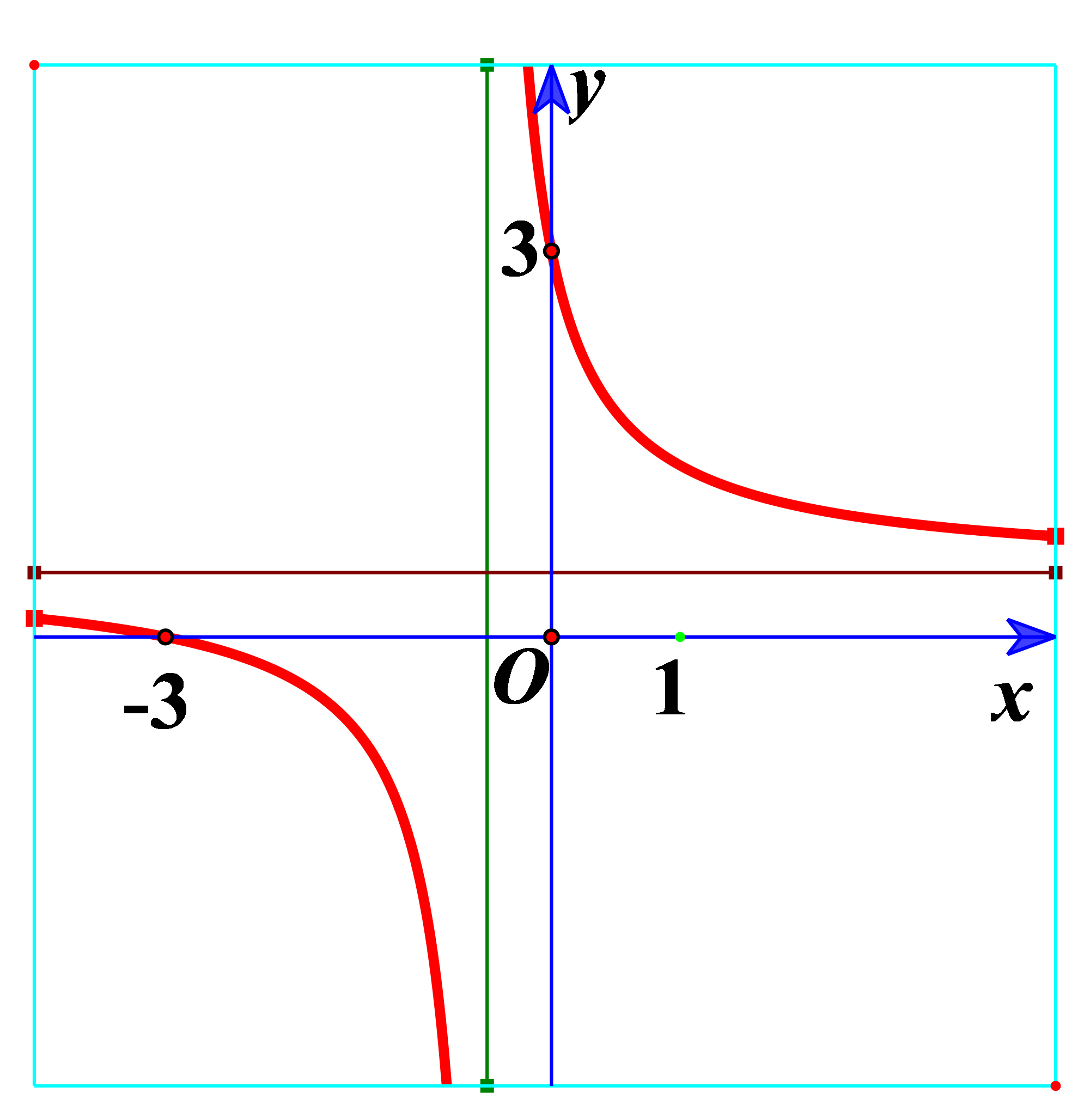
Bài tập 2. Hàm số ![]() \(y = \frac{x + 3}{2x +
1}\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số
\(y = \frac{x + 3}{2x +
1}\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số ![]() \(y = \frac{|x + 3|}{2x +
1}\)?
\(y = \frac{|x + 3|}{2x +
1}\)?
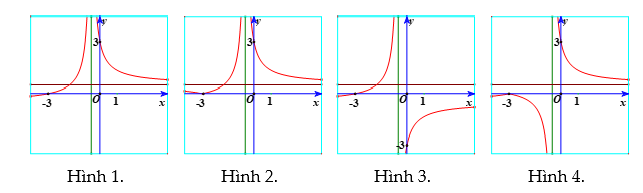
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Bài tập 3. Hàm số ![]() \(y = \frac{x - 5}{1 -
x}\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số
\(y = \frac{x - 5}{1 -
x}\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số ![]() \(y = \frac{x - 5}{|1 -
x|}\)?
\(y = \frac{x - 5}{|1 -
x|}\)?
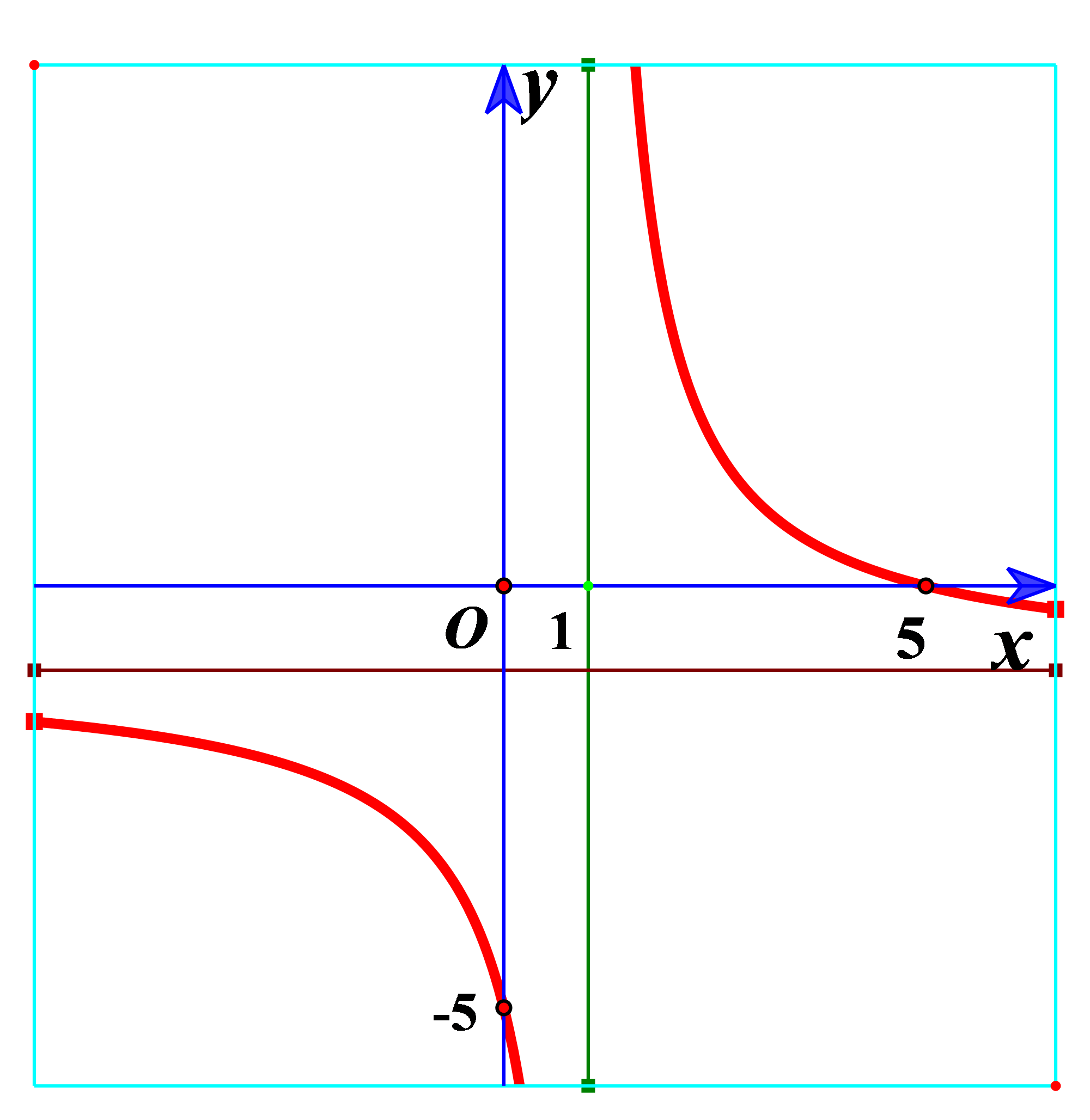
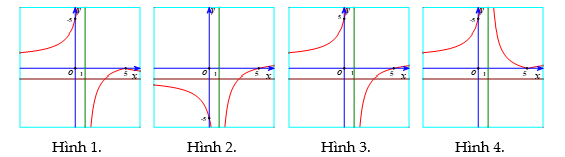
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4
Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.
----------------------------------------------------------
Qua bài viết Khảo sát hàm số giá trị tuyệt đối Toán 12: Bài tập và đáp án, bạn đã được hệ thống đầy đủ các bước khảo sát, phân tích đồ thị và giải chi tiết các dạng bài tập thường gặp.
Hãy thường xuyên ôn luyện và thực hành với các dạng bài giá trị tuyệt đối có đáp án, kết hợp cùng các chuyên đề hàm số, đạo hàm và cực trị, để nâng cao kỹ năng và đạt kết quả tốt nhất trong kỳ thi THPT Quốc gia môn Toán.










