Lý thuyết và bài tập hình học OXY (có lời giải chi tiết)
Hệ thống kiến thức cơ bản hình học OXY
Để học tốt môn Toán lớp 12: Hình học OXY các bạn học sinh cần nắm chắc lý thuyết và rèn luyện cách giải bài tập một cách nhanh và chính xác. VnDoc.com đã tổng hợp những kiến thức cơ bản qua bộ tài liệu: Lý thuyết và bài tập hình học OXY (có lời giải chi tiết), mời các bạn và thầy cô tham khảo.
Câu hỏi trắc nghiệm có đáp án môn Toán lớp 12: Nguyên hàm - tích phân
Lý thuyết và bài tập hình học OXY (có lời giải chi tiết)
PHẦN I: CÁC CÔNG THỨC CƠ BẢN
Xét hệ trục tọa độ Oxy với Ox là trục hoành nằm ngang với vectơ đơn vị là 
\(\overrightarrow{i}\), Oy là trục tung vectơ đơn vị là \(\overrightarrow{j}\), Oy vuông góc với Ox tại gốc tọa độ O, ta có các công thức được sử dụng sau:
Công thức độ dài:
Nếu có hai điểm \(A\left( x_{A};y_{A}
\right),B\left( x_{B};y_{B} \right)\) thì độ dài đoạn thẳng AB được tính theo công thức \(AB = \sqrt{\left(
x_{B} - x_{A} \right)^{2} + \left( y_{B} - y_{A}
\right)^{2}}\)
Công thức tính tọa độ vectơ:
Nếu có hai điểm \(A\left( x_{A};y_{A}
\right),B\left( x_{B};y_{B} \right)\) thì \(\overrightarrow{AB} = \left( x_{B} - x_{A};y_{B} -
y_{A} \right)\)
Phép cộng và trừ hai vectơ:
Nếu có \(\overrightarrow{a} = \left(
a_{1};a_{2} \right),\overrightarrow{b} = \left( b_{1};b_{2}
\right)\) thì \(\overrightarrow{a} \pm
\overrightarrow{b} = \left( a_{1} \pm a_{2};b_{1} \pm b_{2}
\right)\)
Hai vectơ bằng nhau: là hai vectơ dài bằng nhau, cùng phương, cùng hướng.
Nếu có \(\overrightarrow{a} = \left(
a_{1};a_{2} \right),\overrightarrow{b} = \left( b_{1};b_{2}
\right)\) thì \(\overrightarrow{a} =
\overrightarrow{b} \Leftrightarrow \left\{ \begin{matrix}
a_{1} = b_{1} \\
a_{2} = b_{2} \\
\end{matrix} \right.\)(hoành bằng hoành, tung bằng tung)
Tích một số và một vectơ:
Cho vectơ \(\overrightarrow{a}\)khi đó \(k\overrightarrow{a}\) với k là số thực khác 0:
- Nếu \(k > 0:k\overrightarrow{a}\) là vectơ dài gấp k lần vectơ \(\overrightarrow{a}\) và cùng hướng với \(\overrightarrow{a}\).
- Nếu \(k < 0:k\overrightarrow{a}\) là vectơ dài gấp k lần vectơ \(\overrightarrow{a}\) và ngược hướng với \(\overrightarrow{a}\).
- Về mặt tọa độ: nếu \(\overrightarrow{a} =
\left( a_{1};a_{2} \right)\)thì \(k\overrightarrow{a} = \left( ka_{1};ka_{2}
\right)\)
Tích vô hướng của hai vectơ:
Định nghĩa.
Người ta gọi tích số \(\left|
\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|.cos\left(
\overrightarrow{a};\overrightarrow{b} \right)\) là tích vô hướng của hai vectơ \(\overrightarrow{a}.\) và\(\overrightarrow{b}\) và kí hiệu là \(\overrightarrow{a}.\overrightarrow{b} =
\left| \overrightarrow{a} \right|.\left| \overrightarrow{b}
\right|.cos\left( \overrightarrow{a};\overrightarrow{b}
\right)\)
Về mặt tọa độ: Nếu có \(\overrightarrow{a}
= \left( a_{1};a_{2} \right),\overrightarrow{b} = \left( b_{1};b_{2}
\right)\) thì \(\overrightarrow{a}.\overrightarrow{b} =
a_{1}.a_{2} + b_{1}.b_{2}\)
Hai vectơ vuông góc:
Nếu có \(\overrightarrow{a} = \left(
a_{1};a_{2} \right),\overrightarrow{b} = \left( b_{1};b_{2}
\right)\) thì \(\overrightarrow{a}\bot\overrightarrow{b}
\Leftrightarrow a_{1}b_{2} + a_{2}b_{2} = 0\) (hoành nhân hoành cộng tung nhân tung = 0)
Cos góc giữa hai vectơ:
Nếu có \(\overrightarrow{a} = \left(
a_{1};a_{2} \right),\overrightarrow{b} = \left( b_{1};b_{2}
\right)\) thì \(\cos\left(
\overrightarrow{a},\overrightarrow{b} \right) =
\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a}
\right|.\left| \overrightarrow{b} \right|} = \frac{a_{1}b_{1} +
a_{2}b_{2}}{\sqrt{a_{1}^{2} + a_{2}^{2}}.\sqrt{b_{1}^{2} +
b_{2}^{2}}}\)
Cos góc giữa hai đường thẳng:
Nếu có \(d_{1}:a_{1}x + b_{1}y + c_{1} =
0,\ d_{2}:a_{2}x + b_{2}y + c_{2} = 0\)
\(\cos\left( d_{1};d_{2} \right) = \left|
\cos\left( \overrightarrow{n_{d_{1}}},\overrightarrow{n_{d_{2}}} \right)
\right| = \frac{\left|
\overrightarrow{n_{d_{1}}}.\overrightarrow{n_{d_{2}}} \right|}{\left|
\overrightarrow{n_{d_{1}}} \right|.\left| \overrightarrow{n_{d_{2}}}
\right|} = \frac{\left| a_{1}a_{2} + b_{1}b_{2} \right|}{\sqrt{a_{1}^{2}
+ b_{1}^{2}}.\sqrt{a_{2}^{2} + b_{2}^{2}}}\)
Với \(\overrightarrow{n_{d_{1}}} = \left( a_{1};b_{1}
\right),\overrightarrow{n_{d_{2}}} = \left( a_{2};b_{2}
\right)\)
Điểm thuộc đường thẳng:
Nếu có đường thẳng \(d:ax + by + c =
0\) thì \(A\left( x_{A};y_{A} \right)
\in d \Leftrightarrow ax_{A} + by_{A} + c = 0\).
Khoảng cách từ một điểm đến đường thẳng:
Nếu có đường thẳng \(d:ax + by + c =
0\) và \(A\left( x_{A};y_{A}
\right)\) thì khoảng cách từ điểm A đến đường thẳng d được tính theo công thức \(d\lbrack A,d\rbrack =
\frac{\left| ax_{A} + by_{A} + c \right|}{\sqrt{a^{2} +
b^{2}}}\)
Vị trí tương đối của một điểm so với đường thẳng:
Cho đường thẳng \(d:ax + by + c =
0\) với \(a^{2} + b^{2} \neq 0\) và hai điểm \(A\left( x_{A};y_{A}
\right);B\left( x_{B};y_{B} \right)\)
+Nếu \(\left( ax_{A} + by_{A} + c
\right)\left( ax_{B} + by_{B} + c \right) > 0\) thì A, B nằm cùng một bên (cùng một nửa mặt phẳng bờ là đường thẳng d).
+ Nếu \(\left( ax_{A} + by_{A} + c
\right)\left( ax_{B} + by_{B} + c \right) < 0\) thì A, b nằm khác bên (mỗi điểm nằm mỗi nửa mặt phẳng bờ là đường thẳng d).
Vị trí tương đối của hai đường thẳng:
Cho hai đường thẳng \(d_{1}:a_{1}x + b_{1}y
+ c_{1} = 0\) và \(d_{2}:a_{2}x +
b_{2}y + c_{2} = 0\) (giả sử \(a_{2},b_{2} \neq 0\))
+ Nếu \(\frac{a_{1}}{a_{2}} \neq
\frac{b_{1}}{b_{2}}\) thì hai đường thẳng cắt nhau.
+ Nếu \(\frac{a_{1}}{a_{2}} =
\frac{b_{1}}{b_{1}} \neq \frac{c_{1}}{c_{2}}\) thì hai đường thẳng song song nhau.
+ Nếu \(\frac{a_{1}}{a_{2}} =
\frac{b_{1}}{b_{1}} = \frac{c_{1}}{c_{2}}\) thì hai đường thẳng trùng nhau.
PHẦN II: BÀI TOÁN VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Định nghĩa.
Trong mặt phẳng Oxy, mọi đường thẳng đều có phương trình tổng quát dạng \(ax + by + c = 0\) với \(a^{2} + b^{2} \neq 0\)
Chú ý: Nếu đường thẳng d đi qua điểm \(A\left( x_{A};y_{A} \right)\) và có vectơ pháp tuyến \(\overrightarrow{n_{d}} =
(a;b)\) thì đường thẳng d có phương trình \(d:a\left( x - x_{A} \right) + b\left( y - y_{A}
\right) = 0\)
Chú ý:
- Vectơ pháp tuyến của đường thẳng là vectơ có phương vuông góc với đường thẳng đó.
- Vectơ chỉ phương của đường thẳng là vectơ có phương song song với đường thẳng đó.
- Nếu vectơ chỉ phương là \(\overrightarrow{n_{d}} = (a;b) \Rightarrow
\overrightarrow{u_{d}} = ( - b;a)\)
Dưới đây là hai bài toán viết phương trình đường thẳng biến thể, ở đó chúng ta sẽ sử dụng công thức khoảng cách, hoặc công thức góc để giải quyết.
Bài toán viết phương trình đường thẳng sử dụng khoảng cách:
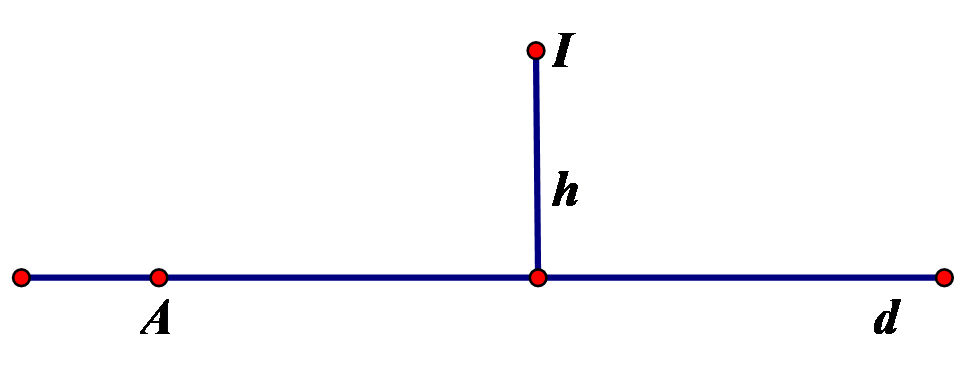
Nếu đường thẳng d đi qua điểm \(A\left(
x_{A};y_{A} \right)\) và khoảng cách từ điểm I (biết tọa độ) đến d bằng h thì ta luôn viết được phương trình đường thẳng d.
Ví dụ: Viết phương trình đường thẳng DM đi qua \(E( - 2; - 1)\) và khoảng cách từ \(I\left( \frac{13}{4};\frac{7}{2} \right)\) đến DM bằng \(\sqrt{\frac{45}{4}}\).
Gọi \(\overrightarrow{n} = (a;b)\) với \(a^{2} + b^{2} \neq 0\) là vectơ pháp tuyến của đường thẳng DM.
Phương trình đường thẳng DM là \(a(x + 2) +
b(y + 1) = 0,\left( a^{2} + b^{2} > 0 \right)\)
\(d(I;DM) = \dfrac{\sqrt{45}}{4}\)\(\Leftrightarrow \dfrac{\left| \dfrac{21}{4}a + \dfrac{9}{2}b
\right|}{\sqrt{a^{2} + b^{2}}} = \dfrac{\sqrt{45}}{4}\)\(\Leftrightarrow |7a
+ 6b| = \sqrt{5\left( a^{2} + b^{2} \right)}\)
\(\Leftrightarrow 44a^{2} + 84ab + 31b^{2}
= 0 \Leftrightarrow \left\lbrack \begin{matrix}
22a = - 31b \\
2a = - b \\
\end{matrix} \right.\)
TH1: Với \(22a = - 31b\) ta chọn \(a = 31;b = - 22\)
Suy ra, phương trình DM là \(31x - 22y + 40
= 0\)
TH2: Với \(2a = - b\) ta chọn \(a = 1;b = - 2\)
Suy ra, phương trình đường thẳng DM là \(x
- 2y = 0\)
Mời các bạn tải đầy đủ tài liệu để tham khảo.
