VnDoc.com

Sự đơn điệu của Hàm số Toán 12 dạng Đúng sai – Có đáp án

Ôn thi THPT Quốc gia môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập đúng sai sự đơn điệu của hàm số - Có đáp án chi tiết

Phần I. Đề bài trắc nghiệm đúng sau Sự đơn điệu của hàm số
Phần II. Đáp án bài tập trắc nghiệm đúng sai Sự đơn điệu của hàm số

Sự đơn điệu của hàm số là chuyên đề trọng tâm trong chương trình Giải tích 12, đồng thời là nội dung thường xuyên xuất hiện trong đề thi THPT Quốc gia môn Toán. Việc nắm vững các kiến thức về tính đồng biến, nghịch biến của hàm số, cũng như kỹ năng xác định khoảng biến thiên giúp học sinh tự tin xử lý các bài toán trắc nghiệm nhanh chóng và chính xác.

Bài viết “Sự đơn điệu của Hàm số Toán 12 dạng Đúng sai – Có đáp án” tổng hợp các câu hỏi trắc nghiệm đúng sai bám sát SGK, kèm đáp án chi tiết và giải thích ngắn gọn, giúp học sinh củng cố kiến thức, rèn luyện phản xạ tư duy và chuẩn bị tốt nhất cho kỳ thi THPT Quốc gia.

Phần I. Đề bài trắc nghiệm đúng sau Sự đơn điệu của hàm số

Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

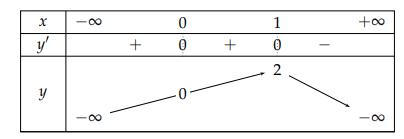
Xét tính đúng sai của các khẳng định dưới đây:

	Đúng	Sai
a) Hàm số đồng biến trên (−∞; 2).
b) Hàm số nghịch biến trên (1; +∞).
c) Hàm số có hai điểm cực trị.
d) Hàm số đạt cực đại tại x = 1.

Câu 2: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ như sau:

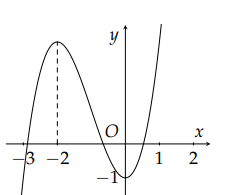
Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Hàm số đã cho nghịch biến trên khoảng (−2, 0).
b) Hàm số đã cho đồng biến trên khoảng (−1; +∞).
c) Hàm số đã cho đồng biến trên khoảng (2; +∞).
d) Hàm số đạt cực tiểu tại x = −1.

Câu 3: Cho hàm số $y = f(x)$ xác định trên tập số thực và có đạo hàm $f'(x) = 3x^{3} - 3x^{2};\left( x\mathbb{\in R} \right)$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Hàm số đồng biến trên khoảng (1; +∞).
b) Hàm số nghịch biến trên khoảng (−1; 1).
c) Đồ thị hàm số có hai điểm cực trị.
d) Đồ thị hàm số có một điểm cực tiểu.

Câu 4: Cho hàm số $y = f(x) = x^{4} - 2x^{2} - 3$ $y = f(x) = x^{4} - 2x^{2} - 3$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Hàm số đã cho đạt cực đại tại x = 0.
b) Hàm số đã cho đạt cực tiểu tại x = −3.
c) Hàm số đã cho có giá trị cực đại và cực tiểu lần lượt là −4, −3.
d) Đồ thị hàm số g(x) = f(x) + 3 có điểm cực đại là (0; 0).

Câu 5: Hàm số $y = f(x)$ liên tục trên đoạn $\lbrack - 1;3\rbrack$ $\lbrack - 1;3\rbrack$ và có bảng biến thiên như sau.

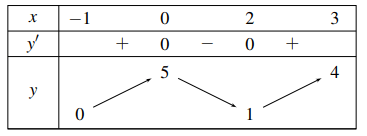
Gọi $M$ và $m$ lần lượt là GTLN và GTNN của hàm số trên $\lbrack - 1;3\rbrack$ $\lbrack - 1;3\rbrack$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) $m = f(2)$.
b) $M = f(4)$.
c) $m = f( - 1)$.
d) $M = f(0)$.

Câu 6: Cho hàm số $y = f(x)$ xác định trên tập $D$ và một số thực $M$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Nếu $f(x) \leq M,\forall x \in D$ $f(x) \leq M,\forall x \in D$ thì $\underset{D}{\max f(x)} = M$ $\underset{D}{\max f(x)} = M$.
b) Nếu $f(x) \geq M,\forall x \in D$ $f(x) \geq M,\forall x \in D$ thì $\underset{D}{\min f(x)} = M$ $\underset{D}{\min f(x)} = M$.
c) Nếu $f(x) = M,\forall x \in D$ $f(x) = M,\forall x \in D$ thì $\underset{D}{\max f(x)} = M$ $\underset{D}{\max f(x)} = M$.
d) Nếu $f(x) = M,\forall x \in D$ $f(x) = M,\forall x \in D$ thì $\underset{D}{\min f(x)} = M$ $\underset{D}{\min f(x)} = M$.

Câu 7: Cho hàm số $y = f(x)$ xác định, liên tục trên R và có bảng biến thiên như hình vẽ dưới đây:

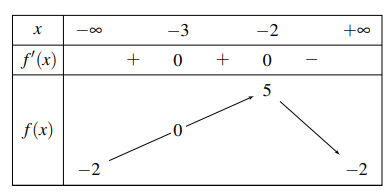
Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Hàm số đồng biến trên khoảng (−2; 5).
b) Hàm số đạt cực đại tại điểm x = −2.
c) Hàm số có giá trị nhỏ nhất bằng −2.
d) Hàm số có giá trị lớn nhất bằng 5.

Câu 8: Cho hàm số $y = f(x) = x^{2} - 4ln(1 - x)$ $y = f(x) = x^{2} - 4ln(1 - x)$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Tập xác định của hàm số là $D = (1; + \infty)$ $D = (1; + \infty)$.
b) Đạo hàm của hàm số là $y' = \frac{- 2x^{2} + 2x + 4}{1 - x}$.
c) Giá trị lớn nhất của hàm số trên $\lbrack - 2;0\rbrack$ $\lbrack - 2;0\rbrack$ là 2.
d) Giá trị nhỏ nhất của hàm số trên $\lbrack - 2;0\rbrack$ $\lbrack - 2;0\rbrack$ là $1 - 4\ln2$ $1 - 4\ln2$.

Câu 9: Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích $1800m^{3}$ $1800m^{3}$ và chiều sâu $2m$ (như hình vẽ).

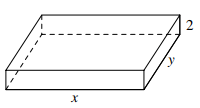
Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Thể tích bể chứa được tính theo công thức $V = 2x^{2}y$ $V = 2x^{2}y$.
b) Mối liên hệ giữa x và y là $y = \frac{900}{x}$ $y = \frac{900}{x}$.
c) Tổng diện tích mặt bên của bể tính theo x, y là $S = 4(x + y)$.
d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là $40m$.

Câu 10: Cho hàm số $y = f(x)$ có:

$\lim_{x \rightarrow 3^{-}}f(x) = 1;\lim_{x \rightarrow 3^{+}}f(x) = + \infty;\lim_{x \rightarrow - \infty}f(x) = 1;\lim_{x \rightarrow + \infty}f(x) = + \infty$ $\lim_{x \rightarrow 3^{-}}f(x) = 1;\lim_{x \rightarrow 3^{+}}f(x) = + \infty;\lim_{x \rightarrow - \infty}f(x) = 1;\lim_{x \rightarrow + \infty}f(x) = + \infty$

Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Đồ thị của hàm số $y = f(x)$ có tiệm cận ngang là đường thẳng $y = 1$.
b) Đồ thị của hàm số $y = f(x)$ có tiệm cận đứng là đường thẳng $x = 3$.
c) Đồ thị của hàm số $y = f(x)$ không có tiệm cận ngang.
d) Đồ thị của hàm số $y = f(x)$ không có tiệm cận đứng.

Câu 11: Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\left\{ \pm 2 \right\}$ $\mathbb{R}\left\{ \pm 2 \right\}$ và có bảng biến thiên như sau:

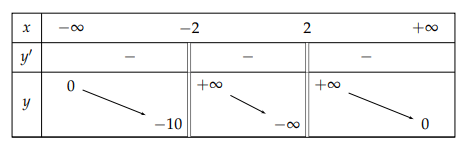
Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Hàm số không có điểm cực trị.
b) $\lim_{x \rightarrow ( - 2)^{-}}f(x) = + \infty$ $\lim_{x \rightarrow ( - 2)^{-}}f(x) = + \infty$.
c) Đồ thị hàm số có đúng 1 tiệm cận ngang.
d) Đồ thị hàm số có đúng 1 tiệm cận đứng.

Câu 12: Cho hàm số $y = f(x) = \frac{\sqrt{x^{2} - x + 2}}{x - 1}$ $y = f(x) = \frac{\sqrt{x^{2} - x + 2}}{x - 1}$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Tập xác định của hàm số là $\mathbb{R}\backslash\left\{ 1 \right\}$ $\mathbb{R}\backslash\left\{ 1 \right\}$.
b) Đồ thị hàm số có các đường tiệm cận ngang là $y = 1,\ y = - 1$ $y = 1,\ y = - 1$.
c) Đồ thị hàm số đã cho có tất cả 2 đường tiệm cận.
d) Các đường tiệm cận của đồ thị cùng với trục Oy tạo thành 1 đa giác có diện tích bằng 1.

Phần II. Đáp án bài tập trắc nghiệm đúng sai Sự đơn điệu của hàm số

Câu 1:

Quan sát bảng biến thiên, ta có các kết quả sau:

a) Hàm số đồng biến trên (−∞; 1) nên khẳng định hàm số đồng biến trên (−∞; 2) là sai.

b) Hàm số nghịch biến trên (1; +∞).

c) Hàm số có đúng 1 điểm cực trị là x = 1.

d) Hàm số có đạt cực đại tại x = 1.

Câu 2:

Ta có thể từ đồ thị thiết lập lại bảng biến thiên như sau:

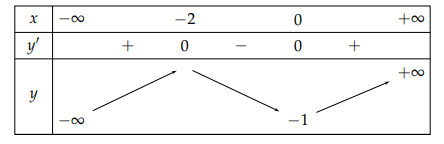
a) Hàm số nghịch biến trên khoảng (−2, 0).

b) Hàm số đồng biến trên khoảng (0; +∞) nên khẳng định đồng biến trên khoảng (−1; +∞) là sai.

c) Hàm số đồng biến trên khoảng (0; +∞) nên nên hàm số đồng biến trên khoảng (2; +∞).

d) Hàm số đạt cực tiểu tại x = 0 (chú ý y = −1 gọi là giá trị cực tiểu).

Câu 3:

Ta có: $f'(x) = 0 \Leftrightarrow 3x^{3} - 3x^{2} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \end{matrix} \right.$

Bảng biến thiên:

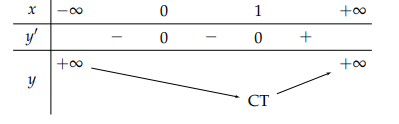
a) Hàm số đồng biến trên khoảng (1; +∞).

b) Hàm số nghịch biến trên khoảng (−∞; 1) nên nghịch biến trên (−1; 1).

c) Hàm số có đúng một điểm cực trị.

d) Hàm số có đúng một điểm cực tiểu x = 1.

Câu 4:

Ta có: $f'(x) = 4x^{3} - 4x \Rightarrow f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 0 \\ x = 1 \end{matrix} \right.$

Bảng biến thiên:

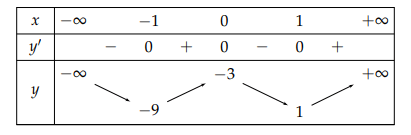
a) Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại x = 0

b) Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại x = −3

c) Dựa vào bảng biến thiên ta thấy hàm số giá trị cực đại và cực tiểu lần lượt là −4, −3

d) Dựa vào bảng biến thiên ta thấy hàm số g(x) = f(x) + 3 có được bằng cách tịnh tiến đồ thị y = f(x) lên trên 3 đơn vị. Suy ra đồ thị hàm số g(x) = f(x) + 3 có điểm cực đại là (0; 0).

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

----------------------------------------------------

Thông qua bộ trắc nghiệm đúng sai Sự đơn điệu của Hàm số Toán 12 có đáp án, học sinh sẽ dễ dàng nhận diện các dạng bài thường gặp, hiểu sâu bản chất của sự đồng biến – nghịch biến và áp dụng hiệu quả vào các bài thi trắc nghiệm. Hãy tiếp tục ôn luyện với các chuyên đề hàm số, cực trị, giá trị lớn nhất – nhỏ nhất để củng cố nền tảng kiến thức vững chắc và đạt kết quả cao trong kỳ thi THPT Quốc gia môn Toán.

Tải về

Chọn file muốn tải về: