Tìm tham số m để phương trình có n nghiệm (dựa vào bảng biến thiên)
Bài toán tương giao đồ thị hàm số chứa tham số m
Trong chương trình Toán 12, dạng bài tìm tham số m để phương trình có n nghiệm là một nội dung trọng tâm, thường xuyên xuất hiện trong các đề thi THPT Quốc gia. Một trong những phương pháp giải nhanh và chính xác là phân tích dựa vào bảng biến thiên của hàm số. Phương pháp này giúp học sinh xác định số nghiệm phương trình thông qua tính đơn điệu, cực trị và dấu của hàm số, thay vì chỉ dựa vào đồ thị. Bài viết này sẽ hướng dẫn bạn cách sử dụng bảng biến thiên để tìm tham số m hiệu quả, kèm ví dụ minh họa chi tiết và đáp án chuẩn, giúp bạn nắm chắc kỹ năng làm bài.
A. Ví dụ minh họa tìm m để phương trình có nghiệm theo BBT
Ví dụ 1. Cho hàm số ![]() \(y = f(x)\) có bảng biến thiên như sau:
\(y = f(x)\) có bảng biến thiên như sau:
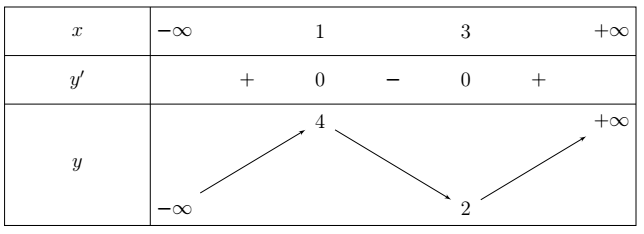
Phương trình ![]() \(f(x) - 2m = 0\) có 3 nghiệm khi
\(f(x) - 2m = 0\) có 3 nghiệm khi
A. ![]() \(- 1 \leq m \leq 2\). B.
\(- 1 \leq m \leq 2\). B. ![]() \(1 < m < 2\). C.
\(1 < m < 2\). C. ![]() \(- 1 < m \leq 2\). D.
\(- 1 < m \leq 2\). D. ![]() \(- 2 < m < 4\).
\(- 2 < m < 4\).
Hướng dẫn giải
Chọn B
Ta có: ![]() \(f(x) - 2m = 0 \Leftrightarrow f(x)
= 2m\)
\(f(x) - 2m = 0 \Leftrightarrow f(x)
= 2m\) ![]() \((1)\).
\((1)\).
Để ![]() \((1)\) có 3 nghiệm thì:
\((1)\) có 3 nghiệm thì: ![]() \(2 < 2m < 4 \Leftrightarrow 1 < m <
2\).
\(2 < 2m < 4 \Leftrightarrow 1 < m <
2\).
Ví dụ 2. Cho hàm số ![]() \(f(x)\) liên tục trên
\(f(x)\) liên tục trên ![]() \(\mathbb{R}\) và có bảng biến thiên như hình vẽ dưới đây.
\(\mathbb{R}\) và có bảng biến thiên như hình vẽ dưới đây.
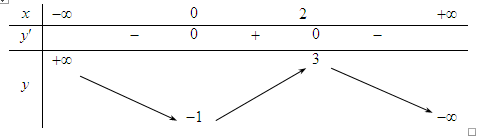
Tìm tất cả các giá trị của tham số thực ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(f(x) = 2m + 1\) có
\(f(x) = 2m + 1\) có ![]() \(3\) nghiệm phân biệt.
\(3\) nghiệm phân biệt.
A. ![]() \(- 1 < m < 1\). B.
\(- 1 < m < 1\). B. ![]() \(- 1 < m < 3\). C.
\(- 1 < m < 3\). C. ![]() \(0 < m < 2\). D.
\(0 < m < 2\). D. ![]() \(- \frac{1}{2} < m <
\frac{1}{2}\).
\(- \frac{1}{2} < m <
\frac{1}{2}\).
Hướng dẫn giải
Chọn A
Dựa vào bảng biến thiên ta có: phương trình ![]() \(f(x) = 2m + 1\) có
\(f(x) = 2m + 1\) có ![]() \(3\) nghiệm phân biệt khi
\(3\) nghiệm phân biệt khi ![]() \(- 1 < 2m + 1 < 3 \Leftrightarrow - 1 < m
< 1\).
\(- 1 < 2m + 1 < 3 \Leftrightarrow - 1 < m
< 1\).
Ví dụ 3. Cho hàm số ![]() \(y = f(x)\) có bảng biến thiên như sau:
\(y = f(x)\) có bảng biến thiên như sau:
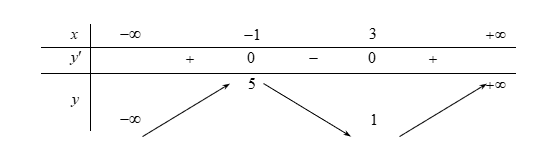
Số Số nghiệm của phương trình ![]() \(\left| f(x)
\right| - 2 = 0\) là:
\(\left| f(x)
\right| - 2 = 0\) là:
A. ![]() \(2\). B.
\(2\). B. ![]() \(1\). C.
\(1\). C. ![]() \(3\). D.
\(3\). D. ![]() \(4\).
\(4\).
Hướng dẫn giải
Từ bảng biến thiên của hàm số ![]() \(y =
f(x)\) ta có bảng biến thiên của hàm số
\(y =
f(x)\) ta có bảng biến thiên của hàm số ![]() \(y = \left| f(x) \right|\) như sau:
\(y = \left| f(x) \right|\) như sau:
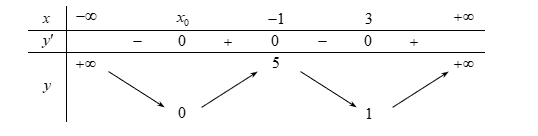
Gọi ![]() \(x_{0}\) là giá trị thỏa mãn
\(x_{0}\) là giá trị thỏa mãn ![]() \(f\left( x_{0} \right) = 0\).
\(f\left( x_{0} \right) = 0\).
Dựa vào bảng biến thiên của hàm số ![]() \(y =
\left| f(x) \right|\) ta đưa ra kết luận về số nghiệm của phương trình
\(y =
\left| f(x) \right|\) ta đưa ra kết luận về số nghiệm của phương trình ![]() \(\left| f(x) \right| - 2 = 0\) là
\(\left| f(x) \right| - 2 = 0\) là ![]() \(4\) nghiệm.
\(4\) nghiệm.
Ví dụ 4. Cho hàm số ![]() \(y = f(x)\) xác định, liên tục trên
\(y = f(x)\) xác định, liên tục trên ![]() \(\mathbb{R}\) và có bảng biến thiên sau:
\(\mathbb{R}\) và có bảng biến thiên sau:
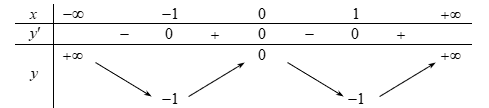
Tìm tất cả các giá trị thực của tham số ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(f(x) - 1 = m\) có đúng hai nghiệm.
\(f(x) - 1 = m\) có đúng hai nghiệm.
A. ![]() \(m = - 2,\ m \geq - 1\). B.
\(m = - 2,\ m \geq - 1\). B. ![]() \(m > 0,\ m = - 1\).
\(m > 0,\ m = - 1\).
C. ![]() \(m = - 2,m > - 1\). D.
\(m = - 2,m > - 1\). D. ![]() \(- 2 < m < - 1\).
\(- 2 < m < - 1\).
Hướng dẫn giải
Chọn C
Ta có ![]() \(f(x) - 1 = m \Leftrightarrow f(x) =
m + 1\).
\(f(x) - 1 = m \Leftrightarrow f(x) =
m + 1\).
Dựa vào bảng biến thiên, để phương trình có đúng hai nghiệm thì ![]() \(\left\lbrack \begin{matrix}
m + 1 = - 1 \\
m + 1 > 0
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
m = - 2 \\
m > - 1
\end{matrix} \right.\)
\(\left\lbrack \begin{matrix}
m + 1 = - 1 \\
m + 1 > 0
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
m = - 2 \\
m > - 1
\end{matrix} \right.\)
B. Bài tập tự rèn luyện tìm m có đáp án chi tiết
Bài tập 1. Cho hàm số ![]() \(y =
f(x)\) xác định trên
\(y =
f(x)\) xác định trên ![]() \(R\backslash\left\{
- 1;1 \right\}\), liên tục trên từng khoảng xác định và có bảng biên thiên sau:
\(R\backslash\left\{
- 1;1 \right\}\), liên tục trên từng khoảng xác định và có bảng biên thiên sau:
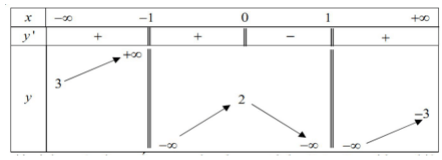
Tìm tất cả các giá trị của tham số ![]() \(m\)sao cho phương trình
\(m\)sao cho phương trình ![]() \(f(x) = 3m\) có ba nghiệm phân biệt.
\(f(x) = 3m\) có ba nghiệm phân biệt.
A. ![]() \(- 1 < m < \frac{-
2}{3}\). B.
\(- 1 < m < \frac{-
2}{3}\). B. ![]() \(m < - 1\). C.
\(m < - 1\). C. ![]() \(m \leq - 1\). D.
\(m \leq - 1\). D. ![]() \(A = \sqrt{7}\).
\(A = \sqrt{7}\).
Bài tập 2. Cho hàm số ![]() \(y = f(x)\) xác định trên
\(y = f(x)\) xác định trên ![]() \(\mathbb{R}\backslash\left\{ -
1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau:
\(\mathbb{R}\backslash\left\{ -
1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau:
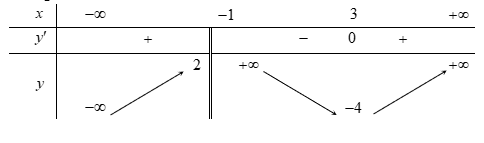
Tìm tập hợp tất cả các giá trị của tham số thực ![]() \(m\) sao cho phương trình
\(m\) sao cho phương trình ![]() \(f(x) = m\) có đúng ba nghiệm thực phân biệt
\(f(x) = m\) có đúng ba nghiệm thực phân biệt
A. ![]() \(( - 4;2)\). B.
\(( - 4;2)\). B. ![]() \(\lbrack - 4;2)\). C.
\(\lbrack - 4;2)\). C. ![]() \(( - 4;2\rbrack\). D.
\(( - 4;2\rbrack\). D. ![]() \(( - \infty;2\rbrack\).
\(( - \infty;2\rbrack\).
Bài tập 3. Cho hàm số ![]() \(y = f(x)\) xác định, liên tục trên
\(y = f(x)\) xác định, liên tục trên ![]() \(\mathbb{R}\backslash\left\{ 1 \right\}\) và có bảng biến thiên như sau:
\(\mathbb{R}\backslash\left\{ 1 \right\}\) và có bảng biến thiên như sau:
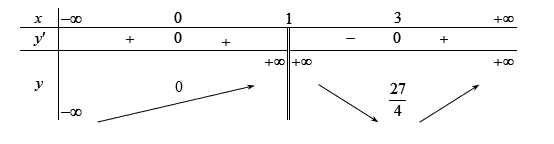
Tìm điều kiện của ![]() \(m\) để phương trình
\(m\) để phương trình ![]() \(f(x) = m\) có 3 nghiệm phân biệt.
\(f(x) = m\) có 3 nghiệm phân biệt.
A. ![]() \(m < 0\). B.
\(m < 0\). B. ![]() \(m > 0\). C.
\(m > 0\). C. ![]() \(0 < m < \frac{27}{4}\). D.
\(0 < m < \frac{27}{4}\). D. ![]() \(m > \frac{27}{4}\).
\(m > \frac{27}{4}\).
Bài tập 4. Cho hàm số ![]() \(y = f(x)\) xác định trên
\(y = f(x)\) xác định trên ![]() \(\mathbb{R}\backslash\left\{ 0
\right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
\(\mathbb{R}\backslash\left\{ 0
\right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
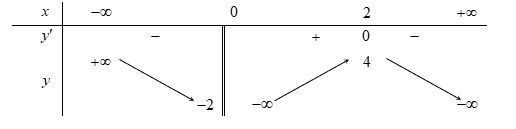
Tìm tập hợp tất cả các giá trị thực của tham số ![]() \(m\) sao cho phương trình
\(m\) sao cho phương trình ![]() \(f(x) = m\) có ba nghiệm thực phân biệt.
\(f(x) = m\) có ba nghiệm thực phân biệt.
A. ![]() \(\lbrack - 2;4\rbrack\). B.
\(\lbrack - 2;4\rbrack\). B. ![]() \(( - 2;4)\). C.
\(( - 2;4)\). C. ![]() \(( - 2;4\rbrack\). D.
\(( - 2;4\rbrack\). D. ![]() \(( - \infty;4\rbrack\).
\(( - \infty;4\rbrack\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
--------------------------------------------
Bài toán tìm tham số m để phương trình có n nghiệm dựa vào bảng biến thiên giúp học sinh hiểu sâu bản chất của hàm số, đồng thời luyện khả năng tư duy logic và phân tích đồ thị gián tiếp. Với các bước giải rõ ràng, ví dụ cụ thể và đáp án chi tiết, hy vọng bài viết này sẽ giúp bạn làm chủ dạng bài chứa tham số m và đạt điểm tối đa trong phần hàm số của đề thi.










