VnDoc.com

Chuyên đề Trắc nghiệm đúng sai Hệ tọa độ trong không gian Oxyz

Ôn thi THPT Quốc gia môn Toán Có đáp án chi tiết

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Trắc nghiệm

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bộ câu hỏi trắc nghiệm đúng sai phương trình mặt cầu trong Oxyz

Phần I. Đề bài trắc nghiệm đúng sai
Phần II. Đáp án chi tiết bài tập trắc nghiệm đúng sai

Trong chương trình Toán 12, chủ đề phương trình mặt cầu trong không gian Oxyz là một phần quan trọng của hình học không gian và thường xuyên xuất hiện trong đề thi THPT Quốc gia môn Toán. Để giúp học sinh nắm chắc kiến thức, bài viết này tổng hợp bộ câu hỏi trắc nghiệm đúng sai phương trình mặt cầu trong Oxyz kèm đáp án chi tiết, giúp các em kiểm tra mức độ hiểu bài, rèn luyện khả năng phân tích và vận dụng công thức vào giải quyết bài tập thực tế.

Nội dung được biên soạn bám sát chương trình SGK Toán 12, phù hợp cho học sinh ôn thi, củng cố kiến thức và chuẩn bị tốt nhất cho các kỳ kiểm tra sắp tới.

Phần I. Đề bài trắc nghiệm đúng sai

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết rằng: cạnh AB = a, AD = 2a, cạnh bên SA = 2a và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD. Xét tính đúng sai của các khẳng định sau.

	Đúng	Sai
a) Hai vectơ $\overrightarrow{AB};\overrightarrow{CD}$ $\overrightarrow{AB};\overrightarrow{CD}$ là hai vectơ cùng phương, cùng hướng.
b) Góc giữa hai vectơ $\overrightarrow{SC};\overrightarrow{AC}$ $\overrightarrow{SC};\overrightarrow{AC}$ bằng $60^{0}$ $60^{0}$.
c) Tích vô hướng của $\overrightarrow{AM};\overrightarrow{AB}$ $\overrightarrow{AM};\overrightarrow{AB}$ bằng $\frac{a^{2}}{2}$ $\frac{a^{2}}{2}$.
d) Độ dài vectơ $\overrightarrow{AM} - \overrightarrow{AN}$ $\overrightarrow{AM} - \overrightarrow{AN}$ là $\frac{a\sqrt{3}}{2}$ $\frac{a\sqrt{3}}{2}$.

Câu 2: Trong không gian $Oxyz$, cho tam giác $ABC$ với tọa độ các điểm $A(1;0; - 2),B( - 2;3;4),C(4; - 6;1)$. Xác định tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Tọa độ trọng tâm G của tam giác là $(1; - 1;1)$.
b) $\overrightarrow{AB} = (3; - 3;6),\overrightarrow{AC} = ( - 3;6; - 3)$ $\overrightarrow{AB} = (3; - 3;6),\overrightarrow{AC} = ( - 3;6; - 3)$.
c) Tam giác $ABC$ là tam giác cân.
d) Nếu $ABDC$ là hình bình hành thì tọa độ điểm D là $(7; - 9; - 5)$.

Câu 3: Trong không gian $Oxyz$, cho vectơ $\overrightarrow{OA} = (2; - 1;5),B(5; - 5;7)$ $\overrightarrow{OA} = (2; - 1;5),B(5; - 5;7)$ và điểm B(5; 5;-7).

Xét sự đúng sai của các khẳng định dưới đây:

	Đúng	Sai
a) Tọa độ của điểm $A$ là $(2; - 1;5)$.
b) Gọi $C(a;b;c)$ thỏa mãn ∆ABC nhận G(1;1;1) làm trọng tâm. Khi đó $a + b + c = - 4$.
c) Nếu $A;B;M(x;y;1)$ thẳng hàng thì tổng $x + y = 3$.
d) Cho $N \in (Oxy)$ $N \in (Oxy)$ để ∆ABN vuông cân tại A. Tổng hoành độ và tung độ của điểm N bằng 3.

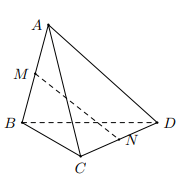
Câu 4: Cho tứ diện ABCD. Gọi M, N theo thứ tự là trung điểm AB và CD. Xác định tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) $\overrightarrow{MC} + \overrightarrow{MD} + \overrightarrow{NA} + \overrightarrow{NB} = 4\overrightarrow{MN}$ $\overrightarrow{MC} + \overrightarrow{MD} + \overrightarrow{NA} + \overrightarrow{NB} = 4\overrightarrow{MN}$.
b) $\overrightarrow{AC} + \overrightarrow{BD} = 2\overrightarrow{MN}$ $\overrightarrow{AC} + \overrightarrow{BD} = 2\overrightarrow{MN}$.
c) $\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{MN}$ $\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{MN}$.
d) $\overrightarrow{AC} + \overrightarrow{AD} = 2\overrightarrow{AN}$ $\overrightarrow{AC} + \overrightarrow{AD} = 2\overrightarrow{AN}$.

Câu 5: Trong không gian Oxyz, cho vectơ $\overrightarrow{OA} = - 2\overrightarrow{i} + 4\overrightarrow{j} + 2\overrightarrow{k}$ $\overrightarrow{OA} = - 2\overrightarrow{i} + 4\overrightarrow{j} + 2\overrightarrow{k}$. Các khẳng định sau là đúng hay sai?

	Đúng	Sai
a) Tọa độ điểm A là (−2; 4; 2).
b) Hình chiếu vuông góc của A lên trục Ox là A’(0; 4; 0).
c) Trung điểm của OA là M(−1; 2; 1).
d) Hình chiếu vuông góc của A lên mặt phẳng (Oyz) là H(−2; 0; 2).

Câu 6: Cho tứ diện $ABCD$. Gọi $M;N;P;Q;R;S;G$lần lượt là trung điểm các đoạn thẳng $AB;CD;AC;BD;AD;BC;MN$.

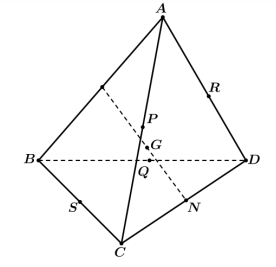
Xét tính đúng sai của các khẳng định sau.

	Đúng	Sai
a) $\overrightarrow{MR} = \overrightarrow{SN}$ $\overrightarrow{MR} = \overrightarrow{SN}$.
b) $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}$ $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}$.
c) $2\overrightarrow{PQ} = \overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AD}$ $2\overrightarrow{PQ} = \overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AD}$.
d) $\left\| \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} \right\|$ $\left\| \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} \right\|$ nhỏ nhất khi và chỉ khi điểm I trùng với điểm G.

Câu 7: Cho tứ diện đều $ABCD$ cạnh $a$. $E$ là điểm trên đoạn $CD$ sao cho $ED = 2CE$. Xét tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) Có 6 vectơ (khác vectơ $\overrightarrow{0}$ $\overrightarrow{0}$ ) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện.
b) Góc giữa hai vectơ $\overrightarrow{AB}$ $\overrightarrow{AB}$ và $\overrightarrow{BC}$ $\overrightarrow{BC}$ bằng $60^{\circ}$ $60^{\circ}$.
c) Nếu $\overrightarrow{BE} = m\overrightarrow{BA} + n\overrightarrow{BC} + p\overrightarrow{BD}$ $\overrightarrow{BE} = m\overrightarrow{BA} + n\overrightarrow{BC} + p\overrightarrow{BD}$ thì $m + n + p = \frac{2}{3}$ $m + n + p = \frac{2}{3}$.
d) Tích vô hướng $\overrightarrow{AD}.\overrightarrow{BE} = \frac{a^{2}}{6}$ $\overrightarrow{AD}.\overrightarrow{BE} = \frac{a^{2}}{6}$.

Câu 8: Cho hình hộp chữ nhật $ABCD.EFGH$ có $AB = AE = 2,AD = 3$ và đặt $\overrightarrow{a} = \overrightarrow{AB},\overrightarrow{b} = \overrightarrow{AD},\overrightarrow{c} = \overrightarrow{AE}$ $\overrightarrow{a} = \overrightarrow{AB},\overrightarrow{b} = \overrightarrow{AD},\overrightarrow{c} = \overrightarrow{AE}$. Lấy điểm $M$ thỏa $\overrightarrow{AM} = \frac{1}{5}\overrightarrow{AD}$ $\overrightarrow{AM} = \frac{1}{5}\overrightarrow{AD}$ và điểm $N$ thỏa $\overrightarrow{EN} = \frac{2}{5}\overrightarrow{EC}$ $\overrightarrow{EN} = \frac{2}{5}\overrightarrow{EC}$. (Quan sát hình vẽ).

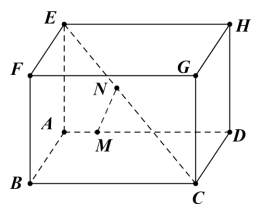
Xác định tính đúng sai của các khẳng định sau:

	Đúng	Sai
a) $\overrightarrow{MA} = - \frac{1}{5}\overrightarrow{b}$ $\overrightarrow{MA} = - \frac{1}{5}\overrightarrow{b}$.
b) $\overrightarrow{EN} = \frac{2}{5}\left( \overrightarrow{a} - \overrightarrow{b} + \overrightarrow{c} \right)$ $\overrightarrow{EN} = \frac{2}{5}\left( \overrightarrow{a} - \overrightarrow{b} + \overrightarrow{c} \right)$.
c) $\left( m\overrightarrow{a} + n\overrightarrow{b} + p\overrightarrow{c} \right)^{2} = m^{2}\overrightarrow{a^{2}} + n^{2}\overrightarrow{b^{2}} + p^{2}\overrightarrow{c^{2}}$ $\left( m\overrightarrow{a} + n\overrightarrow{b} + p\overrightarrow{c} \right)^{2} = m^{2}\overrightarrow{a^{2}} + n^{2}\overrightarrow{b^{2}} + p^{2}\overrightarrow{c^{2}}$, với $m;n;p$ là các số thực.
d) $MN = \frac{\sqrt{61}}{5}$ $MN = \frac{\sqrt{61}}{5}$.

Câu 9: Trong không gian với hệ trục tọa độ $Oxyz$, cho $\overrightarrow{OA} = 3\overrightarrow{i} - \overrightarrow{k}$ $\overrightarrow{OA} = 3\overrightarrow{i} - \overrightarrow{k}$, với $\overrightarrow{i}, \overrightarrow{k}$ $\overrightarrow{i}, \overrightarrow{k}$ là hai véctơ đơn vị trên hai trục tọa độ $Ox,Oz$, hai điểm $B( - 1;2;3),C(1;4;1)$.

	Đúng	Sai
a) $A(3;0; - 1)$.
b) Ba điểm $A,B,C$ thẳng hàng.
c) Điểm $D(a;b;c)$ là điểm đối xứng của với $A$ qua $B$. Khi đó $a + b + c = 6$.
d) Điểm $M(m;n;p)$ trên mặt phẳng $(Oxy)$ sao cho $MA^{2} + MB^{2} + MC^{2}$ $MA^{2} + MB^{2} + MC^{2}$ đạt giá trị nhỏ nhất. Khi đó $2m - n + 2024p = 0$.

Câu 10: Trong không gian với hệ trục tọa độ $Oxyz$, cho ba điểm $A(1;2;3),B(2;1;5),C(2;4;2)$. Xét sự đúng sai của các khẳng định sau:

	Đúng	Sai
a) Tọa độ trung điểm của $AB$ là $\left( \frac{3}{2};\frac{3}{2};4 \right)$ $\left( \frac{3}{2};\frac{3}{2};4 \right)$.
b) $\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = (5;7;10)$ $\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = (5;7;10)$.
c) Góc giữa hai đường thẳng $AB$ và $AC$ bằng $30^{\circ}$ $30^{\circ}$.
d) Điểm $I(a;b;c)$ nằm trên mặt phẳng $(Oxz)$ thỏa mãn $T = \|3\overrightarrow{IB} - \overrightarrow{IC}\|$ $T = \|3\overrightarrow{IB} - \overrightarrow{IC}\|$ đạt giá trị nhỏ nhất. Khi đó $a - 2b + 2c = 15$.

Phần II. Đáp án chi tiết bài tập trắc nghiệm đúng sai

Câu 1:

Hình vẽ minh họa:

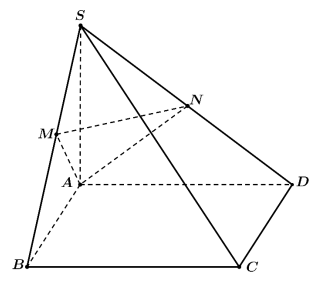
a) Sai

Ta thấy ABCD là hình chữ nhật nên AB//CD

Suy ra hai vectơ $\overrightarrow{AB};\overrightarrow{CD}$ $\overrightarrow{AB};\overrightarrow{CD}$ là hai vectơ cùng phương, ngược hướng.

b) Sai

Ta có ABCD là hình chữ nhật nên $AC = \sqrt{AB^{2} + AD^{2}} = a\sqrt{5}$ $AC = \sqrt{AB^{2} + AD^{2}} = a\sqrt{5}$

Hình chóp S.ABCD có SA vuông góc với mặt đáy nên tam giác SAC là tam giác vuông tại A.

Suy ra $\tan\widehat{SAC} = \frac{SA}{SC} = \frac{2a}{a\sqrt{5}} \Rightarrow \widehat{SAC} \approx 41^{0}48$ $\tan\widehat{SAC} = \frac{SA}{SC} = \frac{2a}{a\sqrt{5}} \Rightarrow \widehat{SAC} \approx 41^{0}48'$

Ta có: $\left( \overrightarrow{SC};\overrightarrow{AC} \right) = \left( \overrightarrow{CS};\overrightarrow{CA} \right) = \widehat{SAC} \approx 41^{0}48$ $\left( \overrightarrow{SC};\overrightarrow{AC} \right) = \left( \overrightarrow{CS};\overrightarrow{CA} \right) = \widehat{SAC} \approx 41^{0}48'$

c) Đúng

Hình chóp S. ABCD có SA vuông góc với mặt đáy nên tam giác SAB là tam giác vuông tại A. Suy ra $SB = \sqrt{SA^{2} + AB^{2}} = a\sqrt{5}$ $SB = \sqrt{SA^{2} + AB^{2}} = a\sqrt{5}$

Trong tam giác SAB vuông tại A có AM là đường trung tuyến nên:

$AM = \frac{1}{2}SB = \frac{a\sqrt{5}}{2}$ $AM = \frac{1}{2}SB = \frac{a\sqrt{5}}{2}$

Lại có M là trung điểm của SB nên $MB = \frac{1}{2}SB = \frac{a\sqrt{5}}{2}$ $MB = \frac{1}{2}SB = \frac{a\sqrt{5}}{2}$

Ta tính được $\cos MAB = \frac{MA^{2} + AB^{2} - MB^{2}}{2MA.AB} = \frac{\sqrt{5}}{5}$ $\cos MAB = \frac{MA^{2} + AB^{2} - MB^{2}}{2MA.AB} = \frac{\sqrt{5}}{5}$

Mà $\left( \overrightarrow{AM};\overrightarrow{AB} \right) = \widehat{MAB}$ $\left( \overrightarrow{AM};\overrightarrow{AB} \right) = \widehat{MAB}$

$\Rightarrow \overrightarrow{AM}.\overrightarrow{AB} = \left| \overrightarrow{AM} \right|.\left| \overrightarrow{AB} \right|.cos\left( \overrightarrow{AM};\overrightarrow{AB} \right) = \frac{a\sqrt{5}}{2}.a.\frac{\sqrt{5}}{5} = \frac{a^{2}}{2}$ $\Rightarrow \overrightarrow{AM}.\overrightarrow{AB} = \left| \overrightarrow{AM} \right|.\left| \overrightarrow{AB} \right|.cos\left( \overrightarrow{AM};\overrightarrow{AB} \right) = \frac{a\sqrt{5}}{2}.a.\frac{\sqrt{5}}{5} = \frac{a^{2}}{2}$

d) Sai

Ta có: M, N lần lượt là trung điểm của các cạnh SB, SD nên MN là đường trung bình của tam giác SBD

Do đó $MN = \frac{1}{2}BD = \sqrt{AB^{2} + AD^{2}} = \frac{a\sqrt{5}}{2}$ $MN = \frac{1}{2}BD = \sqrt{AB^{2} + AD^{2}} = \frac{a\sqrt{5}}{2}$

Suy ra $\left| \overrightarrow{AM} - \overrightarrow{AN} \right| = \left| \overrightarrow{MN} \right| = \frac{a\sqrt{5}}{2}$ $\left| \overrightarrow{AM} - \overrightarrow{AN} \right| = \left| \overrightarrow{MN} \right| = \frac{a\sqrt{5}}{2}$

Câu 2:

a) Đúng.

Trọng tâm tam giác có tọa độ là:

$\left\{ \begin{matrix} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} = 1 \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} = - 1 \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} = 1 \end{matrix} \right.\ \Rightarrow G(1; - 1;1)$ $\left\{ \begin{matrix} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} = 1 \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} = - 1 \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} = 1 \end{matrix} \right.\ \Rightarrow G(1; - 1;1)$

b) Sai. Vì $\overrightarrow{AB} = ( - 3;3;6),\overrightarrow{AC} = (3; - 6;3)$ $\overrightarrow{AB} = ( - 3;3;6),\overrightarrow{AC} = (3; - 6;3)$

c) Đúng. Do $AB = AC = 3\sqrt{6}$ $AB = AC = 3\sqrt{6}$ nên tam giác ABC cân tại A.

d) Sai. Gọi $D(x;y;z)$, vì ABCD là hình bình hành nên

$\overrightarrow{AB} = \overrightarrow{CD} \Leftrightarrow ( - 3;3;6) = (x - 4;y + 6;z - 1)$ $\overrightarrow{AB} = \overrightarrow{CD} \Leftrightarrow ( - 3;3;6) = (x - 4;y + 6;z - 1)$

$\Leftrightarrow (x;y;z) = (1; - 3;7)$ $\Leftrightarrow (x;y;z) = (1; - 3;7)$

Câu 3:

a) Ta có: Tọa độ của điểm $A$ là $(2; - 1;5)$.

b) G là trọng tâm tam giác ABC

$\Leftrightarrow \left\{ \begin{matrix} 1 = \frac{2 + 5 + x_{C}}{3} \\ 1 = \frac{- 1 - 5 + y_{C}}{3} \\ 1 = \frac{5 + 7 + x_{C}}{3} \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{C} = - 4 \\ y_{C} = 9 \\ x_{C} = - 9 \end{matrix} \right.\ \Rightarrow C( - 4;9; - 9)$ $\Leftrightarrow \left\{ \begin{matrix} 1 = \frac{2 + 5 + x_{C}}{3} \\ 1 = \frac{- 1 - 5 + y_{C}}{3} \\ 1 = \frac{5 + 7 + x_{C}}{3} \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{C} = - 4 \\ y_{C} = 9 \\ x_{C} = - 9 \end{matrix} \right.\ \Rightarrow C( - 4;9; - 9)$

$\Rightarrow a + b + c = - 4$ $\Rightarrow a + b + c = - 4$

c) Ta có: $\overrightarrow{AB} = (3; - 4;2);\overrightarrow{AC} = (x - 2;y + 1; - 4)$ $\overrightarrow{AB} = (3; - 4;2);\overrightarrow{AC} = (x - 2;y + 1; - 4)$

Ba điểm A, B, M thằng hàng khi và chỉ khi

$\overrightarrow{AM} = k\overrightarrow{AB} \Leftrightarrow \left\{ \begin{matrix} x - 2 = 3k \\ y + 1 = k.( - 4) \\ - 4 = k.2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = - 4 \\ y = 7 \\ k = - 2 \end{matrix} \right.$ $\overrightarrow{AM} = k\overrightarrow{AB} \Leftrightarrow \left\{ \begin{matrix} x - 2 = 3k \\ y + 1 = k.( - 4) \\ - 4 = k.2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = - 4 \\ y = 7 \\ k = - 2 \end{matrix} \right.$

Suy ra $x + y = 3$

d) Ta có: $N \in (Oxy) \Rightarrow N = (x;y;0)$ $N \in (Oxy) \Rightarrow N = (x;y;0)$

$\Rightarrow \overrightarrow{AN} = (x - 2;y + 1; - 5),\overrightarrow{AB} = (3; - 4;2)$ $\Rightarrow \overrightarrow{AN} = (x - 2;y + 1; - 5),\overrightarrow{AB} = (3; - 4;2)$

Ta có ∆ABN vuông cân tại A $\Leftrightarrow \left\{ \begin{matrix} AN\bot AB(*) \\ AN = AB(**) \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} AN\bot AB(*) \\ AN = AB(**) \end{matrix} \right.$

Từ (*) $\Leftrightarrow \overrightarrow{AN}\bot\overrightarrow{AB} \Leftrightarrow 3(x - 2) - 4(y + 1) - 10 = 0$ $\Leftrightarrow \overrightarrow{AN}\bot\overrightarrow{AB} \Leftrightarrow 3(x - 2) - 4(y + 1) - 10 = 0$

$\Leftrightarrow 3x - 4y = 20 \Leftrightarrow y = \frac{3}{4}x - 5$ $\Leftrightarrow 3x - 4y = 20 \Leftrightarrow y = \frac{3}{4}x - 5$

Từ (**) $AN^{2} = AB^{2} \Leftrightarrow (x - 2)^{2} + (y + 1)^{2} + 25 = 9 + 16 + 4$ $AN^{2} = AB^{2} \Leftrightarrow (x - 2)^{2} + (y + 1)^{2} + 25 = 9 + 16 + 4$

$\Leftrightarrow (x - 2)^{2} + \left( \frac{3x}{4} - 4 \right)^{2} = 4 \Leftrightarrow x = \frac{16}{5}$ $\Leftrightarrow (x - 2)^{2} + \left( \frac{3x}{4} - 4 \right)^{2} = 4 \Leftrightarrow x = \frac{16}{5}$

$\Rightarrow y = - \frac{13}{5} \Rightarrow N\left( \frac{16}{5}; - \frac{13}{5};0 \right)$ $\Rightarrow y = - \frac{13}{5} \Rightarrow N\left( \frac{16}{5}; - \frac{13}{5};0 \right)$

Vậy $x_{N} + y_{N} = \frac{3}{5}$ $x_{N} + y_{N} = \frac{3}{5}$

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-----------------------------------------------------------------------------

Với bộ trắc nghiệm đúng sai phương trình mặt cầu trong không gian Oxyz có đáp án, học sinh không chỉ ôn lại lý thuyết trọng tâm mà còn nâng cao kỹ năng giải nhanh các dạng bài trắc nghiệm. Hãy luyện tập thường xuyên và kết hợp với các chuyên đề hình học không gian Toán 12 khác như đường thẳng, mặt phẳng, khoảng cách và góc để đạt kết quả cao nhất trong kỳ thi THPT Quốc gia.

Tải về

Chọn file muốn tải về: