Hướng dẫn tìm ẩn A, B, C trong bài toán tích phân bằng máy tính casio
Bạn đang gặp khó khăn khi giải các bài toán tích phân có chứa ẩn số A, B, C trong chương trình Toán lớp 12? Bài viết này sẽ hướng dẫn bạn cách tìm A, B, C trong tích phân bằng máy tính Casio một cách nhanh chóng, chính xác và dễ hiểu. Từ phương pháp tư duy đến mẹo bấm máy Casio 570VN Plus, bạn sẽ làm chủ dạng toán thường gặp trong đề thi THPT Quốc gia này chỉ sau vài bước đơn giản!
Bấm máy tính casio tìm A, B, C trong tích phân
Với những cải tiến đáng kể của chức năng lập bảng (TABLE) khi cho phép đưa phép tính tích phân vào trong các hàm ![]() \(f(x),g(x)\) để lập bảng giá trị. So với các dòng CASIO fx-570VN Plus trở về trước thì việc sử dụng chức năng bảng tính trong máy tính CASIO fx-580VN X để xác định các ẩn số trong các bài toán tích phân phức tạp trở nên đơn giản hơn khi chúng ta không phải tính tích phân rồi lưu vào ô nhớ trước khi sử dụng chức năng lập bảng. Dưới đây là một số bài cụ thể:
\(f(x),g(x)\) để lập bảng giá trị. So với các dòng CASIO fx-570VN Plus trở về trước thì việc sử dụng chức năng bảng tính trong máy tính CASIO fx-580VN X để xác định các ẩn số trong các bài toán tích phân phức tạp trở nên đơn giản hơn khi chúng ta không phải tính tích phân rồi lưu vào ô nhớ trước khi sử dụng chức năng lập bảng. Dưới đây là một số bài cụ thể:
Bài toán 3.1: Cho ![]() \(\int_{1}^{2}{\frac{1 -
x}{x^{2}}e^{x}dx} = ae^{2} + be\) với
\(\int_{1}^{2}{\frac{1 -
x}{x^{2}}e^{x}dx} = ae^{2} + be\) với ![]() \(a,b\mathbb{\in Q}\) . Tính
\(a,b\mathbb{\in Q}\) . Tính ![]() \(2a + 3b\)?
\(2a + 3b\)?
![]() \(S = \frac{1}{2}\) B.
\(S = \frac{1}{2}\) B.![]() \(S = 2\) C.
\(S = 2\) C. ![]() \(S =
\frac{5}{2}\) D.
\(S =
\frac{5}{2}\) D.![]() \(S =
\frac{7}{2}\)
\(S =
\frac{7}{2}\)
Hướng dẫn giải
Ta có : ![]() \(\int_{1}^{2}{\frac{1 -
x}{x^{2}}e^{x}dx} = ae^{2} + be\) suy ra
\(\int_{1}^{2}{\frac{1 -
x}{x^{2}}e^{x}dx} = ae^{2} + be\) suy ra  \(a = \frac{\int_{1}^{2}{\frac{1 - x}{x^{2}}e^{x}dx}
- be}{e^{2}}\)
\(a = \frac{\int_{1}^{2}{\frac{1 - x}{x^{2}}e^{x}dx}
- be}{e^{2}}\)
Cách 1: Sử dụng chức năng TABLE w8 để tìm giá trị a, b thích hợp
|
Nhập vào máy hàm số (có thể bỏ qua bước nhập |
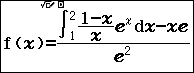 |
| Nhập |
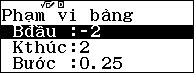 |
| Quan sát bảng kết quả ta chọn |
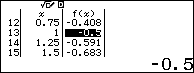 |
Vậy ![]() \(S = 2a + 3b =
2\)
\(S = 2a + 3b =
2\)
Cách 2: Giải hệ phương trình
Bên cạnh việc sử dụng chức năng bảng tính, chúng ta còn có thể sử dụng hệ phương trình để giải cho bài toán trên
Tiếp tục là một cải tiến mới của CASIO fx-580VN so với các dòng CASIO fx-570VN Plus. Ở phiên bản mới này ta có thể nhập tích phân ngay trên các hệ số, điều mà các dòng máy tiền nhiệm chưa làm được.
Đáp án A \(\left\{ \begin{matrix}
ae^{2} + be = \int_{1}^{2}{\frac{1 - x}{x^{2}}e^{x}dx} \\
2a + 3b = \frac{1}{2} \\
\end{matrix} \right.\) \(\left\{ \begin{matrix}
ae^{2} + be = \int_{1}^{2}{\frac{1 - x}{x^{2}}e^{x}dx} \\
2a + 3b = \frac{1}{2} \\
\end{matrix} \right.\) |
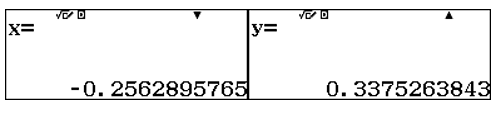 |
LOẠI (vì |
Đáp án B \(\left\{ \begin{matrix}
ae^{2} + be = \int_{1}^{2}{\frac{1 - x}{x^{2}}e^{x}dx} \\
2a + 3b = 2 \\
\end{matrix} \right.\) \(\left\{ \begin{matrix}
ae^{2} + be = \int_{1}^{2}{\frac{1 - x}{x^{2}}e^{x}dx} \\
2a + 3b = 2 \\
\end{matrix} \right.\) |
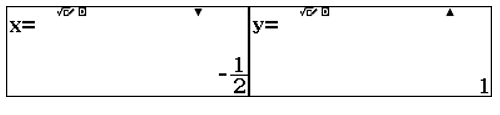 |
NHẬN |
Bài toán 3.2: Cho ![]() \(I =
\int_{1}^{e}{\frac{2lnx + 1}{x\left( \ln x + 1 \right)^{2}}dx} = aln2 -
\frac{b}{c}\left( a,b,c\mathbb{\in Z} \right)\) và
\(I =
\int_{1}^{e}{\frac{2lnx + 1}{x\left( \ln x + 1 \right)^{2}}dx} = aln2 -
\frac{b}{c}\left( a,b,c\mathbb{\in Z} \right)\) và ![]() \(\frac{b}{c}\) tối giản. Tính
\(\frac{b}{c}\) tối giản. Tính ![]() \(S = a + b + c\).
\(S = a + b + c\).
A. ![]() \(S = 0\) B.
\(S = 0\) B. ![]() \(S = 3\) C.
\(S = 3\) C.![]() \(S =
5\) D.
\(S =
5\) D. ![]() \(S = 7\)
\(S = 7\)
Hướng dẫn giải
Đặt ![]() \(d = \frac{b}{c}\). Khi đó
\(d = \frac{b}{c}\). Khi đó ![]() \(d = aln2 - \int_{1}^{e}{\frac{2lnx +
1}{x(lnx + 1)^{2}}dx}\)
\(d = aln2 - \int_{1}^{e}{\frac{2lnx +
1}{x(lnx + 1)^{2}}dx}\)
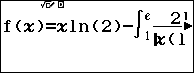
Sử dụng chức năng TABLE để tìm giá trị a, d thích hợp
| Nhập vào máy hàm số |
 |
| Nhập |
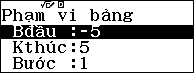 |
|
Quan sát bảng kết quả và dựa vào điều kiện Suy ra: |
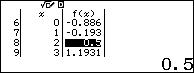 |
| Vây: |
Đáp án: C |
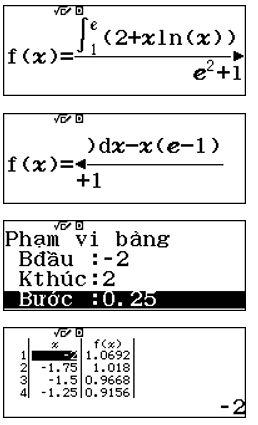
Bài toán 3.3 Cho tích phân ![]() \(\int_{1}^{e}{(2 + x\ln x)dx} = ae^{2} + be +
c\) (
\(\int_{1}^{e}{(2 + x\ln x)dx} = ae^{2} + be +
c\) (![]() \(a,b,c\) là số hữu tỉ). Xác định mệnh đề đúng
\(a,b,c\) là số hữu tỉ). Xác định mệnh đề đúng
A.![]() \(a + b = c\) B.
\(a + b = c\) B. ![]() \(a - b = c\) C.
\(a - b = c\) C. ![]() \(a - b = - c\) D.
\(a - b = - c\) D.![]() \(a + b = - c\)
\(a + b = - c\)
Hướng dẫn giải
Sử dụng chức năng TABLE w8 kiểm tra các đáp án
|
Đáp A: Suy ra Nhập vào máy hàm số Nhập Quan sát bảng giá trị ta thấy tất cả các giá trị |
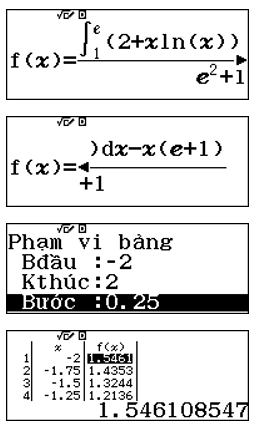 |
|
Đáp án B: Suy ra Nhập vào máy hàm số Nhập Quan sát bảng giá trị ta thấy ta thấy tồn tại Do đó ta chọn đáp án B |
|
Bình luận: Để chọn Bắt đầu (Start), Kết thúc (End) và Bước (Step) thích hợp, chúng ta nên xem xét phân tích kĩ điều kiện của các ẩn số kết hợp với các đáp án trong đề bài ( Ví dụ: ![]() \(a,b,c\mathbb{\in N},\mathbb{Z}\) thì ta chọn
\(a,b,c\mathbb{\in N},\mathbb{Z}\) thì ta chọn ![]() \(Step = 1\);
\(Step = 1\); ![]() \(a,b,c\mathbb{\in Q}\) thì thường chọn
\(a,b,c\mathbb{\in Q}\) thì thường chọn ![]() \(Step =
\frac{1}{5};\frac{1}{4};\frac{1}{2};...\) )
\(Step =
\frac{1}{5};\frac{1}{4};\frac{1}{2};...\) )
----------------------------------------------
Trên đây là toàn bộ hướng dẫn chi tiết về cách tìm ẩn số A, B, C trong bài toán tích phân bằng máy tính Casio. Hy vọng sau bài viết, bạn đã nắm vững phương pháp, hiểu rõ tư duy giải và tự tin áp dụng trong mọi dạng đề. Đừng quên luyện tập thường xuyên với các bài tập có tham số để thành thạo kỹ năng này. Chúc bạn học tốt và đạt điểm cao trong các kỳ thi!