™
Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12

Tìm vecto chỉ phương của đường thẳng trong không gian Oxyz

Chuyên đề Toán 12 Phương trình đường thẳng
Tải về

Cách xác định vectơ chỉ phương

Trong hình học không gian Oxyz, vectơ chỉ phương của đường thẳng đóng vai trò quan trọng giúp xác định phương của đường thẳng và viết phương trình tham số. Tuy nhiên, không ít học sinh còn lúng túng khi cần tìm vectơ chỉ phương từ các dữ kiện đề bài. Bài viết dưới đây sẽ giúp bạn hiểu rõ vectơ chỉ phương là gì, cách xác định vectơ này trong từng trường hợp cụ thể, kèm ví dụ minh họa chi tiết và dễ hiểu.

A. Vectơ chỉ phương là gì?

Cho đường thẳng ∆. Vectơ \overrightarrow{u} \neq \overrightarrow{0}u→≠0→ gọi là vectơ chỉ phương của đường thẳng ∆ nếu giá của nó song song hoặc trùng với ∆.

Cho đường thẳng ∆ đi qua M\left( x_{0};y_{0};z_{0} \right)M(x0;y0;z0) và có vectơ chỉ phương là \overrightarrow{u} = (a;b;c)u→=(a;b;c).

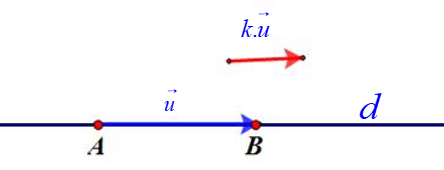
Chú ý:

  • Nếu \overrightarrow{u}u→ là vectơ chỉ phương của ∆ thì k.\overrightarrow{u}(k \neq 0)k.u→(k≠0) cũng là vectơ chỉ phương của ∆.
  • Nếu đường thẳng ∆ đi qua hai điểm A, B thì \overrightarrow{AB}AB→ là một vectơ chỉ phương.
  • Cho đường thẳng ∆ có phương trình (1) thì
  • \overrightarrow{u} = (a;b;c)u→=(a;b;c) là một vectơ chỉ phương của ∆.
  • Với điểm M \in \DeltaM∈Δ thì M\left( x_{0} + at;y_{0} + bt;z_{0} + ct \right)M(x0+at;y0+bt;z0+ct) trong đó t là một giá trị cụ thể tương ứng với từng điểm  

B. Phương trình tham số của đường thẳng

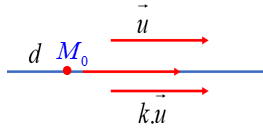
Phương trình tham số của đường thẳng \DeltaΔ đi qua điểm M0(x0; y0; z0) và có vectơ chỉ phương \overrightarrow{a} = (a_{1};a_{2};a_{3})a→=(a1;a2;a3) ,\overrightarrow{a} \neq \overrightarrow{0}a→≠0→ :

\left\{ \begin{matrix} x = x_{0} + a_{1}t \\ y = y_{0} + a_{2}t \\ z = z_{0} + a_{3}t \\ \end{matrix} \right.\ \ \ \ \ \ \ (t \in R){x=x0+a1ty=y0+a2tz=z0+a3t       (t∈R)

C. Phương trình chính tắc của đường thẳng

Nếu a1, a2, a3 đều khác không. Phương trình đường thẳng\DeltaΔ viết dưới dạng chính tắc như sau:

\frac{x - x_{0}}{a_{1}} = \frac{y - y_{0}}{a_{2}} = \frac{z - z_{0}}{a_{3}}x−x0a1=y−y0a2=z−z0a3

Chú ý: Cần xác định 1 điểm và 1 vecto chỉ phương để viết phương trình tham số của đường thẳng.

D. Bài tập tìm vectơ chỉ phương của đường thẳng trong không gian

Câu 1: Trong không gian Oxyz, một vectơ chỉ phương của đường thẳng d: \frac{x - 1}{1} = \frac{y + 2}{- 1} = \frac{z}{2}x−11=y+2−1=z2 là

A. \overrightarrow{u} = (1; - 1;2)u→=(1;−1;2) B. \overrightarrow{u} = (1;1;2)u→=(1;1;2) C. \overrightarrow{u} = (1; - 2;0)u→=(1;−2;0) D. \overrightarrow{u} = (1; - 2;1)u→=(1;−2;1)

Hướng dẫn giải

Một vectơ chỉ phương của đường thẳng d là \overrightarrow{u} = (1; - 1;2)u→=(1;−1;2).

Chọn A

Câu 2: Trong không gian với hệ toạ độ OxyzOxyz, cho đường thẳng d:\ \frac{x - 2}{2} = \frac{y + 1}{- 1} = \frac{z - 1}{- 1}d: x−22=y+1−1=z−1−1. Phương trình tham số của đường thẳng dd là?

A. \left\{ \begin{matrix} x = 2 - 2t \\ y = 1 - t \\ z = - 1 - t \\ \end{matrix} \right.{x=2−2ty=1−tz=−1−t, \left( t \in \mathbb{R} \right)(t∈R).                                B. \left\{ \begin{matrix} x = 2 + 2t \\ y = - 1 - t \\ z = 1 - t \\ \end{matrix} \right.{x=2+2ty=−1−tz=1−t, \left( t \in \mathbb{R} \right)(t∈R).

C. \left\{ \begin{matrix} x = 2 + 2t \\ y = - 1 - t \\ z = - 1 + t \\ \end{matrix} \right.{x=2+2ty=−1−tz=−1+t, \left( t \in \mathbb{R} \right)(t∈R).                               D. \left\{ \begin{matrix} x = 2 + 2t \\ y = - 1 - t \\ z = - 1 - t \\ \end{matrix} \right.{x=2+2ty=−1−tz=−1−t, \left( t \in \mathbb{R} \right)(t∈R).

Hướng dẫn giải

Đường thẳng dd qua A(2; - 1;\ 1)A(2;−1; 1) có VTCP \overrightarrow{u_{d}} = (2;\ - 1;\ - 1)ud→=(2; −1; −1)

Phương trình tham số của d:\ \left\{ \begin{matrix} x = 2 + 2t \\ y = - 1 - t \\ z = 1 - t \\ \end{matrix} \right.d: {x=2+2ty=−1−tz=1−t, \left( t \in \mathbb{R} \right)(t∈R).

Chọn B

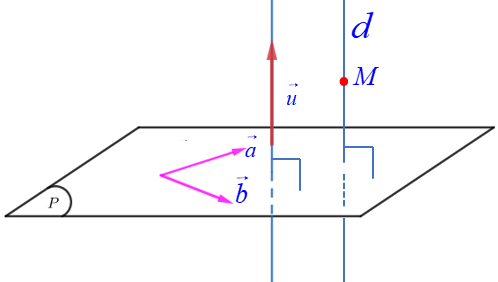
Câu 3: Trong không gian OxyzOxyz, cho mặt phẳng (P):x - 2y - 3z - 2 = 0(P):x−2y−3z−2=0. Đường thẳng dd vuông góc với mặt phẳng (P)(P) có một vectơ chỉ phương là

A. \overrightarrow{u_{1}} = (1; - 2; - 2)u1→=(1;−2;−2)                                           B. \overrightarrow{u_{2}} = (1; - 2; - 3)u2→=(1;−2;−3)

C. \overrightarrow{u_{4}} = (1;2;3)u4→=(1;2;3)                                                 D. \overrightarrow{u_{3}} = (1; - 3; - 2)u3→=(1;−3;−2)

Hướng dẫn giải

Ta có (P):x - 2y - 3z - 2 = 0(P):x−2y−3z−2=0, suy ra một VTPT của (P)(P) là \overrightarrow{u_{2}} = (1; - 2; - 3)u2→=(1;−2;−3).

Chọn B

Câu 4: Trong không gian với hệ tọa độ OxyzOxyz vectơ nào dưới đây là vectơ chỉ phương của OzOz?

A. \overrightarrow{j\ } = (0;1;0)j →=(0;1;0).              B. \overrightarrow{i\ } = (1;0;0)i →=(1;0;0).               C. \overrightarrow{m\ } = (1;1;1)m →=(1;1;1).              D. \overrightarrow{k\ } = (0;0;1)k →=(0;0;1).

Hướng dẫn giải

Trục OzOz có một vectơ chỉ phương là \overrightarrow{k\ } = (0;0;1)k →=(0;0;1).

Chọn D

-----------------------------------------------------------------------

Qua bài viết, bạn đã nắm được cách tìm vectơ chỉ phương của đường thẳng trong không gian Oxyz một cách dễ hiểu và chính xác. Đây là nền tảng quan trọng để viết phương trình đường thẳng, giải các bài toán hình học không gian nâng cao. Hãy luyện tập thường xuyên với các ví dụ và bài tập tương tự để thành thạo hơn. Đừng quên lưu lại bài viết để ôn tập khi cần nhé!

Chia sẻ, đánh giá bài viết
1
10 Bài viết đã được lưu
Mục lục
Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!
Đóng
79.000 / tháng
Mua ngay
Đặc quyền các gói Thành viên
PRO
Phổ biến nhất
PRO+
Tải tài liệu Cao cấp 1 Lớp
Tải tài liệu Trả phí + Miễn phí
Xem nội dung bài viết
Trải nghiệm Không quảng cáo
Làm bài trắc nghiệm không giới hạn
Mua cả năm Tiết kiệm tới 48%
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này

Nhiều người đang xem

Tham khảo thêm

🖼️

Gợi ý cho bạn
Xem thêm
🖼️

Chuyên đề Toán 12
Xem thêm
Chia sẻ
Chia sẻ FacebookChia sẻ TwitterSao chép liên kếtQuét bằng QR Code
Mã QR Code
Đóng