Giải Toán 12 trang 13 tập 1 Kết nối tri thức
Giải Toán 12 trang 13 Tập 1
Giải Toán 12 trang 13 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 13.
Bài 1.1 trang 13 SGK Toán 12 tập 1 KNTT
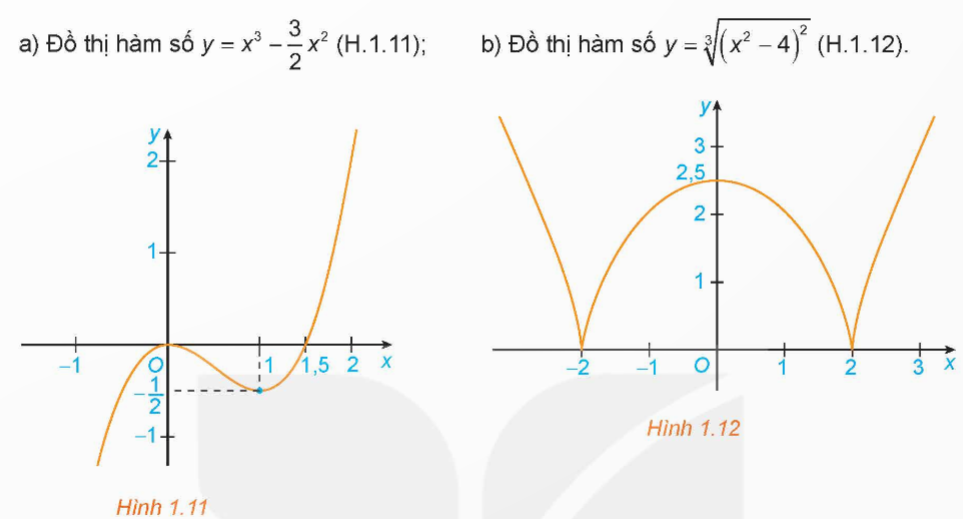
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
Hướng dẫn giải:
a) Tập xác định của hàm số là R.
Từ đồ thị hàm số Hình 1.11 suy ra:
- Hàm số đồng biến trên khoảng (− ∞; 0) và (1; + ∞)
- Hàm số nghịch biến trên khoảng (0; 1)
b) Tập xác định của hàm số là R.
Từ đồ thị hàm số Hình 1.12 suy ra:
- Hàm số đồng biến trên khoảng (− 2; 0) và (2; + ∞)
- Hàm số nghịch biến trên khoảng (- ∞; − 2) và (0; 2).
Bài 1.2 trang 13 SGK Toán 12 tập 1 KNTT
Xét sự đồng biến, nghịch biến của hàm số sau:
a) 
\(y=\frac{1}{3}x^3-2x^2+3x+1\)
b) y = − x3 + 2x2 − 5x + 3.
Hướng dẫn giải:
a) \(y=\frac{1}{3}x^3-2x^2+3x+1\)
Tập xác định của hàm số là R.
Ta có: y' = x2 − 4x + 3
y' = 0 \(\Leftrightarrow\) x = 1 hoặc x = 3.
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left(-∞;1\right)\) và \(\left(3;+∞\right)\)
Hàm số nghịch biến trên các khoảng (1; 3).
b) y = − x3 + 2x2 − 5x + 3.
Tập xác định của hàm số là R.
Ta có: y' = − 3x2 + 4x − 5
= \(-3\left(x^2-\frac{4}{3}x+\frac{5}{3}\right)\)
\(=-3\left(x-\frac{2}{3}\right)^2-\frac{11}{3} <0\) với mọi x
Hàm số nghịch biến trên R.
Bài 1.3 trang 13 SGK Toán 12 tập 1 KNTT
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y=\frac{2x-1}{x+2}\)
b) \(y=\frac{x^2+x+4}{x-3}\)
Hướng dẫn giải:
a) \(y=\frac{2x-1}{x+2}\)
Tập xác định của hàm số là R \ {− 2}
Ta có: \(y'=\frac{2\left(x+2\right)-\left(2x-1\right)}{\left(x+2\right)^2}=\frac{5}{\left(x+2\right)^2} >0\), với mọi x ≠ − 2.
Lập bảng biến thiên của hàm số:
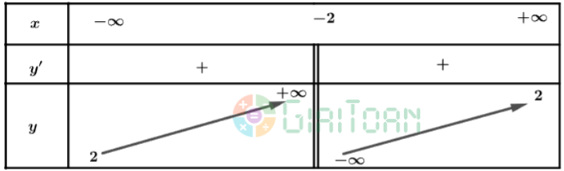
Từ bảng biến thiên, ta có: Hàm số đồng biến trên các khoảng \(\left(-∞;-2\right)\) và \(\left(-2;+∞\right)\)
b) \(y=\frac{x^2+x+4}{x-3}\)
Tập xác định của hàm số là R \ {3}
Ta có: \(y'=\frac{(2x+1)\left(x-3\right)-\left(x^2+x+4\right)}{\left(x-3\right)^2}=\frac{x^2-6x-7}{\left(x-3\right)^2}\)
y' = 0 \(\Leftrightarrow\) x= − 1 hoặc x = 7
Lập bảng biến thiên của hàm số:
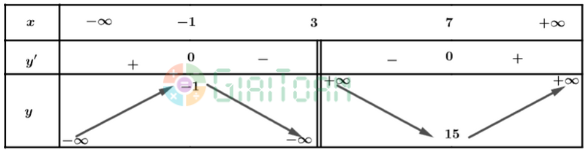
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left(-∞;-1\right)\) và \(\left(7;+∞\right)\)
Hàm số nghịch biến trên các khoảng (− 1; 3) và (3; 7)
Bài 1.4 trang 13 SGK Toán 12 tập 1 KNTT
Xét chiều biến thiên của các hàm số sau:
a) \(y=\sqrt{4-x^2}\)
b) \(y=\frac{x}{x^2+1}\)
Hướng dẫn giải:
a) \(y=\frac{2x-1}{x+2}\)
Tập xác định của hàm số là R \ {- 2}
Ta có: \(y'=\frac{2\left(x+2\right)-\left(2x-1\right)}{\left(x+2\right)^2}=\frac{5}{\left(x+2\right)^2} >0\), với mọi x ≠ - 2.
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có: Hàm số đồng biến trên các khoảng \(\left(-∞;-2\right)\) và \(\left(-2;+∞\right)\)
b) \(y=\frac{x^2+x+4}{x-3}\)
Tập xác định của hàm số là R \ {3}
Ta có: \(y'=\frac{(2x+1)\left(x-3\right)-\left(x^2+x+4\right)}{\left(x-3\right)^2}=\frac{x^2-6x-7}{\left(x-3\right)^2}\)
y' = 0 \(\Leftrightarrow\) x= - 1 hoặc x = 7
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left(-∞;-1\right)\) và \(\left(7;+∞\right)\)
Hàm số nghịch biến trên các khoảng (- 1; 3) và (3; 7)
Bài 1.5 trang 13 SGK Toán 12 tập 1 KNTT
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số
\(N\left(t\right)=\frac{25t+10}{t+5},\ t\ge0,\)
trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N'(t) và \(\lim_{t\rightarrow +\infty} N(t)\). Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Hướng dẫn giải:
a) Số dân của thị trấn đó vào năm 2000, tức t = 0 là:
\(N\left(0\right)=\frac{25.0+10}{0+5}=2\) (nghìn người)
Số dân của thị trấn đó vào năm 2015, tức t = 15 là:
\(N\left(15\right)=\frac{25.15+10}{15+5}=19,25\) (nghìn người)
b) Ta có \(N'\left(t\right)=\frac{25\left(t+5\right)-\left(25t+10\right)}{\left(t+5\right)^2}=\frac{115}{\left(t+5\right)^2} >0\) với mọi t.
\(\lim_{t\rightarrow +\infty} N(t) = \lim_{t\rightarrow +\infty} \frac{25t+10}{t+5}=25\)
Do đó số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá 25 nghìn người.
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 14 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 13 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 1 Tính đơn điệu và cực trị của hàm số, được VnDoc biên soạn và đăng tải!
