VnDoc.com

Giải Toán 12 trang 19 tập 1 Kết nối tri thức

Bài trước

Bài sau

Giải Toán 12 trang 19 Tập 1

Bài 1.10 trang 19 SGK Toán 12 tập 1 Kết nối
Bài 1.11 trang 19 SGK Toán 12 tập 1 Kết nối
Bài 1.12 trang 19 SGK Toán 12 tập 1 Kết nối
Bài 1.13 trang 19 SGK Toán 12 tập 1 Kết nối
Bài 1.14 trang 19 SGK Toán 12 tập 1 Kết nối
Bài 1.15 trang 19 SGK Toán 12 tập 1 Kết nối

Giải Toán 12 trang 19 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 19.

Bài 1.10 trang 19 SGK Toán 12 tập 1 Kết nối

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = - {x^2} + 4x + 3$ $y = - {x^2} + 4x + 3$;

b) $y = {x^3} - 2{x^2} + 1$ $y = {x^3} - 2{x^2} + 1$ trên $\left[ {0; + \infty } \right)$ $\left[ {0; + \infty } \right)$;

c) $y = \frac{{{x^2} - 2x + 3}}{{x - 1}}$ $y = \frac{{{x^2} - 2x + 3}}{{x - 1}}$ trên $\left( {1; + \infty } \right)$ $\left( {1; + \infty } \right)$;

d) $y = \sqrt {4x - 2{x^2}}$ $y = \sqrt {4x - 2{x^2}}$.

Hướng dẫn giải:

a) y = - x² + 4x + 3

Tập xác định của hàm số là: R

Ta có: y' = - 2x + 4; y' = 0 ⇔ x = 2

Lập bảng biến thiên của hàm số:

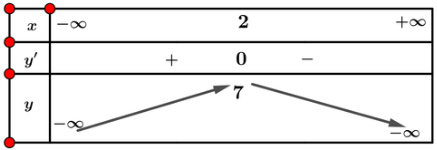
Từ bảng biến thiên ta được: $\underset{\mathbb{R}}{\max} y = 7$ $\underset{\mathbb{R}}{\max} y = 7$, hàm số không có giá trị nhỏ nhất.

b) y = x³ - 2x² + 1 trên [0; + ∞)

Ta có: y' = 3x² - 4x = x(3x - 4)

y' = 0 ⇔ x = 0 hoặc x = $\frac{4}{3}$ $\frac{4}{3}$ (vì x ∈ [0; + ∞))

Lập bảng biến thiên của hàm số trên [0; + ∞):

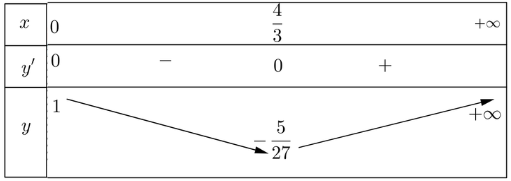
Từ bảng biến thiên, ta được: $\underset{[0; + ∞)}{\min} y = - \frac{5}{27}$ $\underset{[0; + ∞)}{\min} y = - \frac{5}{27}$, hàm số không có giá trị lớn nhất.

c) $y=\frac{x^2-2x+3}{x-1}$ $y=\frac{x^2-2x+3}{x-1}$ trên (1; + ∞)

Ta có: $y'=\frac{x^2-2x-1}{\left(x-1\right)^2}$

y' = 0 ⇔ $x=\sqrt{2}+1$ $x=\sqrt{2}+1$ (vì x ∈ (1; + ∞))

Lập bảng biến thiên của hàm số trên (1; + ∞):

Từ bảng biến thiên, ta được: $\underset{(1; + ∞)}{\min} y = 2\sqrt{2}$ $\underset{(1; + ∞)}{\min} y = 2\sqrt{2}$, hàm số không có giá trị lớn nhất.

d) $y=\sqrt{4x-2x^2}$ $y=\sqrt{4x-2x^2}$

TXĐ: [0; 2]

Ta có: $y'=\frac{2-2x}{\sqrt{4x-2x^2}}$

y' = 0 ⇔ x = 1

y(0) = 0; y(1) = $\sqrt{2}$ $\sqrt{2}$; y(2) = 0

Vậy $\underset{[0;2]}{\max} y = \sqrt{2} ; \ \underset{[0;2]}{\min} y = 0$ $\underset{[0;2]}{\max} y = \sqrt{2} ; \ \underset{[0;2]}{\min} y = 0$.

Bài 1.11 trang 19 SGK Toán 12 tập 1 Kết nối

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) y = x⁴ – 2x² + 3

b) y = xe^−x

c) y = xlnx

d) $y = \sqrt{x - 1} + \sqrt{3 - x}$ $y = \sqrt{x - 1} + \sqrt{3 - x}$

Hướng dẫn giải:

a) y = x⁴ - 2x² + 3

Tập xác định của hàm số là: R

Ta có: y' = 4x³ - 4x = 4x(x - 1)(x + 1)

y' = 0 ⇔ $\left [ \begin{array}{l} x= - 1 \\ x = 0 \\ x = 1 \end{array} \right.$ $\left [ \begin{array}{l} x= - 1 \\ x = 0 \\ x = 1 \end{array} \right.$

Lập bảng biến thiên của hàm số:

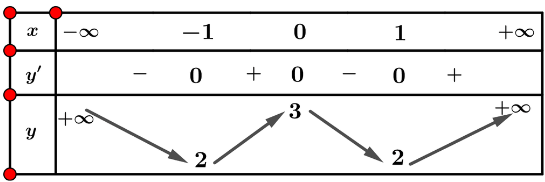
Từ bảng biến thiên ta được: $\underset{\mathbb{R}}{\max} y = 3,\ \underset{\mathbb{R}}{\min} y = 2$ $\underset{\mathbb{R}}{\max} y = 3,\ \underset{\mathbb{R}}{\min} y = 2$.

b) y = xe^{- x}

Tập xác định của hàm số là: R

Ta có: $y'=\frac{1-x}{e^x}$; y' = 0 ⇔ x = 1

Lập bảng biến thiên của hàm số:

Từ bảng biến thiên, ta được: $\underset{R}{\max} y = \frac{1}{e}$ $\underset{R}{\max} y = \frac{1}{e}$, hàm số không có giá trị nhỏ nhất.

c) $y=x \ln x$ $y=x \ln x$

Tập xác định của hàm số là: (0; + ∞)

Ta có: y' = ln x + 1; y' = 0 ⇔ $x=\frac{1}{e}$ $x=\frac{1}{e}$

Lập bảng biến thiên của hàm số trên (0; + ∞):

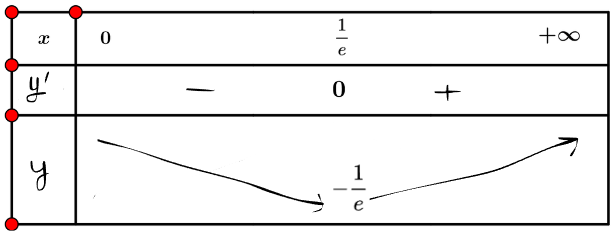
Từ bảng biến thiên, ta được: $\underset{R}{\min} y = -\frac{1}{e}$ $\underset{R}{\min} y = -\frac{1}{e}$, hàm số không có giá trị lớn nhất.

d) $y=\sqrt{x-1} +\sqrt{3-x}$ $y=\sqrt{x-1} +\sqrt{3-x}$

Tập xác định của hàm số là: [1; 3]

Ta có: $y'=\frac{1}{2\sqrt{x-1}}+\frac{1}{2\sqrt{3-x}}$

y' = 0 ⇔ x = 2

$y\left(1\right)=\sqrt{2};\ y\left(2\right)=2;\ y\left(3\right)=\sqrt{2}$ $y\left(1\right)=\sqrt{2};\ y\left(2\right)=2;\ y\left(3\right)=\sqrt{2}$

Từ bảng biến thiên, ta được: $\underset{[1;3]}{\max} y = 2, \ \underset{[1;3]}{\min} y = \sqrt{2}$ $\underset{[1;3]}{\max} y = 2, \ \underset{[1;3]}{\min} y = \sqrt{2}$.

Bài 1.12 trang 19 SGK Toán 12 tập 1 Kết nối

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = 2{x^3} - 6x + 3$ $y = 2{x^3} - 6x + 3$ trên đoạn $\left[ { - 1;2} \right]$ $\left[ { - 1;2} \right]$

b) $y = {x^4} - 3{x^2} + 2$ $y = {x^4} - 3{x^2} + 2$ trên đoạn $\left[ {0;3} \right]$ $\left[ {0;3} \right]$

c) $y = x - \sin 2x$ $y = x - \sin 2x$ trên đoạn $\left[ {0;\pi } \right]$ $\left[ {0;\pi } \right]$

d) $y = \left( {{x^2} - x} \right){e^x}$ $y = \left( {{x^2} - x} \right){e^x}$ trên đoạn $\left[ {0;1} \right]$ $\left[ {0;1} \right]$

Hướng dẫn giải:

a) y = 2x³ – 6x + 3

Ta có: y' = 6x² – 6 = 6(x – 1)(x + 1)

y' = 0 ⇔ $\left [ \begin{array}{l} x= - 1 \\ x = 1 \end{array} \right.$ $\left [ \begin{array}{l} x= - 1 \\ x = 1 \end{array} \right.$

y(– 1) = 7; y(1) = – 1; y(2) = 7

Do đó: $\underset{[- 1; 2]}{\max} y = 7,\ \underset{[- 1; 2]}{\min} y = -1$ $\underset{[- 1; 2]}{\max} y = 7,\ \underset{[- 1; 2]}{\min} y = -1$.

b) y = x⁴ – 3x² + 2

Ta có: y' = 4x³ – 6x = 2x(x² – 3)

y' = 0 ⇔ $\left [ \begin{array}{l} x= 0 \\ x = \frac{\sqrt{6} }{ 2} \end{array} \right.$ $\left [ \begin{array}{l} x= 0 \\ x = \frac{\sqrt{6} }{ 2} \end{array} \right.$

$y\left(0\right)=2;\ y\left(\frac{\sqrt{6}}{2}\right)=-\frac{1}{4};\ y\left(3\right)=56$ $y\left(0\right)=2;\ y\left(\frac{\sqrt{6}}{2}\right)=-\frac{1}{4};\ y\left(3\right)=56$

Do đó: $\underset{[0 ; 3]}{\max} y = 56,\ \underset{[0; 3]}{\min} y = -\frac{1}{4}$ $\underset{[0 ; 3]}{\max} y = 56,\ \underset{[0; 3]}{\min} y = -\frac{1}{4}$.

c) y = x – sin2x

Ta có: y' = 1 – 2cos2x

y' = 0 ⇔ $x=\frac{\pi}{6}$ $x=\frac{\pi}{6}$ (vì x ∈ [0; π])

$y\left(0\right)=0; \ y\left(\pi\right)=\pi$ $y\left(0\right)=0; \ y\left(\pi\right)=\pi$

$y\left(\frac{\pi}{6}\right)=\frac{\pi-3\sqrt{3}}{6}; \ y\left(\frac{5\pi}{6}\right)=\frac{5\pi+3\sqrt{3}}{6};$ $y\left(\frac{\pi}{6}\right)=\frac{\pi-3\sqrt{3}}{6}; \ y\left(\frac{5\pi}{6}\right)=\frac{5\pi+3\sqrt{3}}{6};$

Do đó: $\underset{[0 ; π]}{\max} y = \frac{5\pi+3\sqrt{3}}{6}$ $\underset{[0 ; π]}{\max} y = \frac{5\pi+3\sqrt{3}}{6}$

$\underset{[0; π]}{\min} y = \frac{π-3\sqrt{3} }{6}$ $\underset{[0; π]}{\min} y = \frac{π-3\sqrt{3} }{6}$

d) y = (x² – x)e^x

Ta có: y' = e^x(x² + x – 1)

y' = 0 ⇔ $x=\frac{\sqrt{5}-1}{2}$ $x=\frac{\sqrt{5}-1}{2}$

$y\left(0\right)=0 ;\ y\left(1\right)=0$ $y\left(0\right)=0 ;\ y\left(1\right)=0$

$y\left(\frac{\sqrt{5}-1}{2}\right)=\left(2-\sqrt{5}\right)e^{\frac{\sqrt{5}-1}{2}}$ $y\left(\frac{\sqrt{5}-1}{2}\right)=\left(2-\sqrt{5}\right)e^{\frac{\sqrt{5}-1}{2}}$

Do đó: $\underset{[0 ; 1]}{\max} y =0$ $\underset{[0 ; 1]}{\max} y =0$

$\underset{[0; 1]}{\min} y = \left(2-\sqrt{5}\right)e^{\frac{\sqrt{5}-1}{2}}$ $\underset{[0; 1]}{\min} y = \left(2-\sqrt{5}\right)e^{\frac{\sqrt{5}-1}{2}}$

Bài 1.13 trang 19 SGK Toán 12 tập 1 Kết nối

Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Hướng dẫn giải:

Nửa chu vi: 24 : 2 = 12 cm

Gọi chiều dài là x (cm), chiều rộng là 12 – x (cm) (0 < x < 12)

Gọi S(x) là hàm số biểu thị diện tích của hình chữ nhật, ta có:

S(x) = x(12 – x) = 12x – x², 0 < x < 12

Ta có: S'(x) = 12 – 2x; S'(x) = 0 ⇔ x = 6

Lập bảng biến thiên của hàm số S(x) trên (0; 12):

Từ bảng biến thiên, ta có $\underset{(0;12)}{\max} S(x) = 36$ $\underset{(0;12)}{\max} S(x) = 36$

Vậy hình chữ nhật có diện tích lớn nhất là 36 cm² (tức là khi chữ nhật trở thành hình vuông)

Bài 1.14 trang 19 SGK Toán 12 tập 1 Kết nối

Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108cm² như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

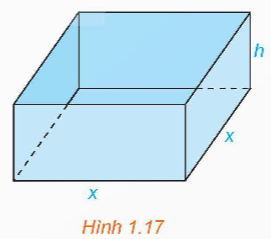
Hướng dẫn giải:

Diện tích bề mặt là: 4xh + x² = 108 (cm²)

⇒ $h=\frac{108-x^2}{4x}$ $h=\frac{108-x^2}{4x}$

Gọi V(x) là hàm số biểu thị thể tích của hình hộp chữ nhật, ta có:

$V(x)=S_{đáy}.h=\frac{x\left(108-x^2\right)}{4}=\frac{-x^3+108x}{4}$ $V(x)=S_{đáy}.h=\frac{x\left(108-x^2\right)}{4}=\frac{-x^3+108x}{4}$, x > 0

Ta có: $V'\left(x\right)=-\frac{3x^2}{4}+27$; V'(x) = 0 ⇔ x = 6 (do x > 0)

Lập bảng biến thiên của hàm số V(x) trên (0; + ∞):

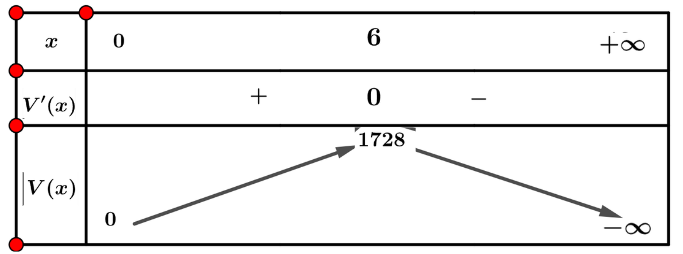
Từ bảng biến thiên, ta có $\underset{(0;+ \infty )}{\max}V(x) = 1728$ $\underset{(0;+ \infty )}{\max}V(x) = 1728$

Vậy để hình hộp có thể tích lớn nhất thì đáy có cạnh bằng 6 và chiều cao h = 3 cm.

Bài 1.15 trang 19 SGK Toán 12 tập 1 Kết nối

Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm³. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/cm², trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/cm². Tính các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.

Hướng dẫn giải:

Diện tích mặt đáy là: S_đáy = πR² (cm²)

Thể tích khối trụ là: V = πR²h = 1 000 (cm³)

=> Chiều cao khối trụ là: $h=\frac{1\ 000}{\pi R^2}$ $h=\frac{1\ 000}{\pi R^2}$ (cm)

Diện tích xung quanh khối trụ là: S_xq = 2πRh = $\frac{2000}{R}$ $\frac{2000}{R}$ (cm²)

Gọi C(R) là hàm số biểu thị chi phí vật liệu sản xuất mỗi chiếc bình, ta có:

$C\left(R\right)=2\pi R^2.1,2+\frac{2000}{R}.0,75=2,4\pi R^2+\frac{1500}{R}$ $C\left(R\right)=2\pi R^2.1,2+\frac{2000}{R}.0,75=2,4\pi R^2+\frac{1500}{R}$, R > 0

Ta có: $C'\left(R\right)=4,8\pi R-\frac{1500}{R^2}$; C'(x) = 0 ⇔ $R=\sqrt[3]{\frac{625}{2\pi}}$ $R=\sqrt[3]{\frac{625}{2\pi}}$ (do R > 0)

Lập bảng biến thiên của hàm số C'(R) trên (0; + ∞):

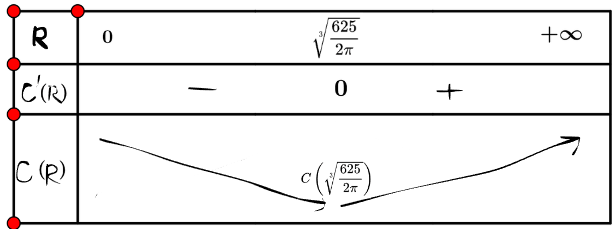
Vậy để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất thì bán kính đáy $R=\sqrt[3]{\frac{625}{2\pi}}$ $R=\sqrt[3]{\frac{625}{2\pi}}$

-----------------------------------------------

---> Bài tiếp theo: Toán 12 Kết nối tri thức bài 3: Đường tiệm cận của đồ thị hàm số

Lời giải Toán 12 trang 19 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

1.155

Bài trước

Bài sau