VnDoc.com

Giải Toán 12 trang 14 tập 1 Kết nối tri thức

Bài trước

Tải về

Bài sau

Giải Toán 12 trang 14 Tập 1

Bài 1.6 trang 14 SGK Toán 12 tập 1 KNTT
Bài 1.7 trang 14 SGK Toán 12 tập 1 KNTT
Bài 1.8 trang 14 SGK Toán 12 tập 1 KNTT
Bài 1.9 trang 14 SGK Toán 12 tập 1 KNTT

Giải Toán 12 trang 14 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 14.

Bài 1.6 trang 14 SGK Toán 12 tập 1 KNTT

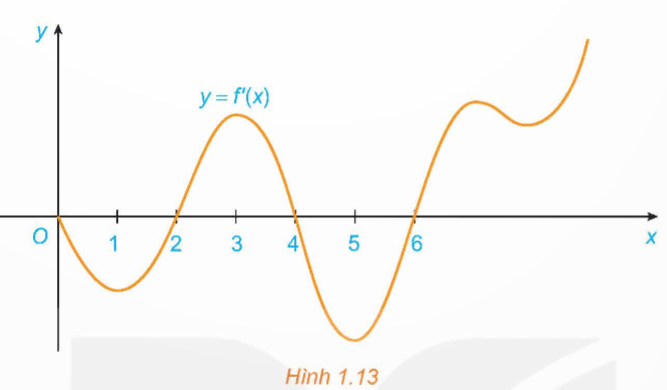
Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong Hình 1.13.

a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.

b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích?

Hướng dẫn giải:

a) Từ đồ thi của hàm số y = f'(x), ta có:

Hàm số đồng biến trên các khoảng (2; 4) và (6; + ∞)

Hàm số nghịch biến trên các khoảng (0; 2) và (4; 6)

b) Ta có:

f'(x) < 0 với mọi điểm x ∈ (0; 2) và f'(x) > 0 với mọi điểm x ∈ (0; 4) nên x = 2 là điểm cực tiểu.

f'(x) < 0 với mọi điểm x ∈ (4; 6) và f'(x) > 0 với mọi điểm x ∈ (6; + ∞) nên x = 6 là điểm cực tiểu.

f'(x) > 0 với mọi điểm x ∈ (2; 4) và f'(x) < 0 với mọi điểm x ∈ (4; 6) nên x = 4 là điểm cực đại.

Bài 1.7 trang 14 SGK Toán 12 tập 1 KNTT

Tìm cực trị của các hàm số sau:

a) y = 2x³ – 9x² + 12x – 5

b) y = x⁴ – 4x² + 2

c) $y=\frac{x^2-2x+3}{x-1}$ $y = \frac{x^{2} - 2 x + 3}{x - 1}$

d) $y=\sqrt{4x-2x^2}$ $y = \sqrt{4 x - 2 x^{2}}$

Hướng dẫn giải:

a) y = 2x³ – 9x² + 12x – 5

Tập xác định của hàm số là R.

Ta có: y' = 6x² – 18x + 12 = 6(x – 1)(x – 2)

y' = 0 $\Leftrightarrow$ $\Leftrightarrow$ x = 1 hoặc x = 2

Lập bảng biến thiên của hàm số:

Từ bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại x = 2 và y_CT = y(2) = – 1

Hàm số đạt cực đại tại x = 1 và y_CĐ = y(1) = 0.

b) y = x⁴ – 4x² + 2

Tập xác định của hàm số là R.

Ta có: y' = 4x³ – 8x = 4x(x² – 2)

y' = 0 $\Leftrightarrow$ $\Leftrightarrow$ x = 0 hoặc $x=-\sqrt{2}$ $x = - \sqrt{2}$ hoặc $x=\sqrt{2}$ $x = \sqrt{2}$

Lập bảng biến thiên của hàm số:

Từ bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại $x=-\sqrt{2}$ $x = - \sqrt{2}$ và y_CT = $y\left(-\sqrt{2}\right)$ $y (- \sqrt{2})$ = – 2

Hàm số đạt cực tiểu tại $x=\sqrt{2}$ $x = \sqrt{2}$ và y_CT = $y\left(\sqrt{2}\right)$ $y (\sqrt{2})$ = – 2

Hàm số đạt cực đại tại x = 0 và y_CĐ = y(0) = 2.

c) $y=\frac{x^2-2x+3}{x-1}$ $y = \frac{x^{2} - 2 x + 3}{x - 1}$

Tập xác định của hàm số là R \ {1}

Ta có: $y^{'} = \frac{(2 x - 2) (x - 1) - (x^{2} - 2 x + 3)}{{(x - 1)}^{2}} = \frac{x^{2} - 2 x - 1}{{(x - 1)}^{2}}$

y' = 0 $\Leftrightarrow$ $\Leftrightarrow$ $x=1-\sqrt{2}$ $x = 1 - \sqrt{2}$ hoặc $x=1+\sqrt{2}$ $x = 1 + \sqrt{2}$

Lập bảng biến thiên của hàm số:

Từ bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại $x=1+\sqrt{2}$ $x = 1 + \sqrt{2}$ và $y_{CT}=y\left(1+\sqrt{2}\right)=2\sqrt{2}$ $y_{C T} = y (1 + \sqrt{2}) = 2 \sqrt{2}$

Hàm số đạt cực đại tại $x=1-\sqrt{2}$ $x = 1 - \sqrt{2}$ và $y_{CĐ}=y\left(1-\sqrt{2}\right)=-2\sqrt{2}$ $y_{C Đ} = y (1 - \sqrt{2}) = - 2 \sqrt{2}$

d) $y=\sqrt{4x-2x^2}$ $y = \sqrt{4 x - 2 x^{2}}$

Tập xác định của hàm số là [0; 2]

Ta có: $y^{'} = \frac{4 - 4 x}{2 \sqrt{4 x - 2 x^{2}}} = \frac{2 - 2 x}{\sqrt{4 x - 2 x^{2}}}$

y' = 0 $\Leftrightarrow$ $\Leftrightarrow$ x = 1

Lập bảng biến thiên của hàm số:

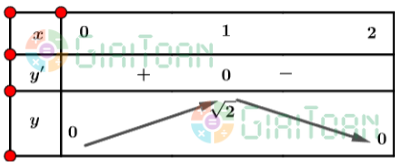
Từ bảng biến thiên, ta có:

Hàm số đạt cực đại tại x = 1 và $y_{CĐ}=y\left(1\right)=\sqrt{2}$ $y_{C Đ} = y (1) = \sqrt{2}$

Bài 1.8 trang 14 SGK Toán 12 tập 1 KNTT

Cho hàm số y = f(x) = |x|.

a) Tính các giới hạn $\lim_{x\rightarrow 0^+} \frac{f(x)-f(0)}{x-0}$ $lim_{x \to 0^{+}} \frac{f (x) - f (0)}{x - 0}$ và $\lim_{x\rightarrow 0^-} \frac{f(x)-f(0)}{x-0}$ $lim_{x \to 0^{-}} \frac{f (x) - f (0)}{x - 0}$ . Từ đó suy ra hàm số không có đạo hàm tại x = 0.

b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại x = 0 (xem Hình 1.4).

Hướng dẫn giải:

a) Ta có:

$\lim_{x\rightarrow 0^+} \frac{f(x)-f(0)}{x-0} =\frac{x-0}{x-0} =1$ $lim_{x \to 0^{+}} \frac{f (x) - f (0)}{x - 0} = \frac{x - 0}{x - 0} = 1$

$\lim_{x\rightarrow 0^+} \frac{f(x)-f(0)}{x-0} =\frac{-x-0}{x-0} =-1$ $lim_{x \to 0^{+}} \frac{f (x) - f (0)}{x - 0} = \frac{- x - 0}{x - 0} = - 1$

Do $\lim_{x\rightarrow 0^+} \frac{f(x)-f(0)}{x-0} \ne \lim_{x\rightarrow 0^-} \frac{f(x)-f(0)}{x-0}$ $lim_{x \to 0^{+}} \frac{f (x) - f (0)}{x - 0} \neq lim_{x \to 0^{-}} \frac{f (x) - f (0)}{x - 0}$ nên hàm số không có đạo hàm tại x = 0.

b) Do y' > 0 với mọi x ∈ (0; + ∞) và y' < 0 với mọi x ∈ (– ∞; 0) nên x = 0 là điểm cực tiểu của hàm số y = f(x).

Bài 1.9 trang 14 SGK Toán 12 tập 1 KNTT

Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số

$f\left(t\right)=\frac{5\ 000}{1+5e^{-t}},\ t\ \ge0,$ $f (t) = \frac{5 000}{1 + 5 e^{- t}}, t \geq 0,$

trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?

Hướng dẫn giải:

Đặt $g (x) = f^{'} (t) = \frac{5 000}{1 + 5 e^{- t}} = \frac{25 000 e^{- t}}{{(1 + 5 e^{- t})}^{2}}$

Ta có: $g^{'} (x) = \frac{- 25 000 e^{- t} (1 - 5 e^{- t})}{{(1 + 5 e^{- t})}^{3}}$

g'(x) = 0 $\Leftrightarrow$ $\Leftrightarrow$ t = ln5.

Ta có: g'(x) > 0 với mọi x ∈ [0; ln5) và g'(x) < 0 với mọi x ∈ (ln5; + ∞) nên hàm số g(x) đạt cực đại tại x = ln5.

Vậy sau t = ln5 thì tốc độ bán hàng là lớn nhất.

-----------------------------------------------

Bài tiếp theo: Toán 12 Kết nối tri thức bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Lời giải Toán 12 trang 14 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 1 Tính đơn điệu và cực trị của hàm số, được VnDoc biên soạn và đăng tải!

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

263

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!