Giải Toán 12 trang 59 tập 1 Kết nối tri thức
Giải Toán 12 trang 59 Tập 1
Giải Toán 12 trang 59 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 59.
Bài 2.9 trang 59 SGK Toán 12 tập 1 Kết nối
Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao.
Hướng dẫn giải:
Giả sử ba lực kéo trên mỗi sợi dây được biểu diễn bởi các vectơ 
\(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\) với O là đầu chung của ba sợi dây.
Khi các ba sợi dây ở trạng thái đứng yên thì \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)
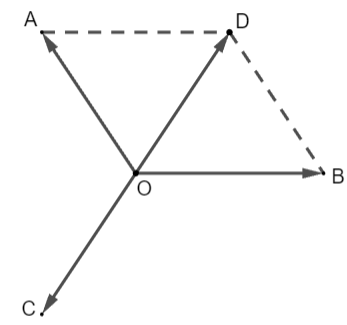
Vẽ điểm D sao cho OADB là hình bình hành \(\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OD}\)
Khi đó \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{0}\)
Suy ra \(\overrightarrow{OD}=-\overrightarrow{OC}\), hay O là trung điểm của CD.
Do đó O, A, B, C cùng thuộc mặt phẳng (ABCD)
Vậy ba sợi dây cùng nằm trong một mặt phẳng
Bài 2.10 trang 59 SGK Toán 12 tập 1 Kết nối
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:
a) \(\overrightarrow{AA'}\) và \(\overrightarrow{C'C}\)
b) \(\overrightarrow{AA'}\) và \(\overrightarrow{BC}\)
c) \(\overrightarrow{AC}\) và \(\overrightarrow{B'A'}\)
Hướng dẫn giải:
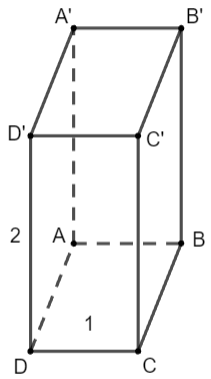
a) Vì ACC'A' là hình chữ nhật nên AA' = C'C và AA' // C'C
Hai vectơ \(\overrightarrow{AA'}\) và \(\overrightarrow{C'C}\) có cùng độ dài và ngược hướng nên \((\overrightarrow{AA'},\overrightarrow{C'C})=180^{\circ}\)
Vậy \(\overrightarrow{AA'}.\overrightarrow{C'C}=|\overrightarrow{AA'}|\cdot|\overrightarrow{C'C}|.\cos(\overrightarrow{AA'},\overrightarrow{C'C})\)
\(=2\cdot 2.\cos 180^{\circ} =-4\)
b) Vì ABCD là hình chữ nhật nên AD = BC và AD // BC
Hai vectơ \(\overrightarrow{AD}\) và \(\overrightarrow{BC}\) có cùng độ dài và cùng hướng nên \(\overrightarrow{AD}=\overrightarrow{BC}\)
Do đó \((\overrightarrow{AA'},\overrightarrow{BC})=(\overrightarrow{AA'},\overrightarrow{AD})=\widehat{A'AD}=90^{\circ}\)
Vậy \(\overrightarrow{AA'}.\overrightarrow{BC}=|\overrightarrow{AA'}|\cdot|\overrightarrow{BC}|.\cos(\overrightarrow{AA'},\overrightarrow{BC})\)
\(=|\overrightarrow{AA'}|\cdot|\overrightarrow{AD}|.\cos(\overrightarrow{AA'},\overrightarrow{AD})\)
\(=2\cdot 1.\cos 90^{\circ} =0\)
c) Vì ABB'A' là hình chữ nhật nên B'A' = BA và B'A' // BA
Hai vectơ \(\overrightarrow{B'A'}\) và \(\overrightarrow{BA}\) có cùng độ dài và cùng hướng nên \(\overrightarrow{B'A'}=\overrightarrow{BA}\)
Do đó \((\overrightarrow{AC},\overrightarrow{B'A'})=(\overrightarrow{AC},\overrightarrow{BA})=135^{\circ}\)
Vậy \(\overrightarrow{AC}.\overrightarrow{B'A'}=|\overrightarrow{AC}|\cdot|\overrightarrow{B'A'}|.\cos(\overrightarrow{AC},\overrightarrow{B'A'})\)
\(=|\overrightarrow{AC}|\cdot|\overrightarrow{BA}|.\cos(\overrightarrow{AC},\overrightarrow{BA})\)
\(=\sqrt{2} \cdot 1.\cos 135^{\circ} =-1\)
Bài 2.11 trang 59 SGK Toán 12 tập 1 Kết nối
Trong không gian, cho hai vectơ \(\vec{a}\) và \(\vec{b}\) cùng có độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là 45°, hãy tính:
a) \(\vec{a}\) . \(\vec{b}\)
b) \((\vec{a} +3\vec{b}). (\vec{a}-2\vec{b})\)
c) \((\vec{a} +\vec{b} )^{2}\)
Hướng dẫn giải:
a) \(\vec{a} .\vec{b}=|\vec{a}| .|\vec{b}|.\cos(\vec{a},\vec{b})\)
\(=1 .1.\cos45^{\circ} = \frac{\sqrt{2} }{2}\)
b) \((\vec{a} +3\vec{b}). (\vec{a}-2\vec{b}) = \vec{a}^2+\vec{a}\vec{b}-6\vec{b}^2\)
\(= |\vec{a}|^2+|\vec{a}||\vec{b}|.\cos(\vec{a},\vec{b})-6|\vec{b}|^2\)
\(= 1^2+\frac{\sqrt{2} }{2} -6.1^2\)
\(=\frac{-10+\sqrt{2}}{2}\)
c) \((\vec{a} +\vec{b} )^{2} =\vec{a}^2+2\vec{a}.\vec{b}+\vec{b}^2\)
\(=1^2+2.\frac{\sqrt{2} }{2} +1^2\)
\(=2+\sqrt{2}\)
Bài 2.12 trang 59 SGK Toán 12 tập 1 Kết nối
Cho tứ diện ABCD. Chứng minh rằng
a) \(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AC}.\overrightarrow{CD}+\overrightarrow{BC}.\overrightarrow{DC}\)
b) \(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\)
Hướng dẫn giải:
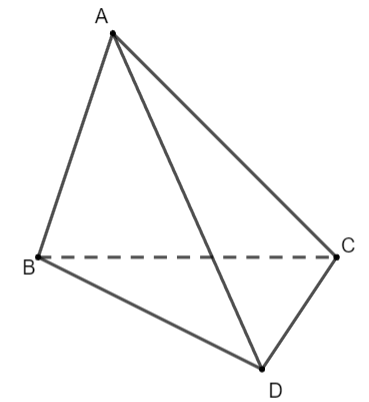
a) Ta có: \(\overrightarrow{AB}.\overrightarrow{CD}=(\overrightarrow{AC}+\overrightarrow{CB}).\overrightarrow{CD}\)
\(=\overrightarrow{AC}.\overrightarrow{CD}+\overrightarrow{CB}.\overrightarrow{CD}\)
\(=\overrightarrow{AC}.\overrightarrow{CD}+(-\overrightarrow{BC}).(-\overrightarrow{DC})\)
\(=\overrightarrow{AC}.\overrightarrow{CD}+\overrightarrow{BC}.\overrightarrow{DC}\)
b) Ta có: \(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}\)
\(=(\overrightarrow{AC}.\overrightarrow{CD}+\overrightarrow{BC}.\overrightarrow{DC})+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}\)
\(=(\overrightarrow{AC}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB})+(\overrightarrow{BC}.\overrightarrow{DC}+\overrightarrow{AD}.\overrightarrow{BC})\)
\(=\overrightarrow{AC}.(\overrightarrow{CD}+\overrightarrow{DB})+\overrightarrow{BC}.(\overrightarrow{DC}+\overrightarrow{AD})\)
\(=\overrightarrow{AC}.\overrightarrow{CB}+\overrightarrow{BC}.\overrightarrow{AC}\)
\(=\overrightarrow{AC}.(\overrightarrow{CB}+\overrightarrow{BC}) =0\)
-----------------------------------------------
---> Bài tiếp theo: Giải Toán 12 trang 60 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 59 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 6: Vectơ trong không gian, được VnDoc biên soạn và đăng tải!
