Giải Toán 12 trang 25 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 25 Tập 1
Giải Toán 12 trang 25 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 25.
Bài 4 trang 25 SGK Toán 12 tập 1 Chân trời
Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức 
\(y(t) = 5 - \frac{15t}{9t^{2}+1 }\) , với y được tính theo mg/l và t được tính theo giờ, t ≥ 0. Tìm các đường tiệm cận của đồ thị hàm số y = y(t). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn.
Hướng dẫn giải:
Xét hàm số \(y=y(t) = 5 - \frac{15t}{9t^{2}+1 } =\frac{45t^2-15t+5}{9t^{2}+1 }\)
TXĐ: \((0;+\infty)\)
Ta có: \(\lim_{t\rightarrow + \infty} y(t) =\lim_{t\rightarrow + \infty} \frac{45t^2-15t+5}{9t^{2}+1 } =5\)
Vậy đường thẳng y = 5 là tiệm cận ngang của đồ thị hàm số y = y(t).
NX: nồng độ oxygen trong hồ càng gần bằng 5mg/l khi thời gian t càng lớn.
Bài 5 trang 25 SGK Toán 12 tập 1 Chân trời
Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m=m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) trong Khởi động (trang 19).
Hướng dẫn giải:
Tập xác định: D = (0; c].
Ta có: \(\lim_{v\rightarrow 300\ 000^- } m(v) =\lim_{v\rightarrow 300\ 000^-} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{300\ 000^2}}}} }} = + \infty\)
Do đó v = 300 000 là tiệm cận đứng của đồ thị hàm số.
Hoạt động khám phá trang 25 SGK Toán 12 tập 1 Chân trời
Cho hàm số y = – x2 + 4x – 3.
a) Lập bảng biến thiên.
b) Vẽ đồ thị của hàm số.
Hướng dẫn giải:
a) Tập xác định: D = \(\mathbb{R}\).
Ta có: y' = - 2x + 4
y' = 0 ⇔ x = 2
Lập bảng biến thiên của hàm số:
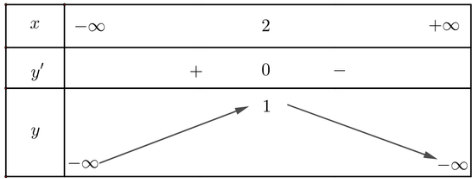
b) Giao điểm của đồ thị với trục Ox là hai điểm (1; 0) và (3; 0)
Giao điểm của đồ thị với trục Oy là điểm (- 3; 0)
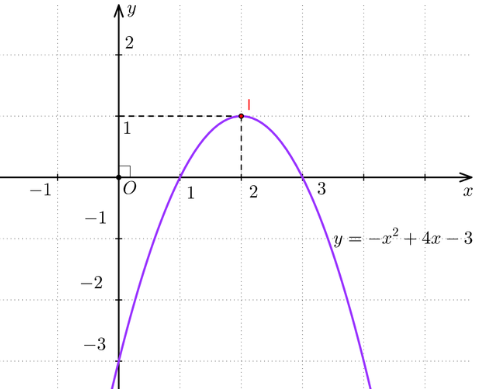
Hàm số y = – x2 + 4x – 3 có a = – 1 nên đồ thị hàm số là một parabol có bề lõm hướng xuống dưới, đỉnh I(2; 1):
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 28 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 25 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Đường tiệm cận của đồ thị hàm số và Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản, được VnDoc biên soạn và đăng tải!
