Giải Toán 12 trang 19 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 19 Tập 1
Giải Toán 12 trang 19 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 19.
Khám phá 1 trang 19 SGK Toán 12 tập 1 Chân trời
Cho hàm số 
\(y = \frac{1}{x-1}\) có đồ thị như Hình 1.
a) Tìm \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}},\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}}\)
b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi \(x \to {1^ + }\) và \(x \to {1^ - }\).
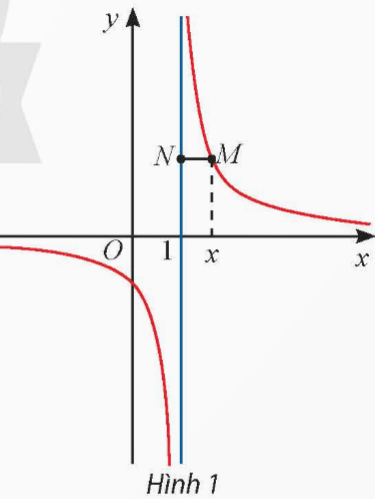
Hướng dẫn giải:
a) \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}} =+\infty\)
\(\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}} =-\infty\)
b) Từ đồ thị ta có: \(M\left(x;\frac{1}{x-1}\right)\) và \(N\left(1;\frac{1}{x-1}\right)\)
⇒ \(MN\left(1-x;0\right)\)
⇒ \(MN=\sqrt{\left(1-x\right)^2}=x-1\) (do x > 1)
Vậy khi \(x \to {1^ + }\) và \(x \to {1^ - }\) thì MN → 0.
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 20 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 19 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Đường tiệm cận của đồ thị hàm số, được VnDoc biên soạn và đăng tải!
