Giải Toán 12 trang 25 tập 1 Kết nối tri thức

Giải Toán 12 trang 25 Tập 1

Bài 1.16 trang 25 SGK Toán 12 tập 1 Kết nối
Bài 1.17 trang 25 SGK Toán 12 tập 1 Kết nối
Bài 1.18 trang 25 SGK Toán 12 tập 1 Kết nối
Bài 1.19 trang 25 SGK Toán 12 tập 1 Kết nối
Bài 1.20 trang 25 SGK Toán 12 tập 1 Kết nối

Giải Toán 12 trang 25 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 25.

Bài 1.16 trang 25 SGK Toán 12 tập 1 Kết nối

Hình 1.26 là đồ thị của hàm số $y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}$ $y = f (x) = \frac{2 x^{2}}{x^{2} - 1}$

Sử dụng đồ thị này, hãy:

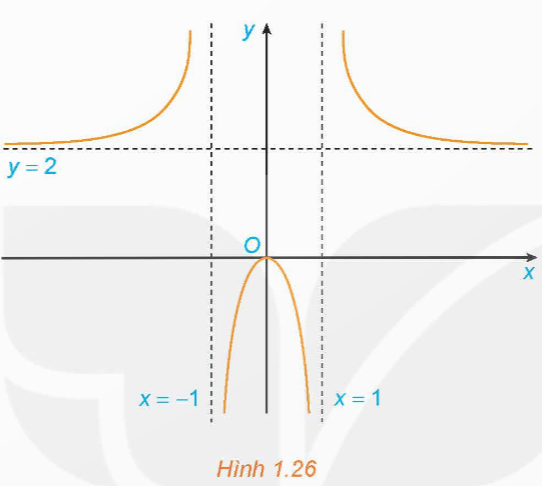
a) Viết kết quả của các giới hạn sau: $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right); \mathop {\lim }\limits_{x \to + \infty } f\left( x \right); \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right); \mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)$ $lim_{x \to - \infty} f (x); lim_{x \to + \infty} f (x); lim_{x \to 1^{-}} f (x); lim_{x \to - 1^{+}} f (x)$

b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Hướng dẫn giải:

a) Từ đồ thị ta có:

$\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2$ $lim_{x \to - \infty} f (x) = 2$ ; $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2$ $lim_{x \to + \infty} f (x) = 2$

$\mathop {\lim }\limits_{x \to 1^- } f\left( x \right) = -\infty$ $lim_{x \to 1^{-}} f (x) = - \infty$ ; $\mathop {\lim }\limits_{x \to - 1^+ } f\left( x \right) = -\infty$ $lim_{x \to - 1^{+}} f (x) = - \infty$

b) Đồ thị hàm số có:

Tiệm cận ngang: y = 2

Tiệm cận đứng: x = - 1 và x = 1.

Bài 1.17 trang 25 SGK Toán 12 tập 1 Kết nối

Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số $y = \frac{{{x^2} + 2x - 3}}{{x - 1}}$ $y = \frac{x^{2} + 2 x - 3}{x - 1}$ không?

Hướng dẫn giải:

Ta có: $\lim_{x\rightarrow 1^+} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \lim_{x\rightarrow 1^+} \frac{{(x-1)(x+3)}}{{x - 1}}$ $lim_{x \to 1^{+}} \frac{x^{2} + 2 x - 3}{x - 1} = lim_{x \to 1^{+}} \frac{(x - 1) (x + 3)}{x - 1}$

$= \lim_{x\rightarrow 1^+} (x+3)=4$ $= lim_{x \to 1^{+}} (x + 3) = 4$

$\lim_{x\rightarrow 1^-} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \lim_{x\rightarrow 1^-} \frac{{(x-1)(x+3)}}{{x - 1}}$ $lim_{x \to 1^{-}} \frac{x^{2} + 2 x - 3}{x - 1} = lim_{x \to 1^{-}} \frac{(x - 1) (x + 3)}{x - 1}$

$= \lim_{x\rightarrow 1^-} (x+3)=4$ $= lim_{x \to 1^{-}} (x + 3) = 4$

Vậy đường thẳng x = 1 không phải là tiệm cận đứng của đồ thị hàm số.

Bài 1.18 trang 25 SGK Toán 12 tập 1 Kết nối

Tìm các tiệm cận của đồ thị các hàm số sau:

a) $y = \frac{{3 - x}}{{2x + 1}}$ $y = \frac{3 - x}{2 x + 1}$ ;

b) $y = \frac{{2{x^2} + x - 1}}{{x + 2}}$ $y = \frac{2 x^{2} + x - 1}{x + 2}$ .

Hướng dẫn giải:

a) $y = f(x)= \frac{{3 - x}}{{2x + 1}}$ $y = f (x) = \frac{3 - x}{2 x + 1}$

Ta có: $\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{3 - x}}{{2x + 1}} =-\frac{1}{2}$ $lim_{x \to + \infty} f (x) = lim_{x \to + \infty} \frac{3 - x}{2 x + 1} = - \frac{1}{2}$ .

Tương tự $\lim_{x\rightarrow - \infty} f(x) =-\frac{1}{2}$ $lim_{x \to - \infty} f (x) = - \frac{1}{2}$

Vậy đồ thị hàm số f(x) có tiệm cận ngang là đường thẳng $y=-\frac{1}{2}$ $y = - \frac{1}{2}$ .

$\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^+ } f(x) =\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^+} \frac{{3 - x}}{{2x + 1}} = + \infty$ $lim_{x \to {(- \frac{1}{2})}^{+}} f (x) = lim_{x \to {(- \frac{1}{2})}^{+}} \frac{3 - x}{2 x + 1} = + \infty$ .

Tương tự $\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^- } f(x) = - \infty$ $lim_{x \to {(- \frac{1}{2})}^{-}} f (x) = - \infty$

Vậy đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng $x=-\frac{1}{2}$ $x = - \frac{1}{2}$ .

b) Ta có:

$\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{2{x^2} + x - 1}}{{x + 2}} = + \infty$ $lim_{x \to + \infty} f (x) = lim_{x \to + \infty} \frac{2 x^{2} + x - 1}{x + 2} = + \infty$ .

Tương tự $\lim_{x\rightarrow - \infty} f(x) =-\infty$ $lim_{x \to - \infty} f (x) = - \infty$

Vậy hàm số không có tiệm cận ngang.

$\lim_{x\rightarrow \left ( - 2\right ) ^+ } f(x) =\lim_{x\rightarrow \left ( - 2\right ) ^+} \frac{{2{x^2} + x - 1}}{{x + 2}} = + \infty$ $lim_{x \to {(- 2)}^{+}} f (x) = lim_{x \to {(- 2)}^{+}} \frac{2 x^{2} + x - 1}{x + 2} = + \infty$

Tương tự $\lim_{x\rightarrow \left ( - 2\right ) ^- } f(x) = - \infty$ $lim_{x \to {(- 2)}^{-}} f (x) = - \infty$

Vậy đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng x = - 2.

$f(x) = \frac{{2{x^2} + x - 1}}{{x + 2}} =(2x-3)+\frac{5}{x+2}$ $f (x) = \frac{2 x^{2} + x - 1}{x + 2} = (2 x - 3) + \frac{5}{x + 2}$

$\lim_{x\rightarrow + \infty} [f(x) - (2x - 3)] =\lim_{x\rightarrow + \infty} \frac{5}{x+2} =0$ $lim_{x \to + \infty} [f (x) - (2 x - 3)] = lim_{x \to + \infty} \frac{5}{x + 2} = 0$ .

Vậy đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = 2x - 3.

Bài 1.19 trang 25 SGK Toán 12 tập 1 Kết nối

Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là $C\left( x \right) = 2x + 50$ $C (x) = 2 x + 50$ (triệu đồng). Khi đó, $f\left( x \right) = \frac{{C\left( x \right)}}{x}$ $f (x) = \frac{C (x)}{x}$ là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2$ $lim_{x \to + \infty} f (x) = 2$ . Tính chất này nói lên điều gì?

Hướng dẫn giải:

Hàm số $f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2x+50}}{x}$ $f (x) = \frac{C (x)}{x} = \frac{2 x + 50}{x}$

Ta có: $f^{'} (x) = - \frac{50}{x^{2}}$ < 0 với mọi x khác 0. Do đó hàm số f(x) giảm.

$\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{2x+50}}{{x }} = 2$ $lim_{x \to + \infty} f (x) = lim_{x \to + \infty} \frac{2 x + 50}{x} = 2$

Tính chất này cho biết chi phí sản xuất trung bình cho mỗi sản phẩm ít nhất là 2 triệu đồng (nhưng không bằng 2)

Bài 1.20 trang 25 SGK Toán 12 tập 1 Kết nối

Một mảnh vườn hình chữ nhật có diện tích bằng 144 m². Biết độ dài một cạnh của mảnh vườn là x (m).

a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.

b) Tìm các tiệm cận của đồ thị hàm số P(x).

Hướng dẫn giải:

Độ dài cạnh còn lại của mảnh vườn là $\frac{144}{x}$ $\frac{144}{x}$ (m)

a) Biểu thức tính chu vi mảnh vườn là:

$P\left(x\right)=2\left(x+\frac{144}{x}\right) =2x+\frac{288}{x}$ $P (x) = 2 (x + \frac{144}{x}) = 2 x + \frac{288}{x}$ (m)

b) Ta có:

$\lim_{x\rightarrow + \infty} P(x) =\lim_{x\rightarrow + \infty} \left ( 2x+\frac{288}{x} \right ) = + \infty$ $lim_{x \to + \infty} P (x) = lim_{x \to + \infty} (2 x + \frac{288}{x}) = + \infty$

$\lim_{x\rightarrow - \infty} P(x) = - \infty$ $lim_{x \to - \infty} P (x) = - \infty$

Vậy hàm số không có tiệm cận ngang.

$\lim_{x\rightarrow 0 ^+ } P(x) =\lim_{x\rightarrow 0^+} \left ( 2x+\frac{288}{x} \right ) = + \infty$ $lim_{x \to 0^{+}} P (x) = lim_{x \to 0^{+}} (2 x + \frac{288}{x}) = + \infty$

Tương tự $\lim_{x\rightarrow 0 ^+ } P(x) = - \infty$ $lim_{x \to 0^{+}} P (x) = - \infty$

Vậy hàm số P(x) có tiệm cận đứng là đường thẳng x = 0.

$\lim_{x\rightarrow + \infty} [P(x) - (2x)] =\lim_{x\rightarrow + \infty} \frac{288}{x} =0$ $lim_{x \to + \infty} [P (x) - (2 x)] = lim_{x \to + \infty} \frac{288}{x} = 0$

Vậy đồ thị hàm số P(x) có tiệm cận xiên là đường thẳng y = 2x.

-----------------------------------------------

---> Bài tiếp theo: Toán 12 Kết nối tri thức bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Lời giải Toán 12 trang 25 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 3: Đường tiệm cận của đồ thị hàm số, được VnDoc biên soạn và đăng tải!

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

315

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!