Giải Toán 12 trang 5 tập 1 Cánh diều

Giải Toán 12 trang 5 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 5.

Hoạt động 1 trang 5 SGK Toán 12 tập 1 Cánh diều

a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng.

b) Cho hàm số y = f(x) = x² có đồ thị như Hình 2.

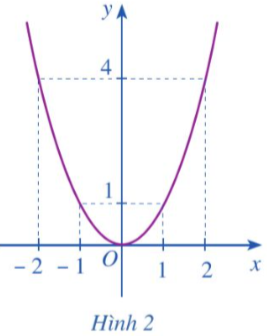
• Xác định khoảng đồng biến, nghịch biến của hàm số đó.
• Xét dấu của đạo hàm f'(x) = 2x.
• Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số f(x) = x² và dấu của đạo hàm f'(x) = 2x trên mỗi khoảng (– ∞; 0), (0; + ∞).
• Hoàn thành bảng biến thiên sau.

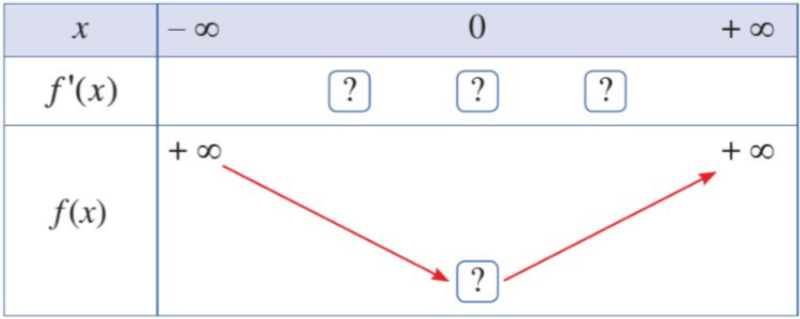
Hướng dẫn giải:

a) Cho hàm số y = f(x) xác định trên K.

+ Hàm số y = f(x) gọi là đồng biến trên K nếu ∀ x₁, x₂ thuộc K, x₁ < x₂ ⇒ f(x₁) < f(x₂).

+ Hàm số y = f(x) gọi là nghịch biến trên K nếu ∀ x₁, x₂ thuộc K, x₁ < x₂ ⇒ f(x₁) > f(x₂).

b) Từ đồ thị:

• Hàm số y = f(x) nghịch biến trên khoảng (– ∞; 0); đồng biến trên khoảng (0; + ∞).
• Ta có f'(x) = 2x > 0 với mọi x ∈ (0; + ∞) và f'(x) = 2x < 0 với mọi x ∈ (– ∞; 0).
• Mối liên hệ:

+ Ta có f'(x) < 0, hàm số f(x) nghịch biến trên khoảng (– ∞; 0)

+ Ta có f'(x) > 0, hàm số f(x) đồng biến trên khoảng (0; + ∞)

• Bảng biến thiên:

-----------------------------------------------

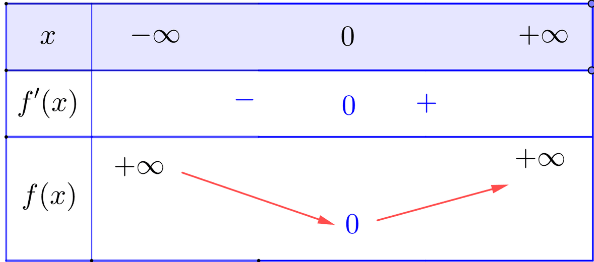
---> Xem thêm: Giải Toán 12 trang 6 tập 1 Cánh diều

Lời giải Toán 12 trang 5 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 1: Tính đơn điệu của hàm số, được VnDoc biên soạn và đăng tải!