Giải Toán 12 trang 92 tập 1 Cánh diều

Giải Toán 12 trang 92 Cánh diều Tập 1

Bài 1 trang 92 SGK Toán 12 tập 1
Bài 2 trang 92 SGK Toán 12 tập 1
Bài 3 trang 92 SGK Toán 12 tập 1

Giải Toán 12 trang 92 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 92.

Bài 1 trang 92 SGK Toán 12 tập 1

Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong Bảng 18.

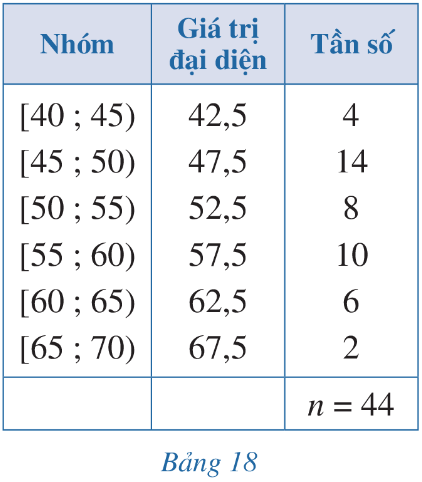
a) Phương sai của mẫu số liệu ghép nhóm trên là:

A. 53,2

B. 46,1

C. 30

D. 11

b) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:

A. 6,8

B. 7,3

C. 3,3

D. 46,1

Hướng dẫn giải:

a) Đáp án đúng: B

b) Đáp án đúng: A

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{4.42,5+14.47,5+8.52,5+10.57,5+6.62,5+2.67,5}{44}=\frac{585}{11}$ $\overset{―}{x} = \frac{4.42, 5 + 14.47, 5 + 8.52, 5 + 10.57, 5 + 6.62, 5 + 2.67, 5}{44} = \frac{585}{11}$

Phương sai của mẫu số liệu ghép nhóm là:

$s^2=\frac{1}{44}\left[4.\left(42,5-\frac{585}{11}\right)^2+14.\left(47,5-\frac{585}{11}\right)^2+8.\left(52,5-\frac{585}{11}\right)^2\right]$ $s^{2} = \frac{1}{44} [4. {(42, 5 - \frac{585}{11})}^{2} + 14. {(47, 5 - \frac{585}{11})}^{2} + 8. {(52, 5 - \frac{585}{11})}^{2}]$ $+\frac{1}{44}\left[10.\left(57,5-\frac{585}{11}\right)^2+6.\left(62,5-\frac{585}{11}\right)^2+2.\left(67,5-\frac{585}{11}\right)^2\right]\approx46,1$ $+ \frac{1}{44} [10. {(57, 5 - \frac{585}{11})}^{2} + 6. {(62, 5 - \frac{585}{11})}^{2} + 2. {(67, 5 - \frac{585}{11})}^{2}] \approx 46, 1$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $s=\sqrt{s^2}=\sqrt{46,1}\approx6,8$ $s = \sqrt{s^{2}} = \sqrt{46, 1} \approx 6, 8$

Bài 2 trang 92 SGK Toán 12 tập 1

Bảng 19, Bảng 20 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của hai công ty A, B (đơn vị: triệu đồng).

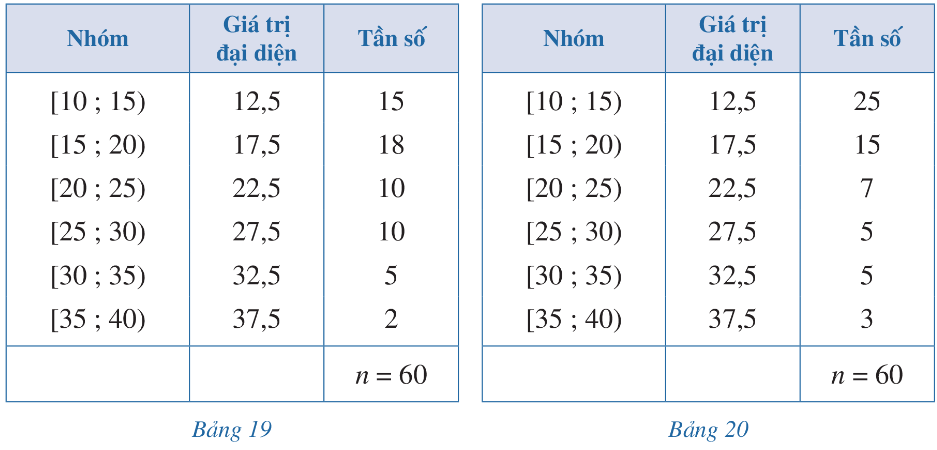
a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A, B.

b) Công ty nào có mức lương đồng đều hơn?

Hướng dẫn giải:

• Công ty A:

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{15.12,5+18.17,5+10.22,5+10.27,5+5.32,5+2.37,5}{60}=\frac{62}{3}$ $\overset{―}{x} = \frac{15.12, 5 + 18.17, 5 + 10.22, 5 + 10.27, 5 + 5.32, 5 + 2.37, 5}{60} = \frac{62}{3}$

Phương sai của mẫu số liệu ghép nhóm là:

$s^2=\frac{1}{60}\left[15.\left(12,5-\frac{62}{3}\right)^2+18.\left(17,5-\frac{62}{3}\right)^2+10.\left(22,5-\frac{62}{3}\right)^2\right]$ $s^{2} = \frac{1}{60} [15. {(12, 5 - \frac{62}{3})}^{2} + 18. {(17, 5 - \frac{62}{3})}^{2} + 10. {(22, 5 - \frac{62}{3})}^{2}]$ $+\frac{1}{60}\left[10.\left(27,5-\frac{62}{3}\right)^2+5.\left(32,5-\frac{62}{3}\right)^2+2.\left(37,5-\frac{62}{3}\right)^2\right]=\frac{1769}{36}$ $+ \frac{1}{60} [10. {(27, 5 - \frac{62}{3})}^{2} + 5. {(32, 5 - \frac{62}{3})}^{2} + 2. {(37, 5 - \frac{62}{3})}^{2}] = \frac{1769}{36}$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $s=\sqrt{s^2}=\sqrt{\frac{1769}{36}}\approx7$ $s = \sqrt{s^{2}} = \sqrt{\frac{1769}{36}} \approx 7$

• Công ty B:

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{25.12,5+15.17,5+7.22,5+5.27,5+5.32,5+3.37,5}{60}=\frac{229}{12}$ $\overset{―}{x} = \frac{25.12, 5 + 15.17, 5 + 7.22, 5 + 5.27, 5 + 5.32, 5 + 3.37, 5}{60} = \frac{229}{12}$

Phương sai của mẫu số liệu ghép nhóm là:

$s^2=\frac{1}{60}\left[25.\left(12,5-\frac{229}{12}\right)^2+15.\left(17,5-\frac{229}{12}\right)^2+7.\left(22,5-\frac{229}{12}\right)^2\right]$ $s^{2} = \frac{1}{60} [25. {(12, 5 - \frac{229}{12})}^{2} + 15. {(17, 5 - \frac{229}{12})}^{2} + 7. {(22, 5 - \frac{229}{12})}^{2}]$ $+\frac{1}{60}\left[5.\left(27,5-\frac{229}{12}\right)^2+5.\left(32,5-\frac{229}{12}\right)^2+3.\left(37,5-\frac{229}{12}\right)^2\right]=\frac{8339}{144}$ $+ \frac{1}{60} [5. {(27, 5 - \frac{229}{12})}^{2} + 5. {(32, 5 - \frac{229}{12})}^{2} + 3. {(37, 5 - \frac{229}{12})}^{2}] = \frac{8339}{144}$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $s=\sqrt{s^2}=\sqrt{\frac{8339}{144}}\approx7,61$ $s = \sqrt{s^{2}} = \sqrt{\frac{8339}{144}} \approx 7, 61$

b) Vì độ lệch chuẩn của mẫu số liệu ghép nhóm biểu diễn mức lương của công ty A nhỏ hơn độ lệch chuẩn của mẫu số liệu ghép nhóm biểu diễn mức lương của công ty B nên công ty A có mức lương đồng đều hơn.

Bài 3 trang 92 SGK Toán 12 tập 1

Bảng 21 biểu diễn mẫu số liệu ghép nhóm về tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

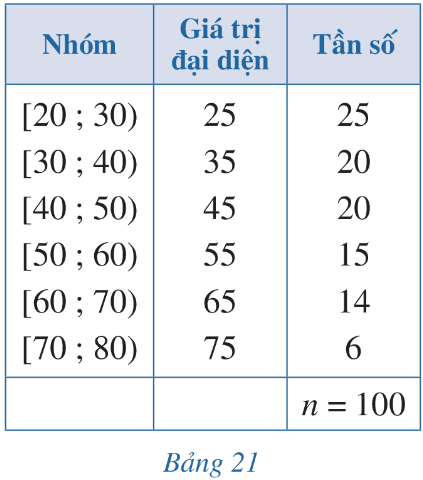
Hướng dẫn giải:

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{25.25+20.35+20.45+15.55+14.64+6.75}{100}=43,96$ $\overset{―}{x} = \frac{25.25 + 20.35 + 20.45 + 15.55 + 14.64 + 6.75}{100} = 43, 96$

Phương sai của mẫu số liệu ghép nhóm là:

$s^2=\frac{1}{100}\left[25.\left(25-44,1\right)^2+20.\left(35-44,1\right)^2+20.\left(45-44,1\right)^2\right]$ $s^{2} = \frac{1}{100} [25. {(25 - 44, 1)}^{2} + 20. {(35 - 44, 1)}^{2} + 20. {(45 - 44, 1)}^{2}]$

$+\frac{1}{100}\left[15.\left(55-44,1\right)^2+14.\left(65-44,1\right)^2+6.\left(75-44,1\right)^2\right]=244,19$ $+ \frac{1}{100} [15. {(55 - 44, 1)}^{2} + 14. {(65 - 44, 1)}^{2} + 6. {(75 - 44, 1)}^{2}] = 244, 19$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $s=\sqrt{s^2}=\sqrt{244,19}\approx15,63$ $s = \sqrt{s^{2}} = \sqrt{244, 19} \approx 15, 63$

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 93 tập 1 Cánh diều

Lời giải Toán 12 trang 92 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

63

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!