Giải Toán 12 trang 45 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 45 Tập 1
Giải Toán 12 trang 45 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 45.
Thực hành 3 trang 45 SGK Toán 12 tập 1 Chân trời
Cho hình hộp ABCD.EFGH. Thực hiện các phép toán sau đây:
a) 
\(\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{DH}\)
b) \(\overrightarrow{HE}+\overrightarrow{GC}+\overrightarrow{AB}\)
Hướng dẫn giải:
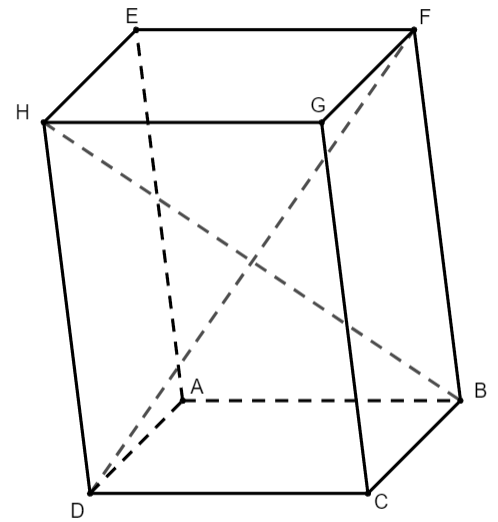
a) Theo quy tắc hình hộp, ta có: \(\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{DH}=\overrightarrow{DF}\)
b) Ta có: \(\overrightarrow{GC}=\overrightarrow{HD};\overrightarrow{AB}=\overrightarrow{HG}\)
Suy ra \(\overrightarrow{HE}+\overrightarrow{GC}+\overrightarrow{AB}=\overrightarrow{HE}+\overrightarrow{HD}+\overrightarrow{HG}\)
Theo quy tắc hình hộp, ta có: \(\overrightarrow{HE}+\overrightarrow{HD}+\overrightarrow{HG}=\overrightarrow{HB}\)
Vậy \(\overrightarrow{HE}+\overrightarrow{GC}+\overrightarrow{AB}=\overrightarrow{HB}\).
Hoạt động 4 trang 45 SGK Toán 12 tập 1 Chân trời
Cho hình hộp ABCD.A'B'C'D'.
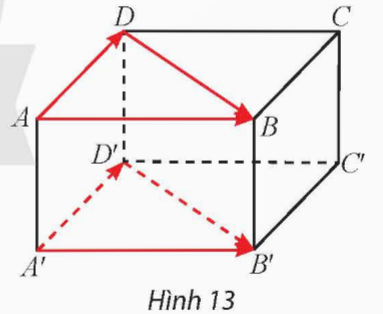
a) Trong mặt phẳng (ABCD), tìm vectơ hiệu \(\overrightarrow{AB}-\overrightarrow{AD}\).
Trong mặt phẳng (A'B'C'D'), tìm vectơ hiệu \(\overrightarrow {A'B'}- \overrightarrow {A'D'}\).
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow {AB}\) và \(\overrightarrow{A'B'},\overrightarrow{AD}\) và \(\overrightarrow{A'D'},\overrightarrow{DB}\) và \(\overrightarrow {D'B'}\).
c) Giải thích tại sao \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{A'B'}-\overrightarrow{A'D'}\)
Hướng dẫn giải:
a) Trong mặt phẳng (ABCD), \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}\)
Trong mặt phẳng (A'B'C'D'), \(\overrightarrow{A'B'}-\overrightarrow{A'D'}=\overrightarrow{D'B'}\)
b) Trong mp (ABB'A'): \(\overrightarrow{AB}=\overrightarrow{A'B'}\)
Trong mp (ADD'A'): \(\overrightarrow{AD}=\overrightarrow{A'D'}\)
Trong mp (BDD'B'): \(\overrightarrow{DB}=\overrightarrow{D'B'}\)
c) Ta có:
\(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}\) (câu a)
\(\overrightarrow{A'B'}-\overrightarrow{A'D'}=\overrightarrow{D'B'}\) (câu a)
\(\overrightarrow{DB}=\overrightarrow{D'B'}\) (câu b)
Vậy \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{A'B'}-\overrightarrow{A'D'}\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 46 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 45 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Vectơ và các phép toán trong không gian, được VnDoc biên soạn và đăng tải!
