Giải Toán 12 trang 22 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 22 Tập 1
Giải Toán 12 trang 22 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 22.
Hoạt động khám phá 3 trang 22 SGK Toán 12 tập 1 Chân trời
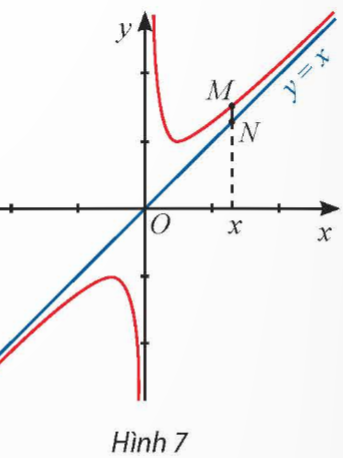
Cho đồ thị của hàm số 
\(y = \frac{x^{2} +1}{x}\) và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).
a) Tính \(\lim_{x\rightarrow -\infty } (\frac{x^{2}+1 }{x} -x)\) và \(\lim_{x\rightarrow +\infty } (\frac{x^{2}+1 }{x} -x)\)
b) Tính MN theo x và nhận xét về MN khi x → +∞ hoặc x → −∞.
Hướng dẫn giải:
a) \(\lim_{x\rightarrow-\infty}(\frac{x^2+1}{x}-x)=\lim_{x\rightarrow-\infty}\frac{1}{x}=0\)
\(\lim_{x\rightarrow+\infty}(\frac{x^2+1}{x}-x)=\lim_{x\rightarrow+\infty}\frac{1}{x}=0\)
b) \(M\left(x;\frac{x^2+1}{x}\right)\) và \(N\left(x;x\right)\)
\(\Rightarrow MN \left ( 0;-\frac{ 1}{x } \right ) \Rightarrow MN=\frac{ 1}{x }\)
Nhận xét: khi x → +∞ hoặc x → −∞ thì MN → 0.
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 24 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 22 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Đường tiệm cận của đồ thị hàm số, được VnDoc biên soạn và đăng tải!
