Giải Toán 12 trang 46 tập 1 Chân trời sáng tạo

Giải Toán 12 trang 46 Tập 1

Thực hành 4 trang 46 SGK Toán 12 tập 1 Chân trời
Thực hành 5 trang 46 SGK Toán 12 tập 1 Chân trời
Vận dụng 2 trang 46 SGK Toán 12 tập 1 Chân trời
Hoạt động 5 trang 46 SGK Toán 12 tập 1 Chân trời

Giải Toán 12 trang 46 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 46.

Thực hành 4 trang 46 SGK Toán 12 tập 1 Chân trời

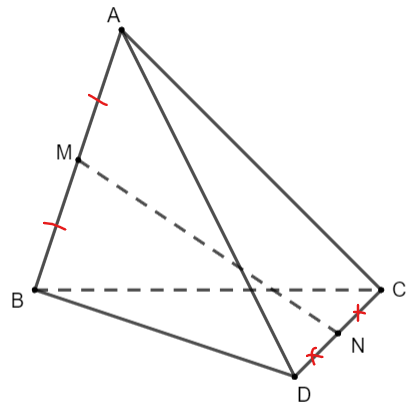
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ:

a) $\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{ND}$

b) $\overrightarrow{AD}-\overrightarrow{AM}+\overrightarrow{NC}$ .

Hướng dẫn giải:

a) Ta có: $\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{ND}$

$=\overrightarrow{BM}+\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NC}+\overrightarrow{ND}$

$=(\overrightarrow{BM}+\overrightarrow{AM})+\overrightarrow{MN}+(\overrightarrow{NC}+\overrightarrow{ND})$

$=\overrightarrow{MN}$

b) Ta có: $\overrightarrow{AD}-\overrightarrow{AM}+\overrightarrow{NC}$

$=\overrightarrow{MD}+\overrightarrow{NC}$

$=\overrightarrow{MN}+\overrightarrow{ND}+\overrightarrow{NC}$

$=\overrightarrow{MN}$

Thực hành 5 trang 46 SGK Toán 12 tập 1 Chân trời

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:

a) $\overrightarrow {a} = \overrightarrow {BA}+\overrightarrow {BC}+\overrightarrow {BB'}$

b) $\overrightarrow {b} = \overrightarrow {BC} - \overrightarrow {BA}+\overrightarrow {C'A}$

Hướng dẫn giải:

a) Ta có: $\overrightarrow{a}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BD'}$

Vậy $\left|\overrightarrow{a}\right|=\left|\overrightarrow{BD'}\right|=a\sqrt{3}$

b) Ta có: $\overrightarrow {b} = \overrightarrow {BC} - \overrightarrow {BA}+\overrightarrow {C'A}$

$=\overrightarrow{AC}+\overrightarrow{C'A}$

$=\overrightarrow{C'C}$

Vậy $\left|\overrightarrow{b}\right|=\left|\overrightarrow{C'C}\right|=a$

Vận dụng 2 trang 46 SGK Toán 12 tập 1 Chân trời

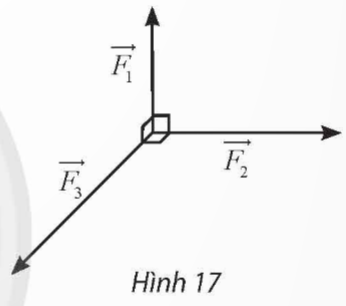
Ba lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2 N; 3 N; 4 N (Hình 17). Tính độ lớn hợp lực của ba lực đã cho.

Hướng dẫn giải:

Hợp lực $\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}$

Độ lớn hợp lực của ba lực đã cho là:

$F=\sqrt{2^2+3^2+4^2}=\sqrt{29}$ (N)

Hoạt động 5 trang 46 SGK Toán 12 tập 1 Chân trời

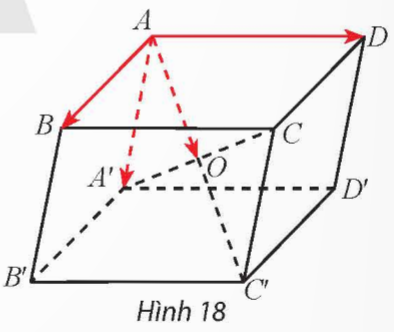
Cho hình hộp ABCD.A'B'C'D' có AC' và A'C cắt nhau tại O (Hình 18).

a) Tìm vectơ $\overrightarrow {AB}+\overrightarrow {AD}+\overrightarrow {AA'}$ .

b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a và vectơ $\overrightarrow {AO}$ .

Hướng dẫn giải:

a) Áp dụng quy tắc hình hộp, ta có: $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}$

b) Ta có: $\overrightarrow{AC'}=2\overrightarrow{AO}$

Do đó $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=2\overrightarrow{AO}$

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 47 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 46 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Vectơ và các phép toán trong không gian, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

Bài trước

Bài sau