Giải Toán 12 trang 40 tập 1 Kết nối tri thức
Giải Toán 12 trang 40 Tập 1
Giải Toán 12 trang 40 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 40.
Vận dụng trang 40 SGK Toán 12 tập 1 Kết nối
Một nhà sản xuất trung bình bán được 1 000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?
c) Nếu hàm chi phí hằng tuần là C(x) = 12 000 – 3x (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
Hướng dẫn giải:
a) Gọi p (triệu đồng) là giá của mỗi chiếc ti vi; x là số người mua ti vi.
Theo giả thiết, tốc độ thay đổi của x tỉ lệ với tốc độ thay đổi của p nên hàm số p = p(x) là hàm số bậc nhất.
Giá ti vi p1 = 14 ứng với x1 = 1 000 và giá ti vi p2 = 13,5 ứng với x2 = 1 100.
Do đó, phương trình đường thẳng p = ax + b đi qua hai điểm (1 000; 14) và (1 100; 13,5).
Suy ra hàm cầu 
\(p\left(x\right)=-\frac{1}{200}x+19\)
b) Ta có: \(p =-\frac{1}{200}x+19\) nên x = – 200p + 3 800.
Hàm doanh thu là:
R(x) = px = p(– 200p + 3 800) = – 200p2 + 3 800p
R'(x) = – 400p + 3 800; R'(x) = 0 ⇔ p = 9,5
Bảng biến thiên:
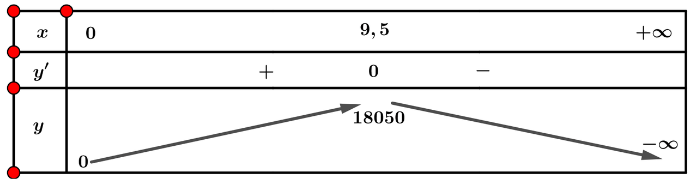
Vậy công ty nên giảm giá 14 – 9,5 = 4,5 triệu đồng mỗi chiếc thì doanh thu lớn nhất.
c) Hàm số biểu thị doanh thu bán hàng x sản phẩm là:
\(R(x)=px=x\left(-\frac{1}{200}x+19\right)=-\frac{1}{200}x^2+19x\) (triệu đồng)
Hàm số biểu thị lợi nhuận của công ty là:
\(P(x)= \left ( -\frac{1}{200}x^2+19x \right ) - \left (12\ 000\ -\ 3x \right )\)
\(=-\frac{1}{200}x^2+22x-12\ 000\) (triệu đồng)
Ta có: \(P'(x)=-\frac{x}{100}+22, \ P'(x)=0\Leftrightarrow x =2\ 200\)
Bảng biến thiên:
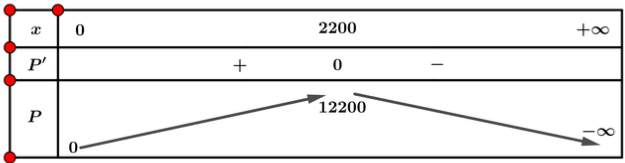
Vậy cửa hàng nên đặt giá bán là \(p=-\frac{1}{200}.2200+19=8\) triệu đồng thì lợi nhuận cao nhất.
Bài 1.26 trang 40 SGK Toán 12 tập 1 Kết nối
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t (giây) là y = t3 – 12t + 3, t ≥ 0.
a) Tìm các hàm vận tốc và gia tốc.
b) Khi nào thì hạt chuyển động lên trên và khi nào thì hạt chuyển động xuống dưới.
c) Tìm quãng đường hạt đi được trong khoảng thời gian 0 ≤ t ≤ 3.
d) Khi nào hạt tăng tốc? khi nào hạt giảm tốc?
Hướng dẫn giải:
a) Ta có:
Hàm vận tốc là: v(t) = y' = 3t2 – 12 với t ≥ 0
Hàm gia tốc là: a(t) = y'' = 6t với t ≥ 0
b) Bảng xét dấu:
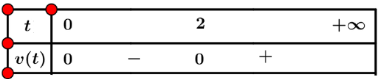
Hạt chuyển động lên trên khi v(t) > 0 ⇔ t > 2
Hạt chuyển động xuống dưới khi v(t) < 0 ⇔ 0 < t < 2
c) Ta có: y(3) – y(0) = – 9
=> Quãng đường vật đi được trong thời gian 0 ≤ t ≤ 3 là: 9 m.
d) Với mọi t ≥ 0, ta có a(t) = 6t ≥ 0
Vậy hạt tăng tốc khi t > 0.
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 41 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 40 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn, được VnDoc biên soạn và đăng tải!
