Giải Toán 12 trang 50 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 50 Tập 1
Giải Toán 12 trang 50 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 50.
Thực hành 8 trang 50 SGK Toán 12 tập 1 Chân trời
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1.
a) Tính các tích vô hướng: 
\(\overrightarrow{AB}.\overrightarrow{A'C'},\overrightarrow{AB}.\overrightarrow{CC'}\)
b) Tính góc \((\overrightarrow{AC}.\overrightarrow{AC'})\) (kết quả làm tròn đến phút).
Hướng dẫn giải:
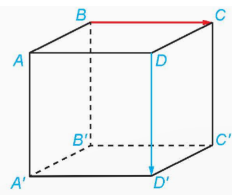
a) Ta có:
\(\overrightarrow{AB}\cdot\overrightarrow{A'C'}=|\overrightarrow{AB}|\cdot|\overrightarrow{A'C'}|\cdot\cos(\overrightarrow{AB},\overrightarrow{A'C'})\)
\(=|\overrightarrow{AB}|\cdot|\overrightarrow{A'C'}|\cdot\cos(\overrightarrow{AB},\overrightarrow{AC})\)
\(=1\cdot\sqrt{2}\cdot\cos45^{\circ}=1\)
Do \(\overrightarrow{CC'}=\overrightarrow{BB'}\), nên:
\(\overrightarrow{AB}\cdot\overrightarrow{CC'}=\overrightarrow{AB}\cdot\overrightarrow{BB'}\)
\(=|\overrightarrow{AB}|\cdot|\overrightarrow{BB'}|\cdot\cos(\overrightarrow{AB},\overrightarrow{BB'})\)
\(=1\cdot1\cdot\cos90^{\circ}=0\)
b) \(\overrightarrow{AC}.\overrightarrow{AC'}=\overrightarrow{AC}.\left(\overrightarrow{AC}+\overrightarrow{CC'}\right)\)
\(=AC^2+\overrightarrow{AC}.\overrightarrow{CC'}=2\)
Vậy \(\cos\left(\overrightarrow{AC}.\overrightarrow{AC'}\right)=\frac{\overrightarrow{AC}.\overrightarrow{AC'}}{|\overrightarrow{AC}|.|\overrightarrow{AC'}|}=\frac{2}{\sqrt{2}.\sqrt{3}}=\frac{2}{\sqrt{6}}\)
Suy ra \((\overrightarrow{AC}.\overrightarrow{AC'})\) ≈ 35o 15'
Vận dụng 4 trang 50 SGK Toán 12 tập 1 Chân trời
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30o (Hình 27).
a) Tính độ lớn của trọng lực \(\overrightarrow{P}=m\overrightarrow{g\ }\) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g\) có độ lớn 9,8 m/s2.
b) Cho biết công A (J) sinh bởi một lực \(\overrightarrow{F\ }\) có độ dịch chuyển \(\overrightarrow{d\ }\) được tính bởi công thức \(A=\overrightarrow{F}.\overrightarrow{d\ }\). Hãy tính công sinh bởi trọng lực \(\overrightarrow{P\ }\) khi em nhỏ trượt hết chiều dài cầu trượt.
Hướng dẫn giải:
a) Trong lực P = m . g = 25 . 9,8 = 245 N
b) Công sinh bởi trọng lực \(\overrightarrow{P\ }\) khi em nhỏ trượt hết chiều dài cầu trượt là:
\(A=\left|\overrightarrow{P}\right|.\left|\overrightarrow{d\ }\right|.\cos\left(\overrightarrow{P},\overrightarrow{d\ }\right)\) = 245 . 3,5 . cos 60o = 428,75 (J)
Bài 1 trang 50 SGK Toán 12 tập 1 Chân trời
Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'}\)
b) \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'}\)
c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0\)
Hướng dẫn giải:
a) Ta có: \(\overrightarrow{B'C'}=\overrightarrow{AD};\ \overrightarrow{DD'}=\overrightarrow{AA'}\)
Áp dụng quy tắc hình hộp, ta có:
\(\overrightarrow{AB}+\overrightarrow{B'C'}+\overrightarrow{DD'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)
b) Ta có: \(\overrightarrow{DB'}+\overrightarrow{D'D}+\overrightarrow{BD'}\)
\(=\overrightarrow{DB'}+\left(\overrightarrow{BD'}+\overrightarrow{D'D}\right)\)
\(=\overrightarrow{DB'}+\overrightarrow{BD}=\overrightarrow{BB'}\)
c) \(\overrightarrow{AC}+\overrightarrow{BA'}+\overrightarrow{DB}+\overrightarrow{C'D}\)
\(=\overrightarrow{AC}+\left(\overrightarrow{C'D}+\overrightarrow{DB}+\overrightarrow{BA'}\right)\)
\(=\overrightarrow{A'C'}+\overrightarrow{C'A'}=\overrightarrow{0\ }\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 51 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 50 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Vectơ và các phép toán trong không gian, được VnDoc biên soạn và đăng tải!
