VnDoc.com

Toán 12 Chân trời sáng tạo bài 3: Biểu thức toạ độ của các phép toán vectơ

Bài trước

Bài sau

Giải bài tập Toán 12 CTST bài 3

Giải Toán 12 trang 58 Chân trời
- Hoạt động khởi động trang 58 SGK Toán 12 tập 1
- Hoạt động khám phá 1 trang 58 SGK Toán 12 tập 1
Giải Toán 12 trang 59 Chân trời
Giải Toán 12 trang 60 Chân trời
Giải Toán 12 trang 61 Chân trời
- Thực hành 3 trang 61 SGK Toán 12 tập 1
- Hoạt động khám phá 4 trang 61 SGK Toán 12 tập 1
Giải Toán 12 trang 62 Chân trời
- Thực hành 4 trang 62 SGK Toán 12 tập 1
- Vận dụng 3 trang 62 SGK Toán 12 tập 1
Giải Toán 12 trang 63 Chân trời
- Thực hành 5 trang 63 SGK Toán 12 tập 1
Giải Toán 12 trang 64 Chân trời

Toán 12 Chân trời sáng tạo bài 3: Biểu thức toạ độ của các phép toán vectơ được VnDoc.com tổng hợp với hướng dẫn giải bài tập SGK Toán 12 Chân trời sáng tạo tập 1 các trang 58, 59, 60, 61, 62, 63, 64.

Giải Toán 12 trang 58 Chân trời

Hoạt động khởi động trang 58 SGK Toán 12 tập 1

Trong không gian Oxyz, có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trong mặt phẳng Oxy không?

$\overrightarrow {a}$ $\overrightarrow {a}$ = (x;y;z), $\overrightarrow {a$ $\overrightarrow {a'}$ = (x';y';z')

$\overrightarrow {a} + \overrightarrow {a$ $\overrightarrow {a} + \overrightarrow {a'} = ?$

Hoạt động khám phá 1 trang 58 SGK Toán 12 tập 1

Trong không gian Oxyz, cho hai vectơ $\overrightarrow a = ({a_1};{a_2};{a_3})$ $\overrightarrow a = ({a_1};{a_2};{a_3})$, và $\overrightarrow b = ({b_1};{b_2};{b_3})$ $\overrightarrow b = ({b_1};{b_2};{b_3})$ số m.

a) Biểu diễn từng vectơ $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ theo ba vectơ $\overrightarrow i ,\overrightarrow j ,\overrightarrow k$ $\overrightarrow i ,\overrightarrow j ,\overrightarrow k$

b) Biểu diễn các vectơ $\overrightarrow a + \overrightarrow b , \overrightarrow a - \overrightarrow b , m\overrightarrow a$ $\overrightarrow a + \overrightarrow b , \overrightarrow a - \overrightarrow b , m\overrightarrow a$ theo ba vectơ $\overrightarrow i ,\overrightarrow j ,\overrightarrow k$ $\overrightarrow i ,\overrightarrow j ,\overrightarrow k$, từ đó suy ra toạ độ của các vectơ $\overrightarrow a + \overrightarrow b , \overrightarrow a - \overrightarrow b , m\overrightarrow a$ $\overrightarrow a + \overrightarrow b , \overrightarrow a - \overrightarrow b , m\overrightarrow a$

Xem lời giải Toán 12 trang 58

Giải Toán 12 trang 59 Chân trời

Thực hành 1 trang 59 SGK Toán 12 tập 1

Cho ba vectơ $\overrightarrow a = (2; - 5;3), \overrightarrow b = (0;2; - 1), \overrightarrow b = (1;7;2)$ $\overrightarrow a = (2; - 5;3), \overrightarrow b = (0;2; - 1), \overrightarrow b = (1;7;2)$

a) Tìm toạ độ của vectơ $\overrightarrow d = 4\overrightarrow a - \frac{1}{3}\overrightarrow b + 3\overrightarrow c$ $\overrightarrow d = 4\overrightarrow a - \frac{1}{3}\overrightarrow b + 3\overrightarrow c$

b) Tìm toạ độ của vectơ $\overrightarrow e = \overrightarrow a - 4\overrightarrow b - 2\overrightarrow c$ $\overrightarrow e = \overrightarrow a - 4\overrightarrow b - 2\overrightarrow c$

c) Chứng minh $\overrightarrow a$ $\overrightarrow a$ cùng phương với vectơ $\overrightarrow m = ( - 6;15; - 9)$ $\overrightarrow m = ( - 6;15; - 9)$

Vận dụng 1 trang 59 SGK Toán 12 tập 1

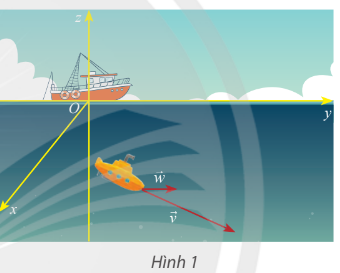
Một thiết bị thăm dò đáy biển đang lặn với vận tốc $\overrightarrow v = (10;8; - 3)$ $\overrightarrow v = (10;8; - 3)$ (Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là $\overrightarrow w = (3,5;1;0)$ $\overrightarrow w = (3,5;1;0)$

a) Tìm toạ độ của vectơ tổng hai vận tốc $\overrightarrow v và \overrightarrow w$ $\overrightarrow v và \overrightarrow w$

b) Giả sử thiết bị thăm dò lặn với vận tốc $\overrightarrow u = (7;2;0)$ $\overrightarrow u = (7;2;0)$, hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.

Giải Toán 12 trang 59 Chân trời

Hoạt động khám phá 2 trang 59 SGK Toán 12 tập 1

Cho hai vectơ $\overrightarrow a = ({a_1};{a_2};{a_3}), \overrightarrow b = ({b_1};{b_2};{b_3})$ $\overrightarrow a = ({a_1};{a_2};{a_3}), \overrightarrow b = ({b_1};{b_2};{b_3})$.

a) Biểu diễn từng vectơ $\overrightarrow a và \overrightarrow b$ $\overrightarrow a và \overrightarrow b$ theo ba vectơ $\overrightarrow i ,\overrightarrow j ,\overrightarrow k$ $\overrightarrow i ,\overrightarrow j ,\overrightarrow k$

b) Tính các tích vô hướng ${\overrightarrow i ^2},{\overrightarrow j ^2},{\overrightarrow k ^2}, \overrightarrow i .\overrightarrow j , \overrightarrow j .\overrightarrow k , \overrightarrow k .\overrightarrow i$ ${\overrightarrow i ^2},{\overrightarrow j ^2},{\overrightarrow k ^2}, \overrightarrow i .\overrightarrow j , \overrightarrow j .\overrightarrow k , \overrightarrow k .\overrightarrow i$

c) Tính tích vô hướng $\overrightarrow a .\overrightarrow b$ $\overrightarrow a .\overrightarrow b$ theo toạ độ của hai vectơ $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$

Xem lời giải Toán 12 trang 59

Giải Toán 12 trang 60 Chân trời

Thực hành 2 trang 60 SGK Toán 12 tập 1

Cho ba vectơ $\overrightarrow m = ( - 5;4;9), \overrightarrow n = (2; - 7;0), \overrightarrow p = (6;3; - 4)$ $\overrightarrow m = ( - 5;4;9), \overrightarrow n = (2; - 7;0), \overrightarrow p = (6;3; - 4)$.

a) Tính $\overrightarrow m .\overrightarrow n , \overrightarrow m .\overrightarrow p$ $\overrightarrow m .\overrightarrow n , \overrightarrow m .\overrightarrow p$

c) Cho $\overrightarrow q = (1; - 2;0)$ $\overrightarrow q = (1; - 2;0)$. Vectơ $\overrightarrow q$ $\overrightarrow q$ có vuông góc với $\overrightarrow p$ $\overrightarrow p$ không?

Vận dụng 2 trang 60 SGK Toán 12 tập 1

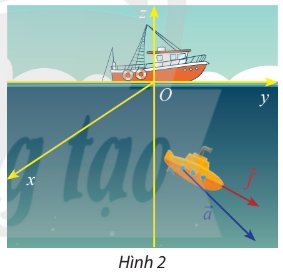
Một thiết bị thăm dò đáy biển (Hình 2) được đẩy bởi một lực $\overrightarrow f = (5;4; - 2)$ $\overrightarrow f = (5;4; - 2)$ (đơn vị: N) giúp thiết bị thực hiện độ dời $\overrightarrow a = (70;20; - 40)$ $\overrightarrow a = (70;20; - 40)$ (đơn vị: m). Tính công sinh bởi lực $\overrightarrow f$ $\overrightarrow f$

Giải Toán 12 trang 60 Chân trời

Hoạt động khám phá 3 trang 60 SGK Toán 12 tập 1

Cho hai điểm $A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})$ $A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})$. Từ biểu thức $\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA}$ $\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA}$, tìm toạ độ của vectơ $\overrightarrow {AB}$ $\overrightarrow {AB}$ theo toạ độ hai điểm A, B.

Xem lời giải Toán 12 trang 60

Giải Toán 12 trang 61 Chân trời

Thực hành 3 trang 61 SGK Toán 12 tập 1

Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).

a) Tìm toạ độ của các vectơ $\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP}$ $\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP}$

b) Tính các độ dài MN, NP, MP.

Hoạt động khám phá 4 trang 61 SGK Toán 12 tập 1

Cho tam giác ABC có $A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})$ $A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})$. Gọi $M({x_M};{y_M};{z_M})$ $M({x_M};{y_M};{z_M})$ là trung điểm của đoạn thẳng AB và $G({x_G};{y_G};{z_G})$ $G({x_G};{y_G};{z_G})$ là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ $\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} ),\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )$ $\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} ),\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )$, tìm toạ độ của các điểm M và G.

Xem lời giải Toán 12 trang 61

Giải Toán 12 trang 62 Chân trời

Thực hành 4 trang 62 SGK Toán 12 tập 1

Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:

a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;

b) Trọng tâm G của tam giác M′N′P′.

Vận dụng 3 trang 62 SGK Toán 12 tập 1

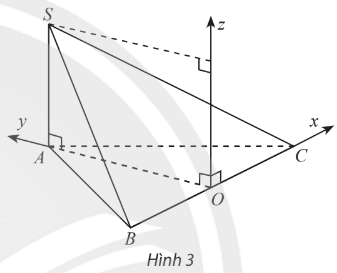
Cho hình chóp S.ABC có $SA \bot (ABC)$ $SA \bot (ABC)$, SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:

a) Các điểm A, S, B, C

b) Trung điểm M của SB và trung điểm N của SC;

c) Trọng tâm G của tam giác SBC

Giải Toán 12 trang 62 Chân trời

Xem lời giải Toán 12 trang 62

Giải Toán 12 trang 63 Chân trời

Thực hành 5 trang 63 SGK Toán 12 tập 1

Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).

a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.

b) Tìm độ dài cạnh MN và MP.

c) Tính góc M

Xem lời giải Toán 12 trang 63

Giải Toán 12 trang 64 Chân trời

Vận dụng 4 trang 64 SGK Toán 12 tập 1

Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:

a) Các khoảng cách giữa mỗi cặp drone giao hàng.

b) Góc $\widehat {BAC}$ $\widehat {BAC}$

Bài 1 trang 64 SGK Toán 12 tập 1

Cho hai vectơ $\overrightarrow a = ({a_1};{a_2};{a_3}), \overrightarrow b = ({b_1};{b_2};{b_3})$ $\overrightarrow a = ({a_1};{a_2};{a_3}), \overrightarrow b = ({b_1};{b_2};{b_3})$, ta có biểu thức tọa độ của tích vô hướng $\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}$ $\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}$

Bài 2 trang 64 SGK Toán 12 tập 1

Cho hai vectơ $\overrightarrow a$ $\overrightarrow a$ = (0; 1; 3) và $\overrightarrow b$ $\overrightarrow b$ = (–2; 3; 1). Tìm toạ độ của vectơ $2\overrightarrow b - \frac{3}{2}\overrightarrow a$ $2\overrightarrow b - \frac{3}{2}\overrightarrow a$

Bài 3 trang 64 SGK Toán 12 tập 1

Cho ba điểm A(2; 1; –1), B(3; 2; 0) và C(2; –1; 3).

a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.

b) Tìm toạ độ trung điểm của các cạnh của tam giác ABC.

c) Tìm toạ độ trọng tâm G của tam giác ABC.

Bài 4 trang 64 SGK Toán 12 tập 1

Cho điểm M(1; 2; 3). Hãy tìm toạ độ của các điểm:

a) M₁, M₂, M₃ lần lượt là hình chiếu vuông góc của M trên các mặt phẳng toạ độ (Oxy), (Oyz), (Oxz).

b) Gọi M', M", M"' lần lượt là các điểm thỏa mãn:

• O là trung điểm của MM';

• MM" vuông góc với mặt phẳng (Oxy) tại điểm H sao cho H là trung điểm của MM".

• MM"' vuông góc và cắt trục Oy tại điểm K sao cho K là trung điểm của MM"'.

Bài 5 trang 64 SGK Toán 12 tập 1

Cho ba điểm A(3; 3; 3), B(1; 1; 2) và C(5; 3; 1).

a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.

b) Tìm điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.

Bài 6 trang 64 SGK Toán 12 tập 1

Cho các điểm A(–1; –1; 0), B(0; 3; –1), C(–1; 14; 0), D(–3; 6; 2). Chứng minh rằng ABCD là hình thang.

Bài 7 trang 64 SGK Toán 12 tập 1

Cho hình hộp ABCD.A'B'C'D' có A(1; 0; 1), B(2; 1; 2), D(1; −1; 1), C'(4; 5; −5). Tìm tọa độ các đỉnh còn lại của hình hộp.

Bài 8 trang 64 SGK Toán 12 tập 1

Tính công sinh bởi lực $\overrightarrow F$ $\overrightarrow F$= (20; 30; –10) (đơn vị: N) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển $\overrightarrow d$ $\overrightarrow d$ = (150; 200; 100) (đơn vị: m).

Giải Toán 12 trang 64 Chân trời